
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Звуковая мощность источника звука, направленность излучения, фактор направленности. Сферический и цилиндрический источники звука.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Акустические характеристики звука: высота тона, тембр, акустические гармоники и акустические спектры (дискретные, сплошные, комбинированные). Октава, третьоктавы среднегеометрическая частота. Диапазон частот, принятый для анализа. Звуковые колебания прежде всего различаются по частоте. Частота звука определяет высоту тона: чем выше частота, тем выше тон. Чистый тон - это звуковое колебание с одним и тем же числом колебаний в секунду. Они создаются, например, камертоном. Однако большинство звуков представляют набор частот, т.е. имеем дело со сложным звуком, но тем не менее любой сложный колебательный процесс может быть разложен на простейшие гармонические колебательные процессы, как это и следует из уравнения Фурье, согласно которому любая функция может быть представлена как сумма конечного или бесконечного числа простейших, гармонических функций (изменяющихся по закону синуса или косинуса). Операция разложения сложного колебательного процесса на простейшие составляющие называют частотным анализом, а величины, характеризующие распределение энергии по частотному диапазону - его частотным акустическим спектром. Акустический спектр можно получить на экране осциллографа, но мы не можем судить по его картинке о составе звука. Спектр можно представить в виде диаграммы, на которой по оси абсцисс откладываются частоты, а по оси ординат энергия на соответствующей частоте (или относительная доля энергии от общей энергии), звуковая мощность, звуковое давление или уровни звука по полосам частот. Спектры процессов, которые могут быть представлены в виде ограниченного количества чистых тонов(синусоидальных звуков) называют дискретными или линейчатыми (рис. 2 стр. 7 посмотреть). (ƒ фи наклонная) Спектры случайных или непериодических процессов, к которым относятся шумы различных машин, называются сплошным (рис. 3) и поэтому нужно говорить о ширине полосы спектра - его нижней граничной частоте (f H) и верхней частоте (f В). За среднюю частоту полосы принимается среднегеометрическая частота (f cp). Спектры широкополосных акустических сигналов представляют в виде набора среднегеометрических частот: f cp= Существует еще одна разновидность акустических спектров - сплошные спектры с наличием в них дискретных составляющих. Их создают, например, осевые вентиляторы, имеющие несколько дискретных частот, низшая из которых определяется числом лопастей и скоростью вращения. В музыкальной акустике дискретный спектр звуков, создаваемых инструментами, характеризует тембр звука - специфический оттенок звучания инструмента. Он состоит из обертонов и основного тона. Основной тон соответствует наименьшей частоте, присутствующей в сложном звуке; первый обертон - частоте в 2 раза большей основного тона; второй обертон - в 3 раза и т.д. Тембр звука определяется не только числом гармоник, но и энергетическим вкладом каждой из гармоник в общую энергию. Вопрос о качестве звукового тембра или о красоте звучания того или иного музыкального инструмента довольно субъективен, однако общие положения сводятся к тому, что звуковое колебание, бедное гармониками, представляется как звук глухой и бесцветный. Сочный звук воспринимается от звуков, в составе которых есть несколько первых гармоник с достаточно большими и не слишком отличающимися друг от друга энергиями. В том случае, когда в звуке преобладают высшие гармоники с большими относительными амплитудами, то это дает впечатление звука с резким, металлическим, а подчас пронзительным оттенком. Тембр звуков, создаваемых музыкальными инструментами, определяется не только различием в их конструкции, но и тем, как возбуждаются колеблющиеся детали инструмента. Так, например, выбор места удара фортепианного молоточка, прямо влияет на состав обертонов, окраску и полноту звука струны. Например, возбуждая струну точно на середине ее длины, мы выключаем из спектра звука все четные гармоники (на длине струны не укладывается четное число длин волн), а т.к. 2-я, 4-я, 6-я и т.д. гармоники как раз и являются самыми сильными и яркими, то звук, как говорят, получится "мертвым". Ударяя молоточком на 1/3 длины струны, выключим уже нечетные гармоники (на струне не укладывается нечетное число половинок длин волн), но состав спектра получается уже более богатым. Поэтому в практике форте-пианостроения уже давно установлено, что возбуждать струны молоточками целесообразно в басовом и теноровом регистрах на 1/8 их длины. В радиотехнике весь спектр сигнала тоже может быть разложен на гармоники начиная с первой (наименьшей).
Субъективизм слуха человека: границы частного диапазона звуков, тонкость слуха, динамические границы слышимости. Психофизический закон ВЕБЕРА-Фехнера. Децибельная шкала и ее построение. Уровни силы звука и уровни звукового давления. Кривые равной громкости. Сложение уровней силы звука. Диапазон звуковых частот, воспринимаемых молодым здоровым человеком, простирается от 16 до 20000 Гц, но участок наибольшей чувствительности ограничивается интервалом от 2000 до5500 Гц. Именно в данной области лежат резонансные частоты слухового прохода, причем усиливающих звук на 5-10 дБ. Ограниченность частотного диапазона, границы которого изменяются: с возрастом верхняя граница падает до 12000 Гц на высоких частота и заметно ослабляется на низких частотах. Другая особенность уха называется тонкостью слуха, т.е. способностью различить два звука порознь, а не как один звук. Увеличение частоты на 3 Гц становится заметным при частоте колебаний в 1000 Гц. Можно считать, что в пределах 600-4000 Гц относительное изменение частоты на 0,3 % становится впервые заметным. При более низких и более высоких звуках требуется большее изменение частоты для того, чтобы оно стало заметным. У музыкантов существуют два понятия, характеризующие способность ощущать высоту музыкальных звуков и оценивать их абсолютный и относительный слух. Абсолютным слухом называется сравнительно редко встречающаяся способность некоторых людей определять высоту заданного звука и называть ноту, которой этот звук соответствует, безотносительно к другим нотам, т.е. звука иной частоты. Человек, обладающий абсолютным слухом, может воспроизвести голосом любую заданную ему ноту, не сверяя ее ни с каким другим звуком. Относительным слухом обладает человек, способный определять и воспроизводить голосом заданные музыкальные интервалы, т.е. определять отношение между высотами звуков, оценивая их качественно как квиту, кварту, терцию и т.д. Очень важной особенностью слуха является то, что звуки разной высоты и одинаковой интенсивности воспринимаются по-разному. Человек субъективно их оценивает понятиями "громче", "сильнее", "слабее". В акустике же существует большое различие между двумя понятиями, которые в обычной жизни отождествляются (громкость и сила звука). Чтобы понять причины расхождения между физическими и физиологическими оценками одного и того же звука, необходимо рассмотреть две динамические границы слышимости, так называемые пороги слышимости. 1.Порогом болевого ощущения называется граница наиболее сильных звуков, восприятия которых сопровождается болезненным ощущением в ушах. Звуки такой большой силы вызывают, кроме боли в ушах, сравнимой с введением в слуховой проход твердого предмета, давящего на барабанную перепонку, целый ряд расстройств организма: головокружение, тошноту и другие недомогания. Для частоты 1000 Гц порог соответствует 100 Вт/м2, и звуковому давлению 200 Па, что соответствует тактильному чувству осязания. 2.Порогом слышимости называют границу еле слышимых звуков, столь незначительных по своей силе, что они практически не воспринимаются ухом. Для той же частоты 1000 Гц сила звука равна 10-12 Вт/м2, и звуковое давление 2-10 Па. Отметим, что эти границы соответствуют здоровому человеку в возрасте 20-25 лет. Таким образом, в отношении восприятия звуков столь различных по своей величине - больший звук в 10й раз выше минимального -практически трудно найти технический измерительный прибор с таким огромным диапазоном нагрузок при сохранении чувствительности при минимальных нагрузках. Это явление объясняется физиологическим законом Вебера-Фехнера: если величина раздражения, производимого внешней средой на человеческий организм, возрастает в геометрической прогрессии, то ощущения, испытываемые организмом, возрастают в арифметической прогрессии. Трансформируя этот закон в математическую форму можно сказать, что величина ощущения пропорциональна десятичному логарифму от величины раздражения. Закон Вебера-Фехнера только приблизительно описывает соотношение между величинами раздражения и ощущения, но удовлетворительно объясняет, каким образом наше сознание, вернее, наша нервная система, защищается от невероятного по своему диапазону скачка нагрузок - внешних раздражений, испытываемых ухом. Отметим, что этот закон распространяется не только на слуховое раздражение, но и на наш зрительный аппарат - глаз человека. Таким образом, минимальное значение энергии или звукового давления соответствует "нулевому" ощущению. В соответствии с этим законом была предложена следующая шкала(Децибельная шкала) соответствий ощущений и раздражений: раздражения - шкала значений интенсивности звука:10-12, 10-11,10-10,10-9,….,100 Вт/м2. ощущения - шкала значений громкости: 0, 1, 2, 3, 140. Между этими двумя шкалами следующая формула: LI = lg * (I/IO), где LI – громкость звука – уровень силы звука, IO = 10-12 Вт/м2. Единицу измерения громкости назвали бэлл. Ввиду того, что наше ухо может отличать звуки различающиеся на десятые доли бэлла, то бэлл разбили на 10 долей и назвали единицу громкости децибел (дБ). Если вместо интенсивности звуков использовать ее связь со звуковым давлением, то получим формулу (11): L = 10 lg*(p2ρ0c0/ρcp02) = 20 lg (p/p0) + 10lg ρ0c0/ρc, где p0c0 - акустическое сопротивление воздуха; pc- акустическое сопротивление той среды, где измеряется звуковое давление. Если все звуковые процессы происходят в воздушной среде при постоянной температуре и давлении, то второе слагаемое равно нулю и тогда громкость звука, выраженная через звуковое давление, называется уровнем звукового давления (для краткости обозначаемый у.з.д.), вычисляется по формуле: Lp=20lg(p/p0)(дБ). Таким образом можно говорить не только об энергетическом диапазоне сил звуков, воспринимаемых человеком, но и о диапазоне громкостей звуков (уровней звукового давления), который составляет 0-140 дБ. Наконец, существует еще одна очень важная особенность человеческого уха - его неодинаковая чувствительность к звукам различной частоты. На приведенной диаграмме (рис. 6) представлены кривые зависимости громкости от частоты, построенные на основании следующих экспериментов: исследуемый субъект обращается к источнику звуков, создающему чистые тона разной интенсивности, при этом источник и реципиент находятся в свободном звуковом поле и при этом сам исследуемый должен иметь здоровый слуховой аппарат и находиться в "нормальном" физическом и психологическом состоянии; кроме того он не должен видеть то, что делает экспериментатор. Сначала проверялось, на какой частоте порог слышимости равен минимальному значению интенсивности звука; это оказалась частота, лежащая в диапазоне 3000-4000 Гц. Порог слышимости для всех остальных частот оказался больше и составляет, например, для частоты 20 Гц примерно 70 дБ, а для частоты 10000 Гц около 20 дБ. Затем создавался эталонный сигнал на пороговой частоте с у.з.д., равным 10 дБ и с его громкостью сравнивался сигнал другой частоты, уровень которого подбирался таким, чтобы он казался равногромким с эталонным. На основании этого получили вторую кривую равной громкости; затем эталонный сигнал увеличивался еще на 10 дБ и снова производили эксперименты. В результате были получены кривые равной громкости диаграммы, которая представляет следствие закона Вебера-Фехнера: изменение чувствительности при изменении возбуждения обратно пропорционально значению абсолютного возбуждения, имевшей место до начала абсолютного возбуждения. Кроме указанных уже особенностей восприятия звуков органом слуха, нужно упомянуть об особом свойстве уха, называемом маскирующим эффектом, сущность которого состоит в том, что звук более сильный, заглушает (маскирует) звук более слабый. Последняя особенность - так называемый "бинауральный эффект", сущность которого сводится к тому, что благодаря наличию двух ушей человек определяет направление, по которому расположен источник звука. Для понимания его сущности достаточно сравнить восприятие звучания симфонического оркестра в зале и при воспроизведении монофонической записи: в зале с закрытыми глазами можем определить местонахождение инструмента в оркестре, а при слушании записи отсутствует ощущение распределения источников звука, которое появляется при стереофонической записи. Учитывая, что громкость связана с силой звука логарифмически, то суммарный уровень звукового давления при работе нескольких источников звука определяется по формуле: L = 10lg(100,1L1+100,1L2+….+100,1Ln). При одинаковых источниках звука общий уровень: L = 10lg n 100,1L1= L0 + 10lg n. Таким образом, если имеются два одинаковых по звуковой мощности источника звука, то общий уровень звука в помещении станет на 3 дБ больше, чем от одного.
Слоистые ЗПК(с использованием волокнист ЗПМ). Частотная характеристика слоистых звукопоглощающих конструкций. Влияние толщины слоя ЗПМ и плотности ЗПМ. Размещение пористого материала на относе от стенки, достоинства этого приема. Достоинства и недостатки ЗПМ,ЗПК. Звукоизоляция шума однослойными ограждениями. Зависимость звукоизоляции воздушного шума однослойными ограждениями от частоты и массы, размеров, упругости панелей, эффекта волнового совпадения. Возможные приемы исправления недостатков. Наиболее простые соотношения для звукоизоляции от воздушного шума были получены при рассмотрении нормального падения звука, когда любой слой ограждения ведет себя как твердая пластина, так как поперечные волны возникают только при косом падении звука. Если акустическое сопротивление среды, в которой распространяется вначале волна ρ1с1, а ограждения ρ2с2, толщина пластины δ и выполняется условие δ R0 = 10lg [ 1+ Из данной формулы видно, что звукоизолирующая способность воздушного шума в значительной степени определяется соотношениями между акустическими сопротивлениями сред. В частности, пористые материалы в "чистом" виде использовать не имеет никакого смысла, ибо их акустическое сопротивление не столь уж сильно отличается от акустического сопротивления воздуха и, чтобы получить заметную звукоизоляцию, надо взять очень толстый слой материала (сопоставимый с длиной звуковой волны), что для низких частот составляет несколько метров. Из приведенной выше формулы вытекают два случая, использующиеся на практике. Первый из этих случаев проявляется тогда, когда акустическое сопротивление преграды во много раз больше, чем воздуха (р2с2» р0с0). Это выполняется для обычно использующихся материалов при возведении ограждений зданий. При выполнении этого условия уравнение (27) упрощается: R0=10lg[1+(πm.ƒ/ где тn — поверхностная масса, кг/м2 (тn = 𝛾*δ,𝛾- плотность материала, кг/м3). Таким образом, видно, что звукоизолирующая способность растет с увеличением частоты звука и поверхностной массы ограждения. Вторая закономерность будет иметь место тогда, когда средой, окружающей ограждение, является не воздух. Если акустическое сопротивление этой среды много больше, чем "преграды" (
R0 = 10lg [ 1+((πδƒ/ Резюмируя, можно сказать, что R0 растет при уменьшении поверхностной жесткости преграды и это широко используется для звукоизоляции от структурных шумов посредством применения упругих прокладок (например, для губчатой резины р2с2 = 1,6*104 кг/(м2с) и, если ее поместить между двумя стальными элементами (переборками корабля), то получим эффект звукоизоляции (виброизоляции). Для помещений различного назначения звуковые волны падают на ограждение под всевозможными углами и, если размеры помещения достаточно велики по сравнению с длинами звуковых волн, то звуковое поле можно считать близким к диффузному. Тогда для определения эффекта звукоизоляции количественно, необходимо в уравнение коэффициента звукопроницания ввести его зависимость от угла падения. Найдя τ можно затем по формуле (25) вычислить R. В конечном счете, получаем формулу R = R0 – 10lg 0,23 R0, где RQ - звукоизолирующая способность при нормальном падении, определенная по формуле (28). Как показали измерения, в среднем величина Л на 5 дБ меньше Rq. В этом случае формула (30) преобразуется в более простую:
R = 20lg mnƒ – 47,5 Полученная зависимость отражает так называемый "закон массы": увеличение массы или частоты в два раза приводит к росту величины звукоизоляции на 6 дБ. Однако приведенные выше теоретические положения не полностью реализуются на практике, ибо возникает много обстоятельств, в результате которых поведение панели не следует "закону массы". Во-первых, на очень низких частотах передача звука через панель определяется ее упругими свойствами - при медленно меняющемся звуковом давлении панель будет выгибаться при положительном давлении и прогибаться назад при отрицательном (во вторую половину периода). Начиная с некоторой частоты падающей звуковой волны, панель начинает излучать большее значение энергии, чем можно было бы ожидать. Объясняется это тем, что частота внешнего периодического сигнала совпадает с первой основной частотой собственных колебаний панели (явление резонанса) - звукоизоляционный эффект снижается. Частоты этих резонансных колебаний незакрепленной панели определяются по формуле: ƒk,n=0,45*cпδ[(k/α)2+(n/b)2], (32) где cп — скорость распространения продольной звуковой волны в безграничной среде (панели); аиbлинейные размеры сторон панели; кип- целые числа, которые определяют количество полуволн, по которым изгибается пластина по двум взаимно-перпендикулярным направлениям. Для закрепленной панели (при k = п = 1) ƒ1,1= δ∆cп/α2, (33) ∆ = 5,14[1+(а/b)4] + 3,115* [а/b]2 (34) К счастью оказывается, что большинство ограждающих элементов в помещении крупноразмерны и найденные частоты панелей лежат близко к нижнему частотному пределу слышимости и из-за этого слабо воспринимаются ухом человека. Во-вторых, при наклонном падении звуковых волн на преграду может иметь место появление изгибных волн, как это изображено на рис. 18. Эти волны совсем иного типа, чем звуковые волны в твердой среде, но и они характеризуются некоторой частотой и длиной волны. При наклонном падении может оказаться, что длина звуковой волны в воздухе (λ0) и длина изгибной волны на панели (λu) совпадут. Это может быть отражено в формуле:
λu = λ0/sinƟ
Данное явление в литературе называется по-разному: коисциденс, резонанс совпадения, волновое совпадение. Последнее определение кажется более понятным, так как уравнение (35) связывает два вида волн. Наименьшая частота, при которой становится возможным волновое совпадение, получается при падении звуковой волны вдоль панели (Ɵ - 90°), т.е. в этом случае λu = λ0. Такую наименьшую частоту называют граничной и она может быть вычислена по формуле: ƒгр=0,55*со2/δ*сп, (36) где сп - скорость продольной волны в материале панели. Для звуковых волн, имеющих частоту большую, чем граничная, прохождение звука через панель при его диффузном падении определяется явлением волнового совпадения, так как из формулы (34) видно, что каждой частоте выше критической соответствует свой угол падения и панель имеет наибольшую звукопроницаемость. Приведенные выше соображения могут быть отражены на графике зависимости звукоизолирующей способности от частоты для четырех частотных диапазонов (рис. 19); в первом диапазоне звукоизоляция определяется жесткостью панели, во втором - резонансными явлениями на ней, третий диапазон начинается с двух-, трехкратной величины низшей (основной) резонансной частоты панели и подчиняется закону массы. Четвертый диапазон начинается с граничной частоты эффекта волнового совпадения и эффект звукоизоляции уменьшается. Провал характеристики в этой области тем больше, чем меньше затухание (непрерывная кривая на рисунке) и тем меньше, чем больше демпфирование панели (пунктирная кривая).
Для однослойных панелей, перегородок, у которых ƒгр > 1000 Гц рекомендуется уменьшать жесткость (увеличивать упругость) панели. Это не только уменьшает собственные резонансные частоты, но и укорачивает изгибную волну, которая снижает звукоизолирующие свойства панели, т.е. повышается граничная частота. В случае толстых панелей (l г р < 300 Гц) следует, наоборот, понижать критическую частоту путем увеличения жесткости панели за счет создания ребер жесткости или увеличением массы. Увеличение массы конструкции выгодно не только в силу закона массы, но и потому, что, не увеличивая упругость, удается снизить резонансные частоты. Наконец, если покрыть резонирующую перегородку слоем какого-либо пластичного материала, то при каждой деформации перегородки этот слой будет деформироваться и поглощать звуковую энергию. Однако это эффективно только для тонкослойных конструкций из фанеры, стали, алюминия и т.д. Итак, основные положения при проектировании однослойных ограждений сводятся к следующему: для всех частот, кроме самых низких, необходимо увеличивать массу панели на единицу ее площади, уменьшать упругость для толстых панелей и увеличивать ее для тонких, создавать условия для применения демпфирующих материалов с высоким затуханием. Размеры пластины - толщина, ширина и длина влияют на звукоизоляцию в разной степени. Толщина пластины входит в выражение поверхностной массы и цилиндрической жесткости. При увеличении толщины пластины больших размеров, если рассматривать отдельно области частот до и после критической, ее звукоизоляция всегда растет. Однако с увеличением толщины уменьшается граничная частота и, соответственно, докритические и за критические области частот передвигаются по частотной оси. В связи с этим тонкие пластины могут иметь в определенной области частот гораздо большую звукоизоляцию, чем относительно толстые. На первый взгляд звукоизоляция панели не должна зависеть от ширины и длины панели, исключая, конечно, резонансную область, так как в приведенные выше формулы (28) и (29) они не входят. Однако такое утверждение справедливо лишь для бесконечных по размерам пластин. Обычно понятие "звукоизоляция пластины" относится к единице площади, и в этом смысле звукоизоляция не зависит от общей площади пластины, а, следовательно, от размеров. Для реальных, ограниченных по площади панелей, зависимость звукоизоляции от общей площади проявляется в большей или меньшей степени. Проведенные эксперименты показывают, что звукоизоляция пластины будет мало зависеть от ширины и длины, если в минимальной из указанных размеров пластины укладывается больше четырех-пяти длин изгибных волн при ее жесткой заделке по контуру и более трех-четырех длин изгибных волн для свободно опертой пластины. На звукоизоляцию оказывает влияние и способ закрепления пластины по контуру. Установка звукоизолирующей конструкции на мягкие прокладки с повышенными потерями звуковой энергии способствует заметному увеличению звукоизоляции тонкой большой пластины, что может быть объяснено частичным заглушением свободных изгибных волн, отражаемых от краев. Поэтому контуры звукоизолирующих пластин желательно обрезинивать или заделывать мягкой пластмассой типа эластичного пенополиуретана, что опять же возможно только для тонкослойных конструкций.
27. Многослойные звукоизолирующие конструкции (типы). Некоторые особенности их применения. Факторы, обеспечивающие прирост звукоизоляции многослойных конструкций. Звукоизоляция многослойных ограждений Чтобы повысить звукоизоляцию кирпичной (бетонной) стены хотя бы на 6 дБ (что не очень значительно) необходимо увеличить толщину кладки в два раза. Понятно, что данный путь тупиковый, поэтому для увеличения звукоизоляции ограждающих конструкций используются многослойные конструкции, позволяющие увеличивать звукоизоляцию без существенного увеличения массы, что является весьма существенным в зданиях повышенной этажности. Многослойные ограждения можно условно разделить на две группы. К первой принадлежат конструкции из нескольких слоев жестко связанных друг с другом. Расчет их ничем не отличается от расчета однослойных ограждений. К другой группе относятся многослойные ограждения с упругими связями между составляющими жесткими слоями. В начале этой главы упоминалось о том влиянии, которое имеет волновое сопротивление при передаче звука. Если вместо удвоения массы раздвинуть перегородки, оставив между ними воздушный промежуток суммарная масса будет при этом вдвое больше, однако при этом появляются еще два фактора, влияющие на распространение звука, - дополнительные переходы звука из воздуха во вторую перегородку и из нее в воздух. Если бы такой воздушный промежуток был очень большой, то общий звукоизолирующий эффект равнялся бы арифметической сумме изоляций, создаваемых каждой из перегородок в отдельности. К сожалению, по строительным и прочим соображениям нельзя использовать очень большие воздушные промежутки и к тому же приходится их механически соединять, вследствие чего звукоизоляция оказывается много меньше максимально возможной. Если панели разные, то у каждой из них будет своя собственная частота эффекта волнового совпадения. Теория, разработанная В.И. Заборовым, показывает, что в области частот ƒ где d - толщина воздушного промежутка, м; тх и т2 - поверхностные массы панелей, кг/м2. Вследствие того, что на этой частоте наблюдается наибольшее прохождение звука, рекомендуется двойные ограждения проектировать так, чтобы эта частота лежала ниже наименьшей частоты нормируемого частотного диапазона. Для двойных ограждений с воздушным промежутком, у которых одна из пластин более легкая, т.е. m Двустенная конструкция с воздушным слоем на низких частотах вплоть до частоты, определяемой по формулам (37) или (38) не имеет никаких преимуществ перед одностенной конструкцией равной массы с точки зрения звукоизоляции и равна звукоизоляции однослойной конструкции с суммарной массой двух элементов. Кроме того, возможно даже некоторое понижение звукоизоляции вследствие резонанса конструкции, представляющих собой систему двух масс, соединенных упругой воздушной связью или мягким звукопоглощающим материалом. Специфические свойства увеличения звукоизоляции двустенной конструкции проявляются на средних и высоких частотах. Общий звукоизолирующий эффект в диапазоне частот
R = R0 + ∆R0, (39) где R0 - звукоизоляция однослойного ограждения с поверхностной массой m1 +т2 находится по закону массы; ∆ R0 - дополнительная звукоизоляция, определяется следующим образом: R0 = 40l g ( Так как fp имеет наименьшее значение при т] = т2, то разделенное двухслойное ограждение из двух одинаковых панелей обладает наибольшей звукоизолирующей способностью среди других двойных ограждений (при т1+т2= const и d = const). У двухслойного ограждения для одной и той же частоты существуют два угла для эффекта волнового совпадения. Для частот ƒ
где α- звукоизоляция воздушного шума плитой, имеющей большую цилиндрическую жесткость (условно D2 > D1), а ∆R = 40 lg ƒ /ƒp- + 20 lg (1 - αβ), (42) где a = m1/m2-; p = D2/D1; D - цилиндрическая жесткость для сплошной плиты, определяется из формулы: D = E*δ3/12(1-μ2), где μ - коэффициент Пуассона; Е – модуль Юнга. Анализ уравнения показывает, что на частотах выше граничных, звукоизоляция при прочих равных условиях выше для плит различной толщины. Оптимальным является отношение толщин, равное 2-4. Однако наибольший эффект звукоизоляции обнаруживается для двойных ограждений из плит одинаковой поверхностной плотностью, но различной цилиндрической жесткостью отличающейся в 6-7 раз. Казалось бы, что в принципе для двойных ограждений можно получить очень высокую звукоизоляцию (до 70-80 дБ). Однако за счет косвенных путей распространения звука в многоэтажных зданиях бывает трудно получить среднюю звукоизоляцию, превышающую 50-60 дБ. Если рассчитать дополнительную звукоизоляцию при установке второй плиты без жесткой связи по контуру, то ее звукоизоляция увеличивается от 10 дБ на низких частотах до более чем 30 дБ на высоких. Наличие же жесткой связи по контуру между панелями существенно изменяет прирост: при абсолютно жесткой связи Aft понижается до 6 дБ, а в реальных конструкциях соединений плит на средних и высоких частотах ∆R = 8-15 дБ, т.е. примерно в два раза меньше, чем при отсутствии связи по контуру. Введение мягких прокладок по периметру (резина типа 3311, 1847 и др.) дает величину∆R = 24—25 дБ. Существенное действие на прирост звукоизоляции оказывает введение между панелями звукопоглощающего материала. Исследования показали, что при этом его акустическое сопротивление должно быть близко к акустическому сопротивлению воздуха, а произведение его толщины на коэффициент затухания значительно больше единицы. Однако при этом толщина слоя ЗПМ должна быть не менее 50-100 мм, причем для достижения максимального эффекта увеличения звукоизоляции достаточно заполнить звукопоглощающим материалом только 2/3 воздушного промежутка. Реальное увеличение звукоизоляции составляет до 15 дБ на высоких частотах за счет того, что ЗПМ ликвидирует провалы минимумов звукоизоляции вблизи резонансных частот воздушного слоя. Следует упомянуть о трудностях, которые возникают при требовании увеличения звукоизоляции уже эксплуатируемых помещений. Обычно для этих целей используют многослойные конструкции. Однако известные способы их крепления к стене существенно снижают звукоизоляцию. Как правило, к стене через деревянную обрешетку или металлический профиль жестко на шурупах или гвоздях крепятся гипсокартонные или гипсово-локнистые листы или листы ДСПЛ Пространство заполняется утеплителем. Таким образом, звуковые вибрации передаются от стены через жесткие связи крепления и профиль на листы обшивки, которые и переизлучают их в изолируемое помещение. Поэтому вместо ожидаемого увеличения звукоизоляции на 10-15 дБ получаем 3-5 дБ, а иногда и менее. Этот недостаток был снижен в выпускаемой в настоящее время панели дополнительной звукоизоляции ЗИПС (1500x500 мм) толщиной от 40 до 130 мм. Основная панель ЗИПС (рис. 20) состоит из комбинации слоев: 1, 5 - пазогребневой гипсоволокнистый лист толщиной 20 мм; 2, 4 - слой супертонкого стекловолокна, 20 мм; 3 - лист гипсоволокнистый, 10 мм. Толщина звукоизолирующей панели и количество слоев может меняться в зависимости от конкретной задачи (от 40 до 130 мм и от трех до шести слоев). Принципиально новым в данной конструкции стал способ крепления панели к стене через виброразвязанные узлы на стадии производства. Проведенные измерения показали, что панель ЗИПС-7 толщиной 70 мм и поверхностной массой 40 кг/м2 создает дополнительную звукоизоляцию 7-9 дБ. ЗИПС-СУПЕР (толщина 130 мм за счет увеличения толщины слоев звукопоглощающего материала) имеет индекс дополнительной изоляции воздушного шума 13 дБ.
Эти панели просты в монтаже, крепятся гвоздями или шурупами, подлежат монтажу и демонтажу без ухудшения акустических и эксплуатационных свойств. Сложность применения данной конструкции заключается в том, что в заселенных зданиях недостаточно увеличить звукоизоляцию стены от шумного соседа, так как не малая часть излучения будет идти от поверхностей других ограждающих конструкций. Поэтому приходится решать задачу комплексно, увеличивая звукоизоляцию и других ограждающих конструкций. Необходимо отметить еще одно обстоятельство при использовании дв
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.87 (0.016 с.) |

 f H f В. Полоса частот, у которой отношение f %0 / f = 2, f р = 1,41 f, называется октавой. Если f %0 / f =
f H f В. Полоса частот, у которой отношение f %0 / f = 2, f р = 1,41 f, называется октавой. Если f %0 / f =  , f р = 1,12 f, то ширина полосы равна третьоктавы. Набор октавных полос, использующихся для анализа шума, стандартизован и начинается с частоты 31,5 Гц: 31,5; 63; 125; 250,..., 8000 Гц. Каждая октавная полоса состоит из трех третьоктавных полос; скажем, октавная полоса 125 Гц из третьоктав 100, 125, 160 Гц.
, f р = 1,12 f, то ширина полосы равна третьоктавы. Набор октавных полос, использующихся для анализа шума, стандартизован и начинается с частоты 31,5 Гц: 31,5; 63; 125; 250,..., 8000 Гц. Каждая октавная полоса состоит из трех третьоктавных полос; скажем, октавная полоса 125 Гц из третьоктав 100, 125, 160 Гц. , где λ – длины падающей звуковой волны, то звукоизолирующая способность однослойного ограждения от воздушного шума оценивается выражением:
, где λ – длины падающей звуковой волны, то звукоизолирующая способность однослойного ограждения от воздушного шума оценивается выражением: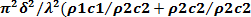 )2] (27)
)2] (27) )2] (28)
)2] (28)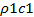 »
»  ), то в этом случае формула (4) преобразуется в выражение:
), то в этом случае формула (4) преобразуется в выражение: )2], (29) где kp — модуль объемной упругости материала второй среды.
)2], (29) где kp — модуль объемной упругости материала второй среды.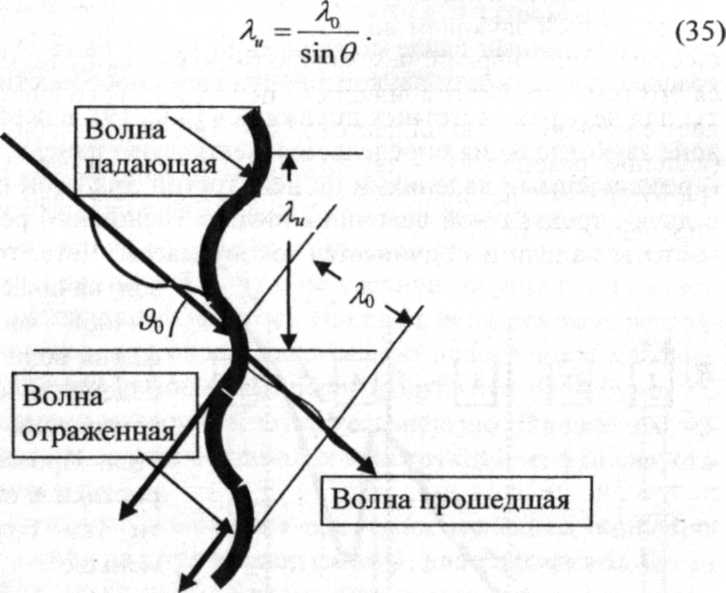

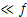 гр1 и ƒ
гр1 и ƒ  1/d(1/m1+1/m2) (37)
1/d(1/m1+1/m2) (37) то резонансная частота при тех же единицах измерения равна ƒp=85/
то резонансная частота при тех же единицах измерения равна ƒp=85/ 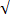 dm2
dm2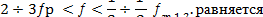
 / ƒp) (40)
/ ƒp) (40) значение звукоизоляции двойного ограждения имеет вид:
значение звукоизоляции двойного ограждения имеет вид: R=R2 + ∆R (41)
R=R2 + ∆R (41)



