
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение усилий в главных балках пролетных строений и определение требуемых размеров их поперечных сечений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1) метод рычага Наибольшее давление продольных рядов подвижной нагрузки на каждую из главных балок (ферм) находят умножением этой нагрузки на η=КПУ (коэффициент поперечной установки), зависящий от размещения нагрузки относительно главных балок и различный для каждой из них. Определяются моменты и поперечные усилия при 2 случаях загружения. 1) в крайней балке: Мl/2=η1∙(Рl/4); η1=1,0; η2=0; Мl/2=0. 2) во второй балке: η1=0; η2=1,0; Мl/2=1∙(Рl/4). 3) η=0,5. Тележка 1) в крайней балке: Мl/2=η1∙(Рl/4); η1=1/2(у1+у2); М1=1/2(у1+у2) ∙Р∙∑уі; 2) во второй балке: Мl/2=1/2(у1+у2+у3+у4) ∙(Рl/4); η2=1/2(у1+у2+у3+у4). метод внецентренного сжатия При его использовании предполагается, что балки и плиты пролетного строения тесно связаны между собой и поперечная жесткость велика. При произвольномнагружении поперечное сечение пролетного строения не деформируется, а лишь опускается и поворачивается на некоторый угол за счет упругости главных балок. Строим линии влияния давлений на отдельные главные балки. Линии влияния опорных давлений имеют прямолинейное очертание и для построения каждой из них необходимо найти две ординаты при положении груза Р=1 под крайними балками. Р=1 заменяется действием груза Р1 (над крайними балками Р=1) приложенного по оси моста и моментом М=Р∙е. ↓ линия влияния опорного давления Если поперечное сечение всех балок не одинаково груз Р=1 и М=1ьбудут распределены между балками прапорционально их жесткостям, в таком случае величины ординат линий влияния на крайний левый прогон (правый) определяют по ф-ле:
Где Если все балки пролетного строения имеют одинаковое поперечное сечение
Для расчета давлений для 1-й балки:
Разрезная система: Линию влияния опорных давлений загружают как обычно наиболее невыгодным способом (первый случай АК и второй) и находят КПУ как и в способе рычага. Этот способ хорош в середине пролета.
Проверка прочности сечений стальных балок.
Прочность стальных сечений, работающих на изгиб, проверяют по нормальным, касательным и приведенным напряжениям. Проверку по нормальным напряжениям выполняют с учетом ограниченного развития пластических деформаций в сечении:
где М — наибольший расчетный изгибающий момент в сечении; Wn — момент сопротивления сечения с учетом ослаблений сечения; x— коэффициент, учитывающий ограниченные пластические деформации в сечении; Ry — расчетное сопротивление металла балки; т — коэффициент условий работы, Коэффициент x зависит от касательных напряжений в сечении: если средние касательные напряжения в стенке балки x = xi, где xi — коэффициент, зависящий от отношений площади сечения меньшего пояса балки к площади сечения стенки. Если х = 1,155 xi где Q — расчетное значение поперечной силы в сечении; Q u—предельная поперечная сила; Qu = Rs тх2It/S, I —момент инерции сечения учета ослаблений; t — толщина стенки; S—статический момент части сечения до центра тяжести сечения; x 2= 1,25 - 0,25 Минимальные и максимальные касательные напряжения в сечении стенки:
где — S max-min соответственно статические моменты части сечения до уровня центра тяжести сечеиия и до уровня, соответствующего наименьшим касательным напряжениям в стенке (в месте примыкания к поясу)
Проверку стенки по кас. напряжениям выполняют с учетом пласт деформаций
Эти формулы действительны для любых сечений: двутавровых, коробчатых, тавровых. Кроме проверок прочности по нормальным и касательным напряжениям, стенки балок должны удовлетворять условия
Проверки прочности стальных сечений, работающих на изгиб, обычно дают возможность определить их размеры. Как и все инженерные расчеты, эти проверки выполняют с точностью ±5%. Необходимо отметить, что сортамент прокатного металла влияет на точность выполнения расчетов.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 769; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 .
. - момент инерции крайней левой балки;
- момент инерции крайней левой балки;  - моент инерции; аi – расстояние между симметричными осями i- тых симметричных прогонов.
- моент инерции; аi – расстояние между симметричными осями i- тых симметричных прогонов. =
= 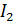 =
=  =… - ф-ла имеет вид:
=… - ф-ла имеет вид: .
.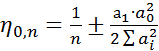 .
. х = M/хWn<Rym,
х = M/хWn<Rym, т не превышают четверти расчетного сопротивления на сдвиг металла стенки Rs (
т не превышают четверти расчетного сопротивления на сдвиг металла стенки Rs ( ,
, max
max max-min= QS max-min /It
max-min= QS max-min /It = QS/x2It≤ Rsт,
= QS/x2It≤ Rsт, ≤
≤ 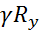 m
m


