Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні характеристики потоку руху рідини .Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Розрізняють два основних види руху рідини усталений і неусталений. При усталеному або постійному в часі називають такий рух рідини при якому всі параметри які характеризують параметри тіла в даній точці простору з часос незмінюються, а змінюються лише при переході до іншої точки простору при доному виді руху; Неусталеним рухом називається такий рух при якому швидкість і гідродинамічний тиск в кожній точці постійно змінюється тобто залежить не тільки від координати точки а і від часу
Основні критерії подібності при русі в”язких і в”язкопластичних рідин. Критерії подібності руху рідини визначаються відношенням відповідних сил, складених для характерного лінійного розміру d рідини. Нижче наводяться основні критерії подібності при русі в’язких і в’язкопластичних рідин: 1. 2. 3. 4. 5. 6. 7. Для круглих труб в якосты характерного лыныйного розмыру приймається їх внутрішній діаметир (d), а для кільцевих труб різниця діаметрів (D-d). Перехід ламінарного руху в турбулентний оцінюють критичними значеннями середньої швидкості руху або чисел Рейнольдса, знайденими експериментально. Для вязкої рідини
або наближену формулу, яка придатна для інженерних розрахунків при Типи рідин (основні реологічні моделі).
Реолопя — це наука про текучусть і деформацю суцільних середовищ. Реолопчні рівняння визначають в загальному випадку залежність між тензорами напружень і деформацій або похідними цих тензорів у часі. Склалярні коефціенти таких залежностей характеризують реологічні властивості середовища. У найпростшому випадку реологічні моделі (рівняння) визначають залежнють між дотнчними напруженнями зсуву 1. ідеальна 2. пружна (Гука) 3. в'язка (Ньютона) 4. жорсткопластична (Сен-Венана) 5. в'язкопластична (Шведова-Б1нгама 6. степенева (Оствальда) 7. нелінійна в'язкопластична (Гершеля-Балклі) 8. в'язкопружна (Максвела) 9. в'язкопружна (Кельвіна-Фойгта) До реолопчних властивостей належать скалярні величини: G — модуль пружності при зсуві;
k — міра консистенції; n — показник нелінійності. средовища, які підпорядковуються реологічній моделі Ньютона називають нютонівськими, а решта — неньютонівськими. До нютонівських рідин належить вода, розсоли, дегазоваж нафта і нанатпродукти, які немістять парафінів, асфальтенів, смол і багато інших однофазних рідин.
Гідравлічні втрати тиску в трубах при ламінарному русі в’язкої рідини.
Гідравлічні втрати тиску при ламінарному русі в'язкої рідини в трубах з постійним перерізом, як правило, вираховують за формулою Дарсі-Вейсбаха
де
де
де
Інтегрування рівняння (1) дає можливість отримати необхідні для виконання практичних розрахунків співвідношення між витратою іперепадом тиску при будь якому вигляді функції Проінтегруємо рівняння (1)
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

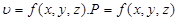 є координакти точки яка рухається і звідци виходить що через кожну визначену точку заповнену рідиною проходять частинки, а елементи її руху тотожні, а тому частинки переміщуються тієюж траекторією одна за одною. Прикладом є рух рідини при постійній витраті.
є координакти точки яка рухається і звідци виходить що через кожну визначену точку заповнену рідиною проходять частинки, а елементи її руху тотожні, а тому частинки переміщуються тієюж траекторією одна за одною. Прикладом є рух рідини при постійній витраті.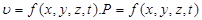 Прикладом є витікання рідини їз резервуара коли рівень води знижується
Прикладом є витікання рідини їз резервуара коли рівень води знижується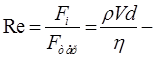 критерій Рейнольдса;
критерій Рейнольдса;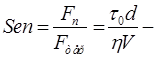 критерій Сен-Венана-Іллюшина;
критерій Сен-Венана-Іллюшина;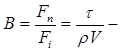 критерій пластичності;
критерій пластичності;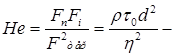 критерій Хедстрема;
критерій Хедстрема;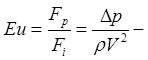 критерій Ейлера;
критерій Ейлера;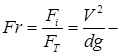 критерій Фруда;
критерій Фруда;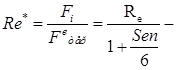 узагальнений критерій Рейнольдса;
узагальнений критерій Рейнольдса;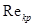 =2100-2300. Для вязкопластичної рідини застосовують формулу Соловйова
=2100-2300. Для вязкопластичної рідини застосовують формулу Соловйова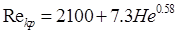 ,
,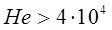 ,
, 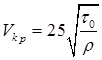
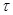 та деформацією зсуву
та деформацією зсуву 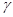 або її градієнтом
або її градієнтом 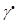 . Основні реологічні моделі середовищ:
. Основні реологічні моделі середовищ: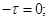
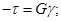
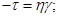
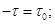
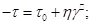
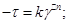
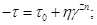
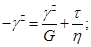
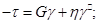
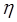 — в'язкість;
— в'язкість;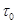 — динамічне напруження зсуву;
— динамічне напруження зсуву;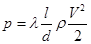
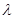 -- коефцієнт гідравлічного опору в трубах;
-- коефцієнт гідравлічного опору в трубах;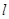 - довжина труби, м;
- довжина труби, м;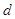 -- внутрішній діаметр трубм, м;
-- внутрішній діаметр трубм, м;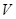 -- середньооб'емна швидюсть руху рідини, м/с;
-- середньооб'емна швидюсть руху рідини, м/с;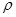 -- густина рідини, кг/м3.
-- густина рідини, кг/м3.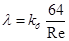
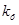 -- коефіцієнт що залежить від форми поперечного перерізу(для круглих труб =1)
-- коефіцієнт що залежить від форми поперечного перерізу(для круглих труб =1)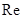 -- критерій рейнольдса.
-- критерій рейнольдса.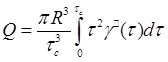 (1)
(1)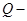 витрата БР,
витрата БР,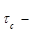 дотичне напруження зсуву на стінці труби.
дотичне напруження зсуву на стінці труби.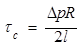
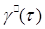 . Для вязкої рідини формула витрати при лам. Режимі може бути одержана якщо рівняння (1) замість
. Для вязкої рідини формула витрати при лам. Режимі може бути одержана якщо рівняння (1) замість 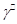 підставити її значення
підставити її значення 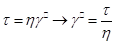
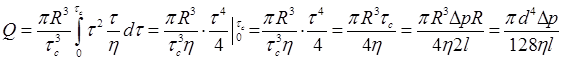
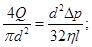
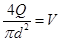 ;
; 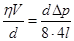 ;
; 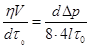 ;
; 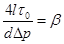 ;
; 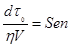 ;
;