
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійний поворотний трансформаторСодержание книги
Поиск на нашем сайте
На вторинному боці поворотного трансформатора виникає напруга, яка залежить від Cosα або Sinα. Якщо необхідно в якійсь схемі пристрою з поворотним трансформатором одержати лінійну залежність U2(α), то можливо скористатись обмеженою ділянкою U2s(α) для синусної обмотки. Межі цієї ділянки визначаються допустимою погрішністю, оскільки в цьому разі вважається α≈Sinα. Наприклад, якщо допустима погрішність 0.1%, то ділянка характеристики визначається ±4.5º. Ширший діапазон зміни α можливо одержати зі спеціальними схемами з’єднань обмоток поворотного трансформатора, які забезпечують
Функція:
при певних значеннях m буде майже лінійною в досить широкому діапазоні зміни Будемо вважати
Поділимо (17.47) на (17.48) за формулою (17.46):
а) б) Рис. 17.5. Схеми первинного (а) та вторинного (б) симетрування ЛПТ
Вважаємо, що αmах = ±0.3π ≈ ±1 рад. Підставляючи αmах у формулу (17.49), одержимо
тобто залежність практично лінійна в діапазоні кутів ±αmах. Точний аналіз ƒ (α) при різних значеннях т показує, що при т=0.54 αmах=±60º погрішність не перевищує 0.06%. Для одержання лінійної залежності (17.45) можуть бути використані дві схеми: з первинним або вторинним симетруванням. На рис.17.5, а подано схему з первинним, а на рис.17.5, б – зі вторинним симетруванням. При первинному симетруванні (рис.17.5, а) поперечна МРС
Для ланцюга навантаження
Вирішуючи сумісно (17.50), (17.51), одержимо:
тобто за формою (17.52) співпадає з (17.45) при
Оскільки Fq та Фq в схемі зкомпенсовані відповідно FК та ФК, зміна навантаження не впливає на лінійність вихідної характеристики. Вхідний опір залежить, а вихідний – не залежить, від кута повороту ротора. При вторинному симетруванні компенсаційна та синусна обмотки з’єднуються послідовно. В їхній контур вмикається опір навантаження zн (рис.17.5, б). Симетрування здійснюється вмиканням в ланцюг косинусної обмотки опору zнс. Величина цього опору підбирається таким чином, щоб
Як показує аналіз, для додержання умови (17.55) співвідношення між зведеними до первинного боку опорами ланцюгів синусної й косинусної обмоток повинні бути
де Якщо поперечний потік Фq повністю зкомпенсований, то в машині діє подовжній потік Фd, який створюється головною обмоткою С1-С2, та поперечний потік компенсаційної обмотки ФК. В цьому разі ЕРС синусної обмотки є сумою ЕРС Е2, наведеної потоком Фd, та Е2н, наведеної потоком взаємоіндукції ФК:
Але
де хт – опір намагнічуючого контуру Тоді з (17.57)÷(17.59):
Поява величини Оскільки
враховуючи (17.61) в (17.60), одержимо:
або, нехтуючи спадами напруги в обмотках:
Таким чином, залежність (17.62) за формою співпадає з (17.45) при А за формулою (17.53), а
Недоліком схеми з вторинним симетруванням є те, що вона не може бути використана в тих випадках коли zн=var. Лінійний поворотний трансформатор може працювати як в режимі повороту, так і безперервного обертання. В останньому випадку миттєве значення вторинної напруги без врахування ЕРС обертання дорівнює:
або
Як це випливає з (17.65), поворотний трансформатор створює пучки імпульсів, в яких початкова частина обвідної зростає лінійно приблизно до 60º.
Поворотний трансформатор–побудувач та Перетворювач координат
Рис. 17.6. Схема для вирішення прямокутного трикутника
За допомогою поворотних трансформаторів здійснюється перетворення координат на площині (від декартової системи до полярної; від однієї декартової системи до іншої, яка повернута на певний кут α, та низку інших перетворень), визначення гіпотенузи прямокутного трикутника та одного з гострих кутів за двома катетами.
Рис. 17.7. Заданий прямокутний трикутник Схема для вирішення прямокутного трикутника наведена на рис.17.6. На схемі наведено механічне з’єднання роторів поворотного трансформатора та виконавчого двигуна з амплітудно-фазовим керуванням через редуктор. Будемо вважати, що задано прямокутний трикутник, який має сторони з довжинами а, b, с (рис.17.7).
Відомі катети b і с. потрібно визначити гіпотенузу а й кут α. Довжини катетів задаємо за допомогою подільника R (рис.17.6) у вигляді напруг:
МРС головної та компенсаційної обмоток створюють пульсуючий магнітні потоки
Результуючий потік дорівнює:
Цей потік наводить в роторних обмотках ЕРС:
Припустимо, що в початковий момент часу (до вмикання
Нехтуючи спадом напруги в обмотці, можливо записати:
Таким чином, гіпотенуза а пропорційна напрузі
Рис. 17.8. Схема вмикання перетворювача координат
За допомогою поворотного трансформатора можливо перетворювати одну систему координат в іншу, повернуту на деякий кут α. Для цього суміщують вихідну систему координат з осями обмоток статора, а перетворену – з осями обмоток ротора (рис.17.8). При вмиканні обмоток С1-С2 та К1-К2 на синфазні напруги
Складові ЕРС у (17.74), (17.75) дорівнюють:
Підставляючи з (17.76)÷(17.79) у (17.74), (17.75) з урахуванням (17.68), (17.69) одержимо, вважаючи
Формули (17.80), (17.81) відповідні співвідношенням між координатами повернутих осей у декартовій системі. Якщо
то
Оскільки за схемою рис.17.6 визначається довжина гіпотенузи прямокутного трикутника й кут α за двома катетами, це відповідно переходу від декартової системи координат (катети) до полярної (гіпотенуза й кут). В цьому режимі, як і в попередніх, здійснюється симетрування: а) первинне при z1=zк; zs≠zc; б) вторинне при zs=zc; z1≠zк; в) первинне та вторинне при z1=zк; zs=zc; При первинному симетруванні перетворювача координат
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.009 с.) |

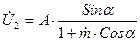 . (17.45)
. (17.45)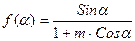 (17.46)
(17.46) .
.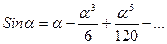 (17.47)
(17.47)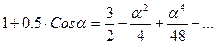 (17.48)
(17.48)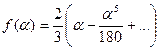 . (17.49)
. (17.49)
 ,
, компенсується МРС квадратурної обмотки
компенсується МРС квадратурної обмотки 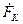 . Тому достатньо точно можливо вважати, що ЕРС в обмотках створюються тільки подовжнім магнітним потоком
. Тому достатньо точно можливо вважати, що ЕРС в обмотках створюються тільки подовжнім магнітним потоком  . Тоді для ланцюга збудження, нехтуючи спадами напруги в обмотках:
. Тоді для ланцюга збудження, нехтуючи спадами напруги в обмотках: . (17.50)
. (17.50) . (17.51)
. (17.51) , (17.52)
, (17.52) , (17.53)
, (17.53) . (17.54)
. (17.54) . (17.55)
. (17.55) , (17.56)
, (17.56)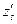 ,
,  ,
,  – відповідно зведені до первинного боку опори синусної, компенсаційної та косинусної обмоток.
– відповідно зведені до первинного боку опори синусної, компенсаційної та косинусної обмоток. . (17.57)
. (17.57) ; (17.58)
; (17.58) , (17.59)
, (17.59) . (17.60)
. (17.60) у другому доданку (17.60) є результатом зведення до первинного боку струму Іs та опору хт.
у другому доданку (17.60) є результатом зведення до первинного боку струму Іs та опору хт. , (17.61)
, (17.61) ,
, . (17.62)
. (17.62) . (17.63)
. (17.63) , (17.64)
, (17.64) . (17.65)
. (17.65)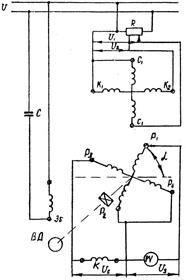

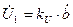 , (17.66)
, (17.66) . (17.67)
. (17.67)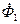 та
та  , осі яких нерухомі у просторі. Якщо машина не насичена, то модулі
, осі яких нерухомі у просторі. Якщо машина не насичена, то модулі  та
та  . Додаючись, потоки
. Додаючись, потоки  , вектор якого створює за осями головної й компенсаційної обмоток такі ж кути, як і гіпотенуза а з катетами b та с. Подовжня та поперечна складові результуючого потоку наближено дорівнюють:
, вектор якого створює за осями головної й компенсаційної обмоток такі ж кути, як і гіпотенуза а з катетами b та с. Подовжня та поперечна складові результуючого потоку наближено дорівнюють: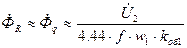 ; (17.68)
; (17.68)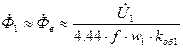 . (17.69)
. (17.69) . (17.70)
. (17.70) ; (17.71)
; (17.71)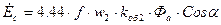 . (17.72)
. (17.72)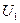 та
та  ) α=0, тобто осі обмоток Р3-Р4 та С1-С2 співпадають (рис.17.6). При подачі напруг
) α=0, тобто осі обмоток Р3-Р4 та С1-С2 співпадають (рис.17.6). При подачі напруг  наведе в обмотках ротора ЕРС у відповідності з (17.71), (17.72). Виконавчий двигун почне обертатись, і його обертання буде продовжуватись до того моменту часу, доки на затискачах обмотки керування «К» буде напруга, тобто до тих пір, доки обмотка Р3-Р4 не займе положення, при якому її вісь буде перпендикулярною до осі магнітного потоку
наведе в обмотках ротора ЕРС у відповідності з (17.71), (17.72). Виконавчий двигун почне обертатись, і його обертання буде продовжуватись до того моменту часу, доки на затискачах обмотки керування «К» буде напруга, тобто до тих пір, доки обмотка Р3-Р4 не займе положення, при якому її вісь буде перпендикулярною до осі магнітного потоку  ;
;  .
.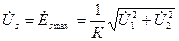 . (17.73)
. (17.73) при нерухомому роторі, а кут α дорівнює одному з гострих кутів прямокутного трикутника.
при нерухомому роторі, а кут α дорівнює одному з гострих кутів прямокутного трикутника.
 ; (17.74)
; (17.74) . (17.75)
. (17.75) ; (17.76)
; (17.76) . (17.77)
. (17.77)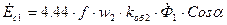 ; (17.78)
; (17.78)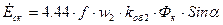 . (17.79)
. (17.79)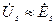 ;
;  :
: ; (17.80)
; (17.80) ; (17.81)
; (17.81) , (17.82)
, (17.82)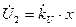 . (17.83)
. (17.83) , (17.84)
, (17.84) . (17.85)
. (17.85)


