
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переваги й недоліки синхронних реактивних двигунівСодержание книги
Поиск на нашем сайте
Можливість роботи синхронного двигуна звичайної конструкції при відсутності збудження була вперше виявлена Сіменсом у 1874 р., коли він випадково вимкнув збудження у синхронного двигуна, який продовжував після цього обертатись. Але в той час це явище не було пояснене й розглядалось як цікавий курйоз. Лише через 20 років Блондель запропонував метод аналізу на основі теорії двох реакцій, за допомогою якого й пояснили принцип дії синхронного реактивного двигуна. У зв'язку з тим, що основний магнітний потік у двигуні створюється МРС реакції якоря, він називається реактивним. Основною відмінністю синхронних реактивних двигунів є те, що вони не мають збудження з боку ротора. А звідси – простота конструкції, порівняно низька вартість та висока надійність, пов'язана з відсутністю швидко зношуваних частин (колектор, контактні кільця, щітки) та збуджувача. Недоліками цих двигунів, які обмежують області їх застосування, є споживання ними з мережі реактивної потужності, що зменшує максимальний момент
Обертаючий момент і електромагнітна потужність синхронних реактивних двигунів (СРД)
В машинах великої й середньої потужності, які розглядаються у загальному курсі електричних машин, для спрощення аналізу при визначенні електромагнітних моменту
Рис. 12.5. Векторна діаграма явнополюсного синхронного двигуна
Для визначення цих величин та уточнення принципу дії СРД розглянемо спочатку роботу звичайного явнополюсного синхронного двигуна в режимі недозбудження. Цьому випадку відповідна векторна діаграма рис.12.5.
Судячи з наведеної векторної діаграми, висновуємо, що при недозбудженні синхронний двигун споживає з мережі струм, який відстає від напруги за фазою та створює подовжню підмагнічуючу МРС Якщо довести струм збудження ротора (а отже й
Рис. 12.6. Векторна діаграма синхронного реактивного двигуна
Спочатку визначимо електромагнітну потужність:
Потужність споживання з мережі:
де Враховуючи те, що
одержимо:
Але:
З системи рівнянь (12.13) визначаються струми:
Підставимо з (12.14), (12.15), (12.12) у (12.7) та після перетворень одержимо: З урахуванням (12.16) підраховується електромагнітний момент:
Якщо у відповідності з виразами (12.17), (12.16) побудувати низку залежностей
Рис. 12.7. Кутові характеристики синхронного реактивного двигуна
З формул (12.16), (12.17) видно, що
З формули (12.19) видно, що зі зменшенням Синхронізуючий момент
тобто, якщо r=0 й θ=0, то
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.006 с.) |

 , cos φ (звичайно 0.5), ККД (при номінальній потужності
, cos φ (звичайно 0.5), ККД (при номінальній потужності 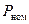 у кілька десятків ват η=30-40%, а при
у кілька десятків ват η=30-40%, а при  від часток до одиниць ват η=5-25%) та збільшує габарити й масу, велика чутливість до коливань напруги U мережі, оскільки електромагнітний момент прямо пропорційний
від часток до одиниць ват η=5-25%) та збільшує габарити й масу, велика чутливість до коливань напруги U мережі, оскільки електромагнітний момент прямо пропорційний  , та схильність до коливань ротора при раптових коливання моменту навантаження
, та схильність до коливань ротора при раптових коливання моменту навантаження  або кутової частоти обертання ω.
або кутової частоти обертання ω. й потужності
й потужності  наближено вважається активний опір обмотки статора дорівнюючим нулеві. Для цих машин таке припущення не створює великих погрішностей, оскільки
наближено вважається активний опір обмотки статора дорівнюючим нулеві. Для цих машин таке припущення не створює великих погрішностей, оскільки  та
та  . В мікромашинах активний опір r такого ж порядку, як
. В мікромашинах активний опір r такого ж порядку, як  й
й  , тому припущення
, тому припущення  створює великі погрішності. У зв’язку з цим необхідно при визначенні
створює великі погрішності. У зв’язку з цим необхідно при визначенні 
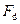 . Фізично це пояснюється тим, що при U=const результуючий магнітний потік
. Фізично це пояснюється тим, що при U=const результуючий магнітний потік  . Тому нестача або надлишок МРС збудження
. Тому нестача або надлишок МРС збудження  компенсується підмагнічуючою або розмагнічуючою
компенсується підмагнічуючою або розмагнічуючою 
 (12.7)
(12.7) , (12.8)
, (12.8) - фазна напруга.
- фазна напруга. (12.9)
(12.9) , (12.10)
, (12.10) , (12.11)
, (12.11) (12.12)
(12.12) . (12.13)
. (12.13) (12.14)
(12.14) (12.15)
(12.15)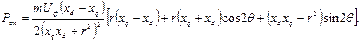 (12.16)
(12.16) (12.17)
(12.17) при фіксованих значеннях інших величин, то одержимо графіки рис.12.7, з яких видно, що зі збільшенням r зменшується
при фіксованих значеннях інших величин, то одержимо графіки рис.12.7, з яких видно, що зі збільшенням r зменшується 
 та
та  , тобто коли машина явнополюсна. Звідси виходить, що СРД повинен бути принципово явнополюсним. Щоб спростити подальший аналіз, вважаємо
, тобто коли машина явнополюсна. Звідси виходить, що СРД повинен бути принципово явнополюсним. Щоб спростити подальший аналіз, вважаємо  Тоді з формули (12.17), (12.16):
Тоді з формули (12.17), (12.16): (12.18)
(12.18) (12.19)
(12.19) збільшується
збільшується  , (12.20)
, (12.20) =0, а якщо
=0, а якщо  , то
, то



