
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Робота контактних сельсинів у індикаторному режиміСодержание книги
Поиск на нашем сайте
Як уже зазначалось, основними режимами роботи однофазних сельсинів є індикаторний та трансформаторний. Схеми багатократного прийому та з диференціальним сельсином також належить до індикаторного режиму. У тих випадках, коли необхідно передати на відстань кутове положення якогось пристрою, застосовується індикаторний режим (положення клапана, заслінки, стрижнів у ядерному реакторі і т. д.). В цьому режимі на валу сельсина-приймача виникає малий момент опору (навантаженням може бути, наприклад, стрілка приладу), тому малий обертаючий момент може бути одержаний від самого сельсина без допоміжних підсилюючих пристроїв.
Рис.16.5. Схема з’єднання сельсинів у індикаторному режимі
На рис.16.5 наведена схема з’єднання сельсинів у індикаторному режимі. Проходячи по обмотці збудження, однофазний струм створює пульсуючий магнітний потік, який наводить синфазні і різні за величиною ЕРС в кожному промені обмотки синхронізації. Якщо положення обмоток синхронізації відносно обмоток збудження однакові у датчику Д та приймачі П (θ=0), то ЕРС променів взаємно врівноважуються. Тому струм в їхньому ланцюзі відсутній. З появою кута непогодження (θ≠0) рівновага ЕРС порушується, в ланцюгах обмоток синхронізації виникають зрівняльні струми, які, взаємодіючи с пульсуючим потоком збудження, створюють синхронізуючий момент. Оскільки датчик, з’єднаний із задаючим механізмом, не може повертатися сам, синхронізуючий момент діє лише на приймач. В результаті цього приймач повертається до тих пір, доки момент не стане дорівнювати нулеві, тобто в ідеальному випадку, поки ЕРС в обмотках синхронізації знову не врівноважаться. Приймач відпрацьовує кут, заданий датчиком.. Наявність в однофазних сельсинах електричної (однофазна обмотка збудження) та магнітної (явно виражені полюси) асиметрії створює деякі особливості аналізу процесів у таких машинах. Робота сельсина-приймача в індикаторному режимі характеризується такими основними показниками: 1) залежністю Мс(θ); 2) значеннями Мсmax та 3) максимальними значеннями статичної та динамічної похибок в режимах повороту й обертання; 4) максимальною швидкістю обертання, при якій динамічна похибка знаходиться в допустимих межах;
5) часом погодження датчика та приймача після початкового непогодження на 180º. В результаті аналізу електромагнітних процесів у сельсинах визначимо вищенаведені залежності. В теорії сельсинів використовується теорія або синхронних, або асинхронних машин. Теорія синхронних машин (метод двох реакцій) краща при розгляді сельсина в режимі синхронного обертання. Для спрощення аналізу будемо виходити з таких припущень. 1. Реакцією якоря нехтуємо, що є допустимим при малих практично використовуваних кутах непогодження θ. 2. Магнітний ланцюг машини не насичений, тобто μ→∞, а просторовий розподіл МРС у повітряному зазорі синусоїдний. 3. Датчик та приймач є двополюсними машинами однакової конструкції. 4. Від датчика працює тільки один приймач. У загальному випадку ротори датчика й приймача можуть бути повернуті на різні кути θд й θп. Кут непогодження θ між ротором датчика та приймача дорівнює (рис.16.5):
Оскільки ЕРС відповідних променів датчика й приймача діють зустрічно, то, за наявності нульового дроту в обмотці синхронізації, між відповідними затискачами сельсинів діють ЕРС:
З формули (16.12):
Тоді з (16.15) з урахуванням (16.16):
Струми в лініях зв’язку можуть бути визначені діленням відповідної ЕРС на сумарний опір, який враховує опір датчика, приймача та лінії зв’язку, тобто:
де
Якщо rп=rд=r,а xп=xд=x, то:
де
Оскільки в співвідношеннях (16.17) всі ЕРС мають однакову часову фазу, у подальшому замість векторів будемо оперувати скалярними величинами. Тоді струми в лініях зв’язку за формулою (16.18):
Сума струмів:
при будь-яких значеннях θд й θ, тобто необхідності в нульовому дроті (рис.16.5) немає. Рівняння (16.25) підтверджують властивість самосинхронізації сельсинів при р=1 в межах одного оберту, оскільки струми в променях обмотки синхронізації дорівнюють нулеві лише при θ=0 й θ=360º. Струми променів обмотки синхронізації створюють результуючу МРС, просторовий напрям якої залежить від положення ротора. Ця МРС може бути розкладена за подовжньою й поперечною осями машини. При цьому:
Відповідно для датчика та приймача:
Відомо [1], що МРС фазної обмотки при синусоїдному розподілі дорівнює:
Оскільки в нашому випадку р=1, для променів обмотки синхронізації датчика та приймача за формулою (16.30):
Струми в обмотках синхронізації датчика та приймача проходять в різних напрямах. Тому:
Підставимо з (16.31) у (16.25) з урахуванням (16.29), (16.16), (16.32). Після перетворень одержимо:
Отже, подовжні складові МРС датчика та приймача мають негативний знак, тобто розмагнічують основне поле машини. Тому магнітний потік датчика Фg:
де Fдзб – МРС обмотки збудження; λd – магнітна провідність по подовжній осі. Поперечна МРС обмотки синхронізації не компенсується й створює потік поперечної реакції:
де λq – магнітна провідність по поперечній осі. МРС синхронізуючої обмотки дорівнює:
З формул (16.33)÷(16.36) видно, що Fd й Fq залежить тільки від θ й не залежать від θд й θп.
Рис. 16.6. Дія обмотки синхронізації по поперечній та подовжній осях машини
На рис.16.6 показана зосереджена обмотка одного променя обмотки синхронізації 1. Під дією змінного у часі потоку Фзб в обмотці 1 трансформується ЕРС та створюються струм і МРС F. Ця МРС може бути розкладена на поперечну і подовжню складові Fd та Fq, які створюють потоки Фd і Фq. Такому розкладанню відповідають дві обмотки 2 і 3, розташовані по осях машини (2 – по подовжній, 3 – по поперечній). Взаємодія Іq й Фd (Fq й Фd) створює одну складову синхронізуючого моменту, а Іd й Фq (Fd й Фq) – іншу. Оскільки зусилля Qd й Qq спрямовані в різні боки, складові моменту віднімаються. При малих θ й нерухомому роторі Fd≈0. Тому Qd≈0 й миттєве значення синхронізуючого моменту наближено можливо підрахувати, як
Синхронізуючий момент визначається, як векторний добуток двох зсунутих між собою на кут θ просторових векторів потоку й МРС, які створюються змінним струмом і тому є величинами, які залежать від часу. Тому й момент залежить від часу. З формули (16.40) після перетворень одержимо:
де ψ – головний кут зсуву фаз між векторами Середнє за період значення синхронізуючого моменту датчика:
Аналогічний вираз, але з іншим знаком, можливо одержати й для сельсина-приймача. Тому в подальшому індекс «д» в формулах для моменту не застосовуємо:
Рис. 16.7. Векторна діаграма для датчика
У відповідності з рис.16.7 Cosψ=Sinφ, тому:
Оскільки магнітний ланцюг машини не насичений, можливо записати:
Крім того, у відповідності з (16.31)
З формули (16.44) з урахуванням (16.45)÷(16.48):
де
Найбільша величина Мстах виникає при Судячи з формули (16.49), коливання мережевої напруги значно впливають на величину Мстах. Тому їх обмежують величиною ±10% від Uн.
Рис.16.8. Вплив поперечного потоку на кутову характеристику Якщо у відповідності з (18.42) побудувати графік Мс(θ), то це буде крива 1 рис.18.8. В реальних сельсинах внаслідок того, що Fd≠0, x та r змінюються в залежності від θ, а крива Мс(θ) значно відрізняється від синусоїди (графіки 2,3). Для наближення кривої Мс(θ) до синусоїди компенсують потік Фq за допомогою короткозамкненої обмотки, вісь якої перпендикулярна до осі обмотки збудження. Компенсація Фq викликає збільшення Іq та, відповідно, Fq і Мс. Сельсини характеризуються питомим синхронізуючим моментом Мсп та початковою крутістю МS синхронізуючого моменту, поняття про які подано в розділі 12. Для збільшення Мсп при малих θ індикаторні сельсини виконують із зосередженого обмоткою збудження та явно вираженими полюсами. Реактивний момент, який при цьому з’являється, збільшує Мс на 10÷20%. Якщо сельсини працюють в режимі обертання, то Мс зменшується, оскільки в обмотках синхронізації наводяться додаткові ЕРС та струми обертовими магнітними потоками збудження датчика й приймача. Динамічний синхронізуючий момент можливо розрахувати за методом симетричних складових, але для практичних розрахунків користуються емпіричною формулою Еллера:
де
ωс – синхронна кутова швидкість при частоті ƒ; ω – кутова швидкість обертання ротора приймача. Формула Еллера дає досить точні результати при ν≤0.65 та θ=40º÷50º. При ν=0.1÷0.2 можливо з достатньою точністю вважати МД=Мс. Якщо сельсини працюють в динамічному режимі при змінній швидкості обертання, то виникають два явища, які негативно впливають на роботу синхронної передачі: механічні коливання ротора приймача біля заданого кутового положення та рознос. Явище розносу виникає при великих швидкостях заведення сельсина-датчика. При цьому в сельсині-приймачі виникає асинхронний момент, який може розігнати ротор до синхронної швидкості, внаслідок чого втрачається керованість приймача. Для усунення цих явищ застосовують два види демпфування: зовнішнє та внутрішнє. Внутрішнє електромагнітне демпфування здійснює короткозамкнена обмотка по поперечній осі. Зі збільшенням частоти мережі ефективність внутрішнього демпфування різко спадає. Тому в синхронних передачах з підвищеними частотами застосовують зовнішні магнітоелектричні механічні демпфери. Двоступінчастий інерційно-фрикційний демпфер виконується у вигляді маховичка з насадженим на нього ободом, який може обертатись незалежно від маховичка.
При великих прискореннях, коли виникають коливання ротора сельсина-приймача, зовнішній обід демпфера ковзає по центральній частині маховичка, створюючи демпфуючий момент тертя. При постійній швидкості обертання обід маховичка обертається сумісно з його центральною частиною. Тому розсіювання енергії у фрикційному зчепленні відсутнє.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.008 с.) |


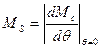 ;
; . (16.12)
. (16.12)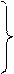 Якщо θд=θп=0, то, у відповідності з принципом дії сельсинної передачі, осі обмоток збудження та одного з променів обмотки синхронізації (на рис.16.5 – промінь А) співпадають. Це положення будемо вважати початком відліку. При цьому в променях А1 та А2 індуктуються найбільші ЕРС Еm. Якщо повертати обмотки збудження й синхронізації одну відносно одної, то ЕРС променів А1 та А2 будуть зменшуватись. Залежність ЕА1(θд) та Е2(θп) будуть гармонічними – косинусоїд ними. ЕРС в інших променях будуть у фазі з ЕА, але іншої величини, відповідної просторовому зсуву променів. У відповідності з цим для рис.16.5:
Якщо θд=θп=0, то, у відповідності з принципом дії сельсинної передачі, осі обмоток збудження та одного з променів обмотки синхронізації (на рис.16.5 – промінь А) співпадають. Це положення будемо вважати початком відліку. При цьому в променях А1 та А2 індуктуються найбільші ЕРС Еm. Якщо повертати обмотки збудження й синхронізації одну відносно одної, то ЕРС променів А1 та А2 будуть зменшуватись. Залежність ЕА1(θд) та Е2(θп) будуть гармонічними – косинусоїд ними. ЕРС в інших променях будуть у фазі з ЕА, але іншої величини, відповідної просторовому зсуву променів. У відповідності з цим для рис.16.5: ;
;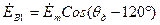 ; (16.13)
; (16.13)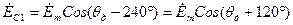 ;
;
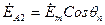 ;
; ; (16.14)
; (16.14) .
.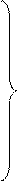
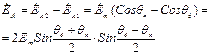 ;
; ; (16.15)
; (16.15)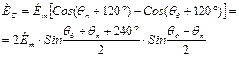 .
.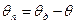 . (16.16)
. (16.16)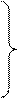
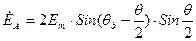 ;
;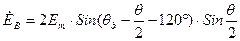 ; (16.17)
; (16.17)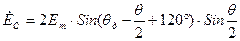 .
. , (16.18)
, (16.18)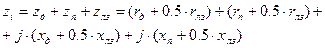 . (16.19)
. (16.19)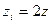 , (16.20)
, (16.20)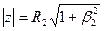 ; (16.21)
; (16.21)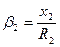 ; (16.22)
; (16.22) ; (16.23)
; (16.23)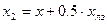 . (16.24)
. (16.24)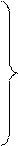
 ;
;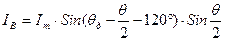 ; (16.25)
; (16.25) .
. (16.26)
(16.26)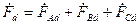 (16.27)
(16.27)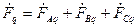 (16.28)
(16.28)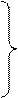
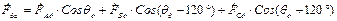 ;
;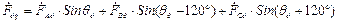 ;
;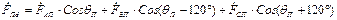 ; (16.29)
; (16.29)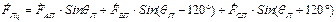 .
.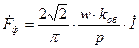 . (16.30)
. (16.30)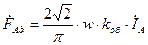 ;
;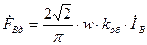 ; (16.31)
; (16.31)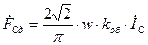 .
.
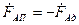 ;
; ; (16.32)
; (16.32)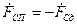 ;
;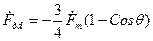 ; (16.33)
; (16.33) ; (16.34)
; (16.34)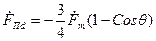 ; (16.35)
; (16.35)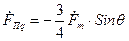 . (16.36)
. (16.36)
 , (16.37)
, (16.37)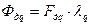 , (16.38)
, (16.38)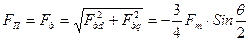 . (16.39)
. (16.39)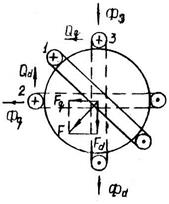
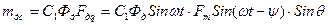 . (16.40)
. (16.40)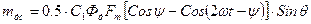 , (16.41)
, (16.41)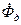 ,
, 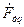 .
.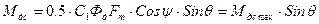 . (16.42)
. (16.42) . (16.43)
. (16.43)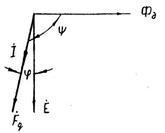
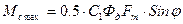 (16.44)
(16.44)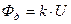 . (16.45)
. (16.45)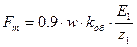 ; (16.46)
; (16.46) ; (16.47)
; (16.47) . (16.48)
. (16.48)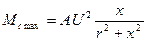 , (16.49)
, (16.49)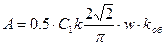 . (16.50)
. (16.50) , тобто r=x, φ=45º.
, тобто r=x, φ=45º.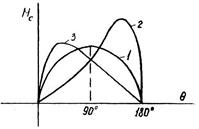
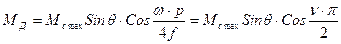 , (16.51)
, (16.51) – відносна швидкість обертання;
– відносна швидкість обертання;


