
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гаусса для вектора напряженности электрического поля. Применение теоремы для расчета полей бесконечной плоскости, нити, сферы, равномерно заряженного по объему шара.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электростатика как раздел физики. Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Изображения электрических полей. Электростатика – раздел физики, изучающий взаимодействие электрически заряженных частей в неподвижной данной системе отсчёта. Закон сохранения заряда: Алгебраическая сумма зарядов тел в изолированной системе остаётся постоянной при любых взаимодействий между телами.
Закон Кулона: Сила взаимодействия между двумя точечными зарядами прямо пропорциональна произведению зарядов тел, обратно пропорциональна квадрату расстояния между ними, направленна вдоль прямой соединяющей заряды. F = Напряжённостью электрического поля в данной точке пространства называется отношение силы действующей на заряд помещённой в данной точке пространства на этот самый заряд.
Напряжённость электрического поля, создаваемого системой электрически заряженных тел равна геометрической сумме напряжённостей, создаваемой телами системы по отдельности.
Изображение электрических полей: Силовой линией называется линия, касательная которой в каждой точке совпадает по направлению с вектором напряжённости электрического поля.
Свойства вектора напряженности: · Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. · Силовые линии не пересекаются. Густота силовых линий прямо пропорциональна вектору напряжённость. Поле диполя. Электрический диполь - это система из двух одинаковых по модулю разноименных точечных зарядов + q и - q, находящихся на некотором расстоянии l друг от друга. Диполь называют точечным, если расстояние от диполя до точки наблюдения значительно больше l.
Пусть l - вектор, проведенный от отрицательного заряда к положительному. Вектор p=ql называется электрическим моментом диполя или дипольным моментом. Потенциал поля диполя можно найти, используя принцип суперпозиции (φ=φ1+φ2+…. =Σφi) и формулу для потенциала точечного заряда.
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Поле диполя
Электрическое поле диполя можно найти в любой интересующей нас точке, опираясь на принцип суперпозиции. Напряженность поля в этой точке равна векторной сумме напряженностей, создаваемых точечными зарядами + q и — q: E ⃗ = E ⃗ ++ E ⃗ Диполь в электрическом поле На заряды диполя действуют равные по модулю, но противоположные по направлению силы которые стремятся развернуть диполь Относительно оси, проходящей через центр диполя каждая сила создает вращающий момент, равный произведению модуля силы на соответствующее плечо qE ⋅ l 2sin α Теорема Гаусса для вектора напряженности электрического поля. Применение теоремы для расчета полей бесконечной плоскости, нити, сферы, равномерно заряженного по объему шара. Теорема Гаусса для
α n
2) N=
Положительной в замкнутой пов-ти наз-ся Поток
Примеры применения Метода Гауссу 1)Поле бесконечно равномерно заряженной нити
4. Работа сил электрического поля. Циркуляция вектора E. Потенциал электрического поля. Работа сил электрического поля(Работа по перемещению заряда электрич. поля)
Независимость работы от формы траектории показывает,что сила Кулона является консервативной W=1/(4Пиε0)*Qq/R Независимость работы от формы траектории показывает,что сила Кулона является консервативной Теорема о циркуляции для вектора Е электростатического поля (Стокса)
ПРАВИЛА КИРХГОФА. Узлом электрич.цепи называется точка, в которой сходятся 3 и более проводника. 1 правило(правило узлов): алгебраическая сумма токов, сходящихся в узле равна нулю!(токи с разными знаками) Контуром называется любая замкнутая часть эл.цепи. 2 правило(правило контуров): алгебраическая сумма падения напряжений в контуре равна алгебраической сумме ЭДС, действующих в том же контуре
Эффект Холла. 1) Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле
Скорость электронов
Коэффициент 2)Напряжённость электрического поля (поля Холла) появление в проводнике с током плотностью j, помещенном в магнитное поле Н, электрического поля Ex, перпендикулярного Н и I. Напряжённость электрического поля (поля Холла) равна: Ex = Rhjsin a, (1) где a угол между векторами Н и f (a < 180°). Если H ^ j, то величина поля Холла E x максимальна: E x = RHj. Величина R, называется коэффициентом Холла, является основной характеристикой Магнитное поле в веществе
Диамагнетики – вещества незначительно ослабляющие магнитное поле. ᵡ≤0, 10^(-3) – 10^(-7) Парамагнетики – вещества незначительно усиливающие магнитное поле. ᵡ≥0, 10^(-4) Ферромагнетики – вещества значительно усиливающие внешнее магнитное поле. ᵡ˃˃1, ~10^5 Гипотеза Ампера Согласно гипотезе Ампера, внутри молекул и атомов циркулируют элементарные электрические токи. Сейчас мы уже знаем, что эти токи представляют собой движение электронов по орбитам в атоме. Если плоскости, в которых циркулируют эти токи, расположены беспорядочно по отношению друг к другу вследствие теплового движения молекул, составляющих тело, то их взаимодействия взаимно компенсируются и никаких магнитных свойств тело не обнаруживает. И наоборот: если плоскости, в которых вращаются электроны, параллельны друг другу и направления нормалей к этим плоскостям совпадают, то такие вещества усиливают внешнее магнитное поле. Ампер решительно отказался от представления о существовании в природе особых магнитных зарядов. Магнитные моменты атомов Магнитный момент единицы объёма вещества – намагниченность
Электростатика как раздел физики. Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Изображения электрических полей. Электростатика – раздел физики, изучающий взаимодействие электрически заряженных частей в неподвижной данной системе отсчёта.
Закон сохранения заряда: Алгебраическая сумма зарядов тел в изолированной системе остаётся постоянной при любых взаимодействий между телами.
Закон Кулона: Сила взаимодействия между двумя точечными зарядами прямо пропорциональна произведению зарядов тел, обратно пропорциональна квадрату расстояния между ними, направленна вдоль прямой соединяющей заряды. F = Напряжённостью электрического поля в данной точке пространства называется отношение силы действующей на заряд помещённой в данной точке пространства на этот самый заряд.
Напряжённость электрического поля, создаваемого системой электрически заряженных тел равна геометрической сумме напряжённостей, создаваемой телами системы по отдельности.
Изображение электрических полей: Силовой линией называется линия, касательная которой в каждой точке совпадает по направлению с вектором напряжённости электрического поля.
Свойства вектора напряженности: · Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. · Силовые линии не пересекаются. Густота силовых линий прямо пропорциональна вектору напряжённость. Поле диполя. Электрический диполь - это система из двух одинаковых по модулю разноименных точечных зарядов + q и - q, находящихся на некотором расстоянии l друг от друга. Диполь называют точечным, если расстояние от диполя до точки наблюдения значительно больше l.
Пусть l - вектор, проведенный от отрицательного заряда к положительному. Вектор p=ql называется электрическим моментом диполя или дипольным моментом. Потенциал поля диполя можно найти, используя принцип суперпозиции (φ=φ1+φ2+…. =Σφi) и формулу для потенциала точечного заряда.
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Поле диполя Электрическое поле диполя можно найти в любой интересующей нас точке, опираясь на принцип суперпозиции. Напряженность поля в этой точке равна векторной сумме напряженностей, создаваемых точечными зарядами + q и — q: E ⃗ = E ⃗ ++ E ⃗ Диполь в электрическом поле На заряды диполя действуют равные по модулю, но противоположные по направлению силы которые стремятся развернуть диполь Относительно оси, проходящей через центр диполя каждая сила создает вращающий момент, равный произведению модуля силы на соответствующее плечо
qE ⋅ l 2sin α Теорема Гаусса для вектора напряженности электрического поля. Применение теоремы для расчета полей бесконечной плоскости, нити, сферы, равномерно заряженного по объему шара. Теорема Гаусса для
α n
2) N=
Положительной в замкнутой пов-ти наз-ся Поток
Примеры применения Метода Гауссу 1)Поле бесконечно равномерно заряженной нити
4. Работа сил электрического поля. Циркуляция вектора E. Потенциал электрического поля. Работа сил электрического поля(Работа по перемещению заряда электрич. поля)
Независимость работы от формы траектории показывает,что сила Кулона является консервативной W=1/(4Пиε0)*Qq/R Независимость работы от формы траектории показывает,что сила Кулона является консервативной Теорема о циркуляции для вектора Е электростатического поля (Стокса)
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.012 с.) |

 = const
= const


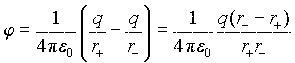
 электрического поля.
электрического поля. 1)
1)
 -полный поток
-полный поток




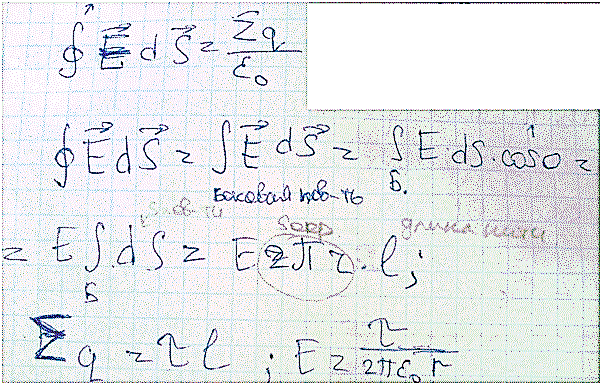
 2)Поле бесконечно равномерно заряженной плоскости
2)Поле бесконечно равномерно заряженной плоскости

 справа рисунок для записи справа
справа рисунок для записи справа Теорема Стокса математически отражает консервативность силы Кулона
Теорема Стокса математически отражает консервативность силы Кулона

 течёт электрический ток под действием напряжённости
течёт электрический ток под действием напряжённости  . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде. Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов  не скомпенсирует магнитную составляющую силы Лоренца:
не скомпенсирует магнитную составляющую силы Лоренца:
 можно выразить через плотность тока:
можно выразить через плотность тока: где
где  — концентрация носителей заряда. Тогда
— концентрация носителей заряда. Тогда 
 пропорциональности между
пропорциональности между  называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак
называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак  , что объясняется в полуклассической и квантовой теориях твёрдого тела.
, что объясняется в полуклассической и квантовой теориях твёрдого тела.
 (аналог вектора поляризации в электростатике)
(аналог вектора поляризации в электростатике)




