
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловая мощность тока-количество теплоты,выделяемое в проводнике в ед.времениСодержание книги
Поиск на нашем сайте
ПРАВИЛА КИРХГОФА. Узлом электрич.цепи называется точка, в которой сходятся 3 и более проводника. 1 правило(правило узлов): алгебраическая сумма токов, сходящихся в узле равна нулю!(токи с разными знаками) Контуром называется любая замкнутая часть эл.цепи. 2 правило(правило контуров): алгебраическая сумма падения напряжений в контуре равна алгебраической сумме ЭДС, действующих в том же контуре
Закон Био–Савара-Лапласа. Применение закона Б. С. Л. к расчету поля прямого проводника. Магнитное поле движущегося заряда. Закон Био–Савара-Лапласа определяет индукцию магнитного поля создаваемое проводником бесконечно малой длины.
Применение закона Б. С. Л. к расчету поля прямого проводника.
Магнитное поле движущегося заряда.
Магнитный момент контура. Поле на оси кругового контура с током.
Теоремы Гаусса и Стокса (поток и циркуляция) для вектора B. Расчет поля бесконечного соленоида и тороида. Циркуляция магнитного поля (закон полного тока) в вакууме. Теорема Гаусса для магнитного поля
1) Теорема о циркуляции для магнитного поля в вакууме Циркуляция вектора магнитной индукции поля в вакууме равна алгебраической сумме токов, охватываемых этим контуром (т. е. результирующему току через поверхность, опирающуюся на контур L), умноженной на магнитную постоянную:
Силовые поля, для которых циркуляция силового вектора отлична от нуля, называются вихревыми или соленоидальными. Магнитное поле является вихревым, а его силовые линии (линии вектора 2) Расчет магнитного поля токов. Используя теорему о циркуляции, можно рассчитывать магнитные поля токов, обладающие определенной симметрией, например, индукции магнитных полей внутри тороида и бесконечно длинного соленоида. Для соленоида: В = m0·nI;
для тороида:
где n - число витков на единицу длины соленоида; N - полное число витков тороида; r - радиус окружности, лежащей внутри тороида; R1 и R2 - внутренний и наружный радиусы тороида.
3) Теорема Гаусса для магнитной индукции
Элементарным потоком магнитной индукции(магнитнымпотоком)сквозь малую поверхность площадью dS называется физическая величина, равная
Магнитный поток сквозь произвольную поверхность S (рис. 2.11)
Если магнитное поле однородное, а поверхность S плоская, то
Ф m=Вn×S = B×S cos(
Единица измерения магнитного потока в СИ - 1 Вб (вебер). Теорема Гаусса для магнитного поля (силовые линии поля замкнуты)
4) Теорема Стокса §Bdl=µ∑I Циркуляция вектора магнитной индукции прямо пропорционально алгебраической сумме токов охватывающих контур интегрирования. §Bdl=µ( Положительными считаются токи связанные с обходом правилом правого винта
Эффект Холла. 1) Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле
Скорость электронов
Коэффициент 2)Напряжённость электрического поля (поля Холла) появление в проводнике с током плотностью j, помещенном в магнитное поле Н, электрического поля Ex, перпендикулярного Н и I. Напряжённость электрического поля (поля Холла) равна:
Ex = Rhjsin a, (1) где a угол между векторами Н и f (a < 180°). Если H ^ j, то величина поля Холла E x максимальна: E x = RHj. Величина R, называется коэффициентом Холла, является основной характеристикой
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.99.39 (0.009 с.) |







 .
. ) - замкнуты.
) - замкнуты.
 ; R2< r <R1,
; R2< r <R1,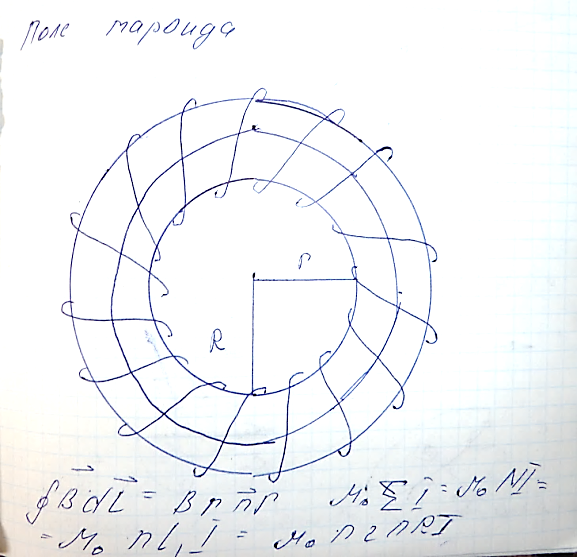


 .
. .
. ^
^  ).
). )
) течёт электрический ток под действием напряжённости
течёт электрический ток под действием напряжённости  . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде. Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов  не скомпенсирует магнитную составляющую силы Лоренца:
не скомпенсирует магнитную составляющую силы Лоренца:
 можно выразить через плотность тока:
можно выразить через плотность тока: где
где  — концентрация носителей заряда. Тогда
— концентрация носителей заряда. Тогда 
 пропорциональности между
пропорциональности между  называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак
называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак  , что объясняется в полуклассической и квантовой теориях твёрдого тела.
, что объясняется в полуклассической и квантовой теориях твёрдого тела.


