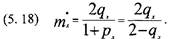Дитяча смертність (смертність немовлят)

Із ряду ймовірностей смерті (^) особливе значення має (qi,) як міра смертності дітей до одного року, або дитячої смертності.

Дитяча смертність вимірюється ймовірністю смерті новонародженого протягом року (першої о року після народження).

Поряд із (qo), яка охоплює увесь перший рік життя, у демографії розглядається перинатальна (утробна) смертність у перші дні після народження, які подаються відповідними ймовірностями.

3. Розподіл за тривалістю життя

Різниця двох чисел доживаючих /д та Іу (х<у) - то є відносне число помираючих (із новонароджених) у віковому інтервалі від х до у. Іншими словами, це відносна частка тих, чия тривалість життя лежить у тому ж інтервалі. Зокрема для однорічного інтервалу (х, д-+ 1) тривалості життя така частка складе:

(5,3) ^-/,-/„/.

Числа називаються числами помираючих. Число d, е ймовірність для новонародженого прожити від х до x+J років. Числа dx дають частоти розподілу за тривалістю життя (за однорічними інтервалами).

Оскільки:

/„=0 (vr - граничний вік), то:

"Всі люди смертні - сума чисел вичерпує усю сукупність народжених. Цей розподіл має вигляд, показаний на рис-4. Площа під кривою d^ дорівнює одиниці. Числа доживаючих /^ пов'язані простим співвідношенням з кумулятою того ж розподілу. Так, d„'=l-¹!; d, = // -І,... і чого видно, що:

(5.5) do+d,+...+d^\-h. Таким чином, /, є доповненням до 1 цієї кумуляти.

Щоб одержати лінію останньої, достатньо на рис.З вести відлік не знизу вгору від О до 1, а згори вниз (тобто для одержання її

зображення у звичному вигляді слід перекинути креслення і розглядати його у дзеркалі).

4. Тривалість життя

Оскільки існує розподіл за тривалістю життя, то можна говорити про його середню величину, тобто середню тривалість життя; про його моду ("нормальну" тривалість життя), про його медіану ("ймовірну"

тривалість життя).

Середня тривалість життя згідно даного порядку вимирання, є зважена за ймовірностями середня його можливих значень від 0 до w.

Наближено, якщо взяти за значення тривалості життя середини річних інтервалів для всіх помираючих у цьому віковому інтервалі, ця середня складе:

(у таблицях смертності, що публікуються найчастіше позначається

о\ Єа>-

Звідси:

(5.7)

Точний вираз для еу можна одержати, якщо від однорічних інтервалів перейти до безконечно малих. Із сказаного про 1„ як доповнення до 1 кумуляти розподілу за тривалістю життя виходить, що густота розподілу в інтервалі від х до x+ds (тут d, - звичайний диференціал віку) дорівнює [-/'(-с)]. Знак "мінус" зумовлений тим, що 1(х) є "перекинутою" кумулятою. Помноживши цю густоту на відповідне значення аргументу х та інтегруючи, одержимо:

о (замість w пишемо оо на верхній межі). Інтегруючи по частинах, маємо:

Але для х-0 маємо хі(х)=0»1=0, а для х (яке перевищує максимально можливу тривалість життя), по-суті, уже для x=~w маємо xl(x)= w0=0. Таким чином, перша складова відпадає і залишається:

На рис.З цьому відповідає площа між лінією дожиття і віссю х. Розбивши весь інтервал від 0 до w на однорічні, подамо eg у вигляді:

де L, - інтеграл по однорічному інтервалу від х до х+1. Якщо взяти N народжених, при даному порядку вимирання, то з них у віковому інтервалі (х, x+dx) будуть жити Nl(x). У цьому інтервалі

вони проживуть Nl(x)dx людино-років. А у річному інтервалі {х, x+dx)

*+і одержимо для них \Nl(x)dx років.

х

У середньому на одного народженого це дає L, людино-років у інтервалі (х. x+dx).

Середня тривалість життя ео є середнє число років, яке при даному порядку вимирання належить прожити народженому. Середня тривалість життя для осіб, що досягай віку х, складається із х уже прожитих років і середньої тривалості майбутнього життя для віку х, яка позначається Су Для її розрахунків слід відкинути із загального життя людино-років частину, прожиту до віку х, тобто взяти:

Ділити цю суму слід на число осіб, що досягли віку х, тобто 4. Одержимо:

Звідси можна одержати рекурентне співвідношення для перех до середньої тривалості майбутнього життя у наступній віковій групі. Оскільки 7,4 i-T^-L,=L,e,-L„

З переходом від х до х+1 середня тривалість майбутнього життя зменшується менше, ніж на 1 рік: відпадають померлі у річному інтервалі (х, х ¹ -7), тобто хто вступив у цей інтервал, але чия тривалість життя менша, ніж у інших. Внаслідок цього середня тривалість майбутнього життя у тих, хто залишився до віку х+1 може виявитись більшою, ніж Єх. Останнє явище при значній дитячій смертності проявляється у перших дитячих вікових групах. Віднімаючи, знаходимо (враховуючи, що 7-Р^оЛ:

Оскільки q^ - малий дріб, a ~" мало відрізняється від одиниці, ця різниця, як правило, від'ємна. Але, наприклад, для х=0 маємо:

Ця величина позитивна, якщо а =~°-, тим більше, якщо q = —.

la Єо

Наприклад, середня тривалість життя дорівнює 68,6 року. Звідси — = 0.016. Дитяча смертність дорівнює 0,0406. Це значно перевищує 0,016,

Єа

а тому, як видно з табл.З, е і =70,5, тобто більше й'о=68,6.

Парадокс дитячої смертності: у міру збільшення віку середня тривалість майбутнього життя у ранніх вікових групах не зменшується, а навпаки,зростає. Числа L, у багатьох демографічних розрахунках мають самостійне значення. Вони називаються числами живих (точніше, числами живих у стаціонарному населенні).

Якщо N народжених мають у віковому інтервалі (х, х + /) прожити Nl(x) людино-років, то оскільки цей інтервал дорівнює року, таке ж буде в середньому число їх при проходженні цього інтервалу. А у розрахунку не на N, а на 1 народженого це дасть Ly Так пояснюється назва цих чисел як чисел живих.

Крім середньої тривалості майбутнього життя, для кожної вікової групи Х можна вирахувати моду і медіану. Так, якщо за таблицями дожиття для жінок цією модою є вік 81 рік, то для всякого х<81 нормальна тривалість їх майбутнього життя дорівнює 81-х, а для х>81 його визначення втрачало зміст.

Ймовірна (медіанна) тривалість майбутнього життя у віковій групі Х дорівнює різниці між даним віком, і тим, до якого число доживаючих зменшиться удвоє. Так за таблицями (для чоловіків і жінок разом) для віку 70 років маємо: lw=0,6176; а половина цього числа 0,3088 співпадає з Is:. Отже, для х=70 ймовірна тривалість майбутнього життя дорівнює 82-70= 12 рокам.

Середню тривалість життя не можна змішувати із середнім віком померлих, та із середнім віком живих. Середній вік живих значною мірою визначається коливаннями рівня народжуваності, що до тривалості життя взагалі не має відношення. Якби не було ніякої варіації тривалості життя, середній вік живих був би, звичайно, набагато нижчим середньої тривалості життя. Теоретично, при наявності варіації, не виключений і випадок, коли середній вік живих перевищує середню тривалість життя. Це може трапитись при дуже високій дитячій смертності.

5. Табличний коефіцієнт смертності і сила смертності Ймовірність померти протягом року q, можна розглядати як відносне зменшення числа доживаючих при переході від віку х до віку х+1:

Якщо уявити собі річний інтервал, необхідний для такого переходу, то 1, - число живих на початок інтервалу. Але для виміру рівня смертності у звичайному демографічному значенні число смертей має бути віднесено не до початкової, а до середньої чисельності тих, що жили у цьому інтервалі. І.11я середня є Ly Якщо ми віднесемо до неї число смертей, одержимо табличний коефіцієнт смертності:

Зокрема, якщо вважати, ay>Lx=0.5(l^+l^i), то маємо наближено

Поділивши чисельник і знаменник на 0,5!^ одержимо:

Тут обидва показники: ймовірність q^ та коефіцієнт ^" відображають річний підсумок смертності. Але ж її рівень протягом року змінюється.

Більш точним мірилом була б смертність за якусь частину року Лх. Нагадаємо, що поділом на йх її слід було б привести до року. За інтервал від х до х+Ах маємо 1(х)-1(х+Ах) смертей із 1(х) тих, хто досяг цього інтервалу. Іншими словами, приведена до року ймовірність смерті у цьому інтервалі для тих, хто у нього вступив, дорівнює:

Щоб повністю виключити зміни смертності всередині взятого інтервалу і зробити показник таким, що строго характеризує точний вік х, потрібно 4х зробити безкінечно малою, тобто замінити на dx.

Приведена до року ймовірність смерті у безкінечно малому інтервалі віку (для тих, хто досяг його початку) називається силою смертності та позначається и(х):

тобто взятій зі знаком мінус логарифмічній похідній числа дожи-заючих.

Важливо відмітити, що для безкінечно малого вікового інтервалу dx шикає різниця між віднесення числа смертей до початкового чи до переднього числа живих у віковому інтервалі.

Оскільки у рамках однорічного інтервалу 1(х) змінюється дуже мано, то можна прийняти й ^т,-

У практичних розрахунках і та, й інша величина часто приймаються рівною коефіцієнту смертності даної вікової групи на основі зезпосередніх статистичних даних.

6. Таблиці смертності і реальне покоління

Показники таблиць смертності, про які ми говорили раніше, були розгорнуті, починаючи з ймовірностей q,. На повну реалізацію порядку вимирання, що випливає з цих таблиць, потрібно w років, де w - не менше 100. Протягом такого терміну рівень смертності не може залишитись незмінним. Отже, той що випливає з даних q, порядок не може здійснюва-гись у безпосередньому вигляді протягом життя якого-небудь реального покоління народжених. Це покоління, проходячи різні вікові етапи дає під вплив умов, що визначають рівень смертності у різні періоди.

Так, із тих, хто народився в Україні у 1900 p., частина на першому році життя підпадала під рівень дитячої смертності 1900р. і померла. Для живих цього покоління випали 1914-1921рр. - роки війни, розрухи, епідемії висипного тифу, голоду, громадянської війни. Далі настала колективізація 1929-1932 pp., голодомор 1933 p., репресії 1937-1939 pp., друга світова війна 1941-1945 pp., голод 1948 p., Чорнобильська катастрофа 1986 p., поразка СРСР у холодній війні і, як наслідок, розпад СРСР, зміна соціально-економічного ладу, утворення незалежної України та економічна криза 1990-1998 pp. Зрозуміло, що ці події впливали на смертність даного покоління.

Отже, порядок вимирання реального покоління не може

характеризувати закономірностей смертності.

У демографічній літературі про таблицю смертності реального покоління говорять, що вона побудована прямим методом, або методом поздовжнього аналізу.

На відміну від неї таблиця, що відображає рівні смертності всіх

окремих вікових груп, що мали місце в один і той же період (проміжок часу), називається таблицею смертності умовного покоління, вона побудована непрямим методом, або методом поперечного аналізу смертності.

Значення цих термінів не слід перебільшувати: смертність різних вікових груп у даний час є не менш реальним, а може для існуючого населення навіть більш актуально значущим фактом, ніж порядок вимирання сукупності народжених в один і той же час ровесників. Адже якраз смертність умовного покоління і є адекватним відображенням існуючого рівня смертності та її закономірностей.

П. Лаплас у вступі до "Аналітичної теорії ймовірностей", прагнучи популярно пояснити суть порядку вимирання, говорить про нього так, наче б то він відносився до реального покоління. Тому з іменем П. Лапласа пов'язуються дійсні спроби подати у таблицях смертності порядок вимирання реального покоління.

7. Страхові та інші розрахунки на основі таблиць смертності

У страхових розрахунках можуть знайти застосування методи так званої потенційної демографії, тобто системи демографічних показників, у яких рахунок ведуть не в людях, а в людино-роках майбутньої тривалості

життя.

У цій своєрідній системі місце звичайного числа народжених N займає відповідне йому число людино-років життя (рівне Ney), місце чисельності населення - сума майбутніх його людино-років життя, тобто ^§, Є,

а

(де Sx - чисельність населення у віці х), а точніше, fs(x)e(x)dx.

п

У страхових розрахунках все це можна застосувати практично, оскі льки, укладаючи договір, наприклад, на довічне страхування, страхова організація може розраховувати на одержання внесків протягом часу, рівного середній тривалості майбутнього життя. у її фінансовому плані це не менш важливо, ніж число осіб, які роблять вн ески. Випадок же смерті застрахованого не тільки потребує виплати цією організацією страхової суми, але і позбавляє її прибутку, що дорівнює середній тривалості майбутнього життя для осіб у віці померлого, помноженій на щорічний внесок. Аналогічно можна робити розрахунки для інших потреб.

Глава 6. ШЛЮБИ 1 РОЗЛУЧЕННЯ

1. Спеціальні коефіцієнти шлюбності

Шлюби і розлучення є фактами соціальними. Те, що в одному суспільстві визнається шлюбом, у іншому може не визнаватися; є країни, де

взагалі нема поняття розлучення.

Всі спеціальні показники шлюбності слід розглядати окремо для

чоловіків і жінок.

З якого віку можна вступати до шлюбу, визначає закон. У різних

країнах цей показник коливається від 12 до 21 року, а у Китаї зараз взагалі ЗО років. Часто закон дозволяє деякі виключення, а місцеві звичаї роблять ці виключення більш або менш частими. Тому демографи опираються не на "законний" вік, а користуються умовною границею: 15 років для жінок

та 18 років для чоловіків.

Час-гота укладання шлюбів для різного віку різна, тому число шлюбів залежить від вікової структури населення.

Відношення середньорічного числа шлюбів, укладених у даному

віці, до середньої чисельності осіб даного віку, називають повіковим коефіцієнтом шлюбності, або іноді - приведеним числом шлюбів; їх обчислюють окремо для чоловіків і жінок, звичайно на 1000 осіб.

Для аналізу найчастіше використовуються повікові коефіцієнти,

середні для п'ятирічних або десятирічних інтервалів віку.

Сума однорічних повікових коефіцієнтів шлюбності дає сумарний

коефіцієнт шлюбності; для його одержання з коефіцієнтів для п'ятирічних (або десятирічних) інтервалів ці коефіцієнти попередньо

перемножують на величину інтервалу.