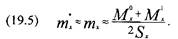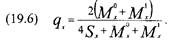Глава 19. Методи побудови демографічних таблиць

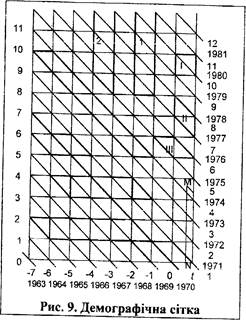
1. Демографічна сітка

Візьмемо прямокутну систему координат (рис.9).

Горизонтальну вісь назвемо віссю часу /, а вертикальну - віссю віку х. Року часу і року віку на обох осях повинні відповідати відрізки однакової довжини. Якщо з точок осі /, що відповідають початку кожного календарного року, провести прямі, паралельно осі х; а з точок осі х, що відповідають цілому числу прожитих років, провести прямі, паралельні осі t, то все координатне поле буде розбите на рівні квадрати.

Уявимо собі тепер життя кожної людини у вигляді вертикального відрізку, що починається у точці осі /, яка відповідає моменту його народження, та закінчується на висоті, що відповідає тривалості його життя, тобто точному вікові смерті. Це лінія життя людини. На малюнку лінія життя NM показує, що людина народилась 1 жовтня 1970 p. і померла у віці 3,5 p. (ці лінії на креслення не наносять, а тільки уявляють). Верхні кіпці ліній життя називають смертними точками. У проміжках між вертикалями сітки розміщені лінії життя і смертні точки всіх народжених у рамках відсічених вертикалями періодів.

Горизонтальні лінії сітки відмічають на лініях життя певний вік і називаються лініями віку.

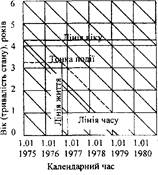
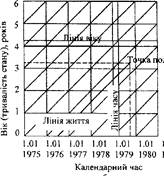
Кожна людина у деякий момент спостереження 7. має певний вік X. Якщо момент її народження є t, то, очевидно, що

(19.1) t+x=z, тобто дата спостереження дорівнює, даті народження плюс точний вік, відмічений у момент спостереження. Отже, смертні точки, розміщені між косими лініями сітки, відповідають смертям, що стались у відповідному проміжку часу. Косі лінії сітки називаються ізохронами. З допомогою ізохрони певний віковий момент на лінії житія автоматично перетворюється у календарний момент шляхом переносу відповідної точки з лінії життя по ізохроні на

вісь часу. На нашому малюнку, наприклад, видно, що дитині, яка народилась 1 жовтня 1970 p., виповнилось рівно 2 роки 1 жовтня 1972 p.; смерть її відбулась 1 квітня 1974 p., коли дитині було 3 роки 6 місяців.

Демографічну сітку запровадив В. Лексіс. З ЇЇ допомогою дуже просто вирішується ряд питань, які без неї можуть викликати часто здивування.

Наприклад, потрібно дізнатися, коли помруть діти, народжені у 1970 році, якщо смерть їх настане у віці 9 років (тобто від 9 до 10 років). Очевидно, всі смертні точки, про які іде мова, розміщені всередині квадрату І. Він обмежений двома прямими, з яких ліва відповідає 1 січню 1970 p., а права - 1 січню 1971 p. та двома горизонтальними прямими, з яких нижня відповідає віку 9 років, а верхня - віку 10 років. З малюнка видно, що цей квадрат охоплений двома ізохронами, з яких одна відповідає 1 січню 1979 p., а друга - 1 січню 1981 p. Значить, на запитання слід відповідати так: смерть дітей, що народились у 1970 p. і прожили 9 років, станеться між 1 січнем 1979 p. та 1 січнем 1981 p.

Друге питання; який вік смерті дітей, що народились протягом 1970 p. та померли протягом 1977 p.? Паралелограм II демографічної сітки зразу дає відповідь: вони померли у віці від 6 до 8 років.

Третє питання: у якому віці народились діти, які померли протягом 1975 p. у віці від 5 до 6 років? Розглянувши паралелограм ПІ, що відповідає умовам запитання, відповідаємо: ці діти народились у двохрічному проміжку між 1 січнем 1969 p. і 1 січнем 1971 p.

Отже, побудова демографічної сітки полягає у використанні трьох систем паралелей: ліній життя, ліній віку та ліній спостереження.

Слід зазначити важливе правило користування демографічною сіткою. Якщо взяти вертикальну смугу сітки, то через поступове вимирання людей з віком, число перетинання ліній життя з лініями віку та ізохронами буде зменшуватись, причому для будь-якої замкнутої фігури різниця між числом ліній життя, що входять до неї через її нижню границю, та числом ліній, які виходять з неї через верхню границю, дорівнює числу смертних точок, які розмістились всередині фігури.

Умовимося: під позначенням відрізка (або ламаної лінії) на демографічній сітці мати на увазі число ліній життя, що перетинають відрізок, а під позначенням замкнутої фігури - число смертних точок, розміщених у фігурі. Як координати точки на сітці будемо вказувати спочатку ізохрону, потім лінію віку, опускаючи між ними кому, там, де це не призведе до непорозумінь.

Число ліній життя, які перетинає ламана лінія, позначимо S з перерахуванням у дужках вершин цієї ламаної у вигляді пар координат, або їх позначень буквами.

Число смертних точок у певній фігурі позначимо М з переліком у дужках потрібних точок контуру.

Іноді вік будемо вказувати одним підрядковим індексом (наприклад, 3, тобто від х=3 до х=4), а номер ізохрони - надрядковим, маючи на увазі під ним її момент або рік, що ним закінчується.

Наприклад, 5'^(2.4;.5) або М{ 1,3; 2,3; 2,4; 1,4).

На лініях життя можна уявити й інші точки, наприклад взяття шлюбу, тощо. Число таких точок у певному контурі будемо позначати так, як і число смертних точок, але із заміною букви М на відповідне

Рис. 10. Демографічні сітки ВЛексіса (а) та Р.Пресса (б)

позначення подій.

Іншу, крім розглянутої вище сітки В.Лексіса, демографічну сітку запропонував французький демограф Ролан Пресса. Різницю між ними видно з наведеного рис. 10.

2. Сукупності живих і померлих

У демографічній статистиці виділяють дві основних сукупності живих.

Сукупність живих І роду складається з осіб, які народилися протягом певного проміжку часу і пережили певний вік х. Це - сукупність ровесників. На демографічній сітці сукупність живих І роду буде подана числом ліній життя, які перетинають відрізок лінії віку х (на рис.9 це 1=5(6,8; 7,8).

Сукупність живих її роду складається з осіб, які народилися у певному проміжку часу та пережили деякий календарний момент. На сітці ця сукупність подається числом ліній життя, які перетинають відрізок ізохрони (на рис.9 це 2= 5(5,8; 5,9). Це - сукупність сучасників. Вона одержується в результаті перепису населення, який дає чисельність сучасників на певний критичний момент з розподілом за роками народження та за віком.

При аналізі відтворення населення значну роль відіграють сукупності померлих. Розрізняють три сукупності.

Сукупність померлих 1 роду складається і осіб, які народилися протягом певного періоду і померли у певному інтервалі віку (на рис.9 це І-М(10,9; 11,10; 10,10; 9,9). На демографічній сітці ця сукупність складається із смертних точок, що лежать всередині певного прямокутника, сторони якого паралельні осям.

Сукупність померлих ТІ роду об'єднує померлих протягом певного часу із народжених за певний період. Графічно ця сукупність зображується числом смертних точок, розміщених всередині паралелограма, у якого дві сторони вертикальні, а дві інші - ізохрони (на рис.9 це ІІ=М(7,6; 8,7;

8,8; 7,7).

Сукупність померлих III роду об'єднує померлих протягом певного календарного періоду часу у певному інтервалі віку (на рис.9 це паралелограм ІП=М(6,5; 6,6', 5,6', 5,5). У цього паралелограма дві сторони -горизонтальні, а дві - ізохрони.

Всі вказані сукупності померлих можна скласти на сітці із прямокутних трикутників ч катетами, рівними одиниці (року). Смертні точки всередині цих прямокутників стононляті, елементарні сукупності померлих. Отже, елементарні сукупності померлих визначаються трьома ознаками: часом народження, часом смерті і піком смерті.

Щоб одержати у річній звітності елементарні сукупності, необхідно розподілити померлих протягом року за віком і всередині груп за иіком на дві підгрупи за роком народження.

3. Метод смертних списків

У побудові таблиць смертності використано багато методів і їх різновидів. Принципові відміни між ними: або характер використаних статистичних даних, або вихідний показник таблиць, на основі якого розраховуються всі інші.

У перших найпростіших таблицях вихідним показником були числа померлих dy Так були складені перші таблиці смертності Джоном Граун-том для Лондона, Едмундом Галлеєм для Бреславля, К.Ф.Германом для Росії.

За цим методом відношення числа померлих у віці х до загального числа померлих протягом певного періоду часу і є dy Якби числа народжень змінювалися лише внаслідок зростання населення при збереженні незмінних рівнів народжуваності і смертності, то вони зростали б разом з чисельністю населення у геометричній прогресії. Припустимо, що відомий знаменник цієї прогресії е". Тоді при відступі на один рік назад число народжень має ставати у е* разів меншим. Внаслідок цього при інших рівних умовах серед померлих осіб у віці х+1 повинно бути в е* разів менше, ніж у віці х. Звідси видно, що перед вирахуванням частот d, - числа помсрли\ М^ у кожному віці х мають бути помножені на е*¹. Одержимо для </, формулу:

Темп зростання населення k можна визначити як середній темп за чисельностями населення за якісь дві дати, бажано достатньо віддалені одна від одної.

4. Демографічний метод з вихідним w>

Використовуються дані про померлих за певний період у поєднанні з даними перепису про чисельність населення того чи іншого віку. Вихідним показником є табличний коефіцієнт смертності щ. Вважаємо, що він

дорівнює звичайному статистичному коефіцієнту смертності осіб даного віку ту Населення для обчислення т^ визначаємо, як чисельність його за переписом, приведену до середини періоду в таблиці. Далі обчислюємо ймовірність q,. Спосіб переходу від щ\ й ^ до ^ і далі до всіх інших показників залежить від способу визначення Ly

У найпростішому випадку виходять із L^^'^^l)> Що приведе до формули (5.18). З неї одержуємо:

(19.3) q =-^2W-.

" 2+W,

В інших випадках, приймаючи щ^Ц (середній силі смертності у віковому інтервалі х, х+1), одержуємо формулу:

(19.4) q^l-e-"'-. Нехай ми маємо за два роки числа померлих у віці х (див. рис.9) М°. ^та М\ ^\ ^сло живих у середині дворічного інтервалу у тому ж віці 5',. Оскільки М^М'. відноситься до дворіччя, то:

Використання у формулі (19.3) цього значення ^ дає формулу таблиць:

Відповідними методами будуються таблиці гіпотетичної шлюбності та народжуваності.

Всі вони передбачають певну політичну, соціальну й економічну стабільність у країні та відсутність зовнішніх впливів на ситуацію. Остання умова дуже проблематична у сучасному бурхливому світі. Все "•? і та дає побудові таких таблиць умовного, чисто теоретичного значення.