Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення координат точок за топографічною картоюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Ю.М. Панчук О.Є. Янчук
ЛАБОРАТОРНИЙ ПРАКТИКУМ З ІНЖЕНЕРНОЇ ГЕОДЕЗІЇ
Навчальний посібник
Рівне 2010 УДК 528.48(075) ББК 38.115 я 73 П 12 Затверджено вченою радою НУВГП. (Протокол № 11 від 04.11.2009 р.)
Рецензенти: Борисюк О.П., кандидат технічних наук, доцент кафедри інженерних конструкцій Національного університету водного господарства та природокористування; Романчук С.В., кандидат технічних наук, доцент кафедри землеустрою, геодезії та геоінформатики Національного університету водного господарства та природокористування.
Ю.М. Панчук, О.Є. Янчук П 12 Лабораторний практикум з інженерної геодезії. Навч. посібник. – Рівне: НУВГП, 2010. – 134 с.
У навчальному посібнику наведено основні відомості про лабораторні роботи і загальні вказівки щодо їх виконання, рішення типових задач за топографічною картою, вказівки з визначення площ контурів на планах і картах, будова і перевірки сучасних геодезичних приладів. Наведено методику кутових, лінійних і висотних вимірювань. Посібник містить практичні вказівки з побудови планового і висотного знімального обґрунтування, виконання топографічних знімань різними методами. Розглянуто питання складання поздовжнього профілю траси лінійних споруд і проектування на ньому. Посібник призначено для студентів вищих навчальних закладів, які навчаються за напрямами підготовки „Будівництво”, „Архітектура”, „Гідротехніка (водні ресурси)”, може стати у пригоді для студентів, які навчаються за напрямом „Гірництво”. Короткі відомості і вказівки щодо виконання польових робіт, які містяться в навчальному посібнику дозволять використовувати його при виконанні навчальної геодезичної практики. Табл. 10. Іл. 71. Бібліогр. 14 назв. УДК 528.48(075) ББК 38.115 я 73 © Панчук Ю.М., Янчук О.Є., 2010 © Національний університет водного господарства та природокористування, 2010 ЗМІСТ
Передмова........ 4 Робота №1. Визначення координат точок за топографічною картою....... 5 Робота №2. Рішення інженерних задач за топографічною картою 24 Робота №3. Вимірювання площ на топографічній карті полярним планіметром...... 36 Робота №4. Орієнтування ліній на топографічній карті. 46 Робота №5. Будова і перевірки нівелірів... 57 Робота №6. Побудова поздовжнього і поперечного профілів лінійної споруди..... 69 Робота №7. Нанесення проектної лінії на профіль.. 82 Робота №8. Геометричне нівелювання... 88 Робота №9. Будова теодоліта. Вимірювання кутів.. 94 Робота №10. Перевірки теодоліта 2Т30... 106 Робота №11. Обчислення координат точок теодолітного ходу 112 Робота №12. Камеральна обробка матеріалів тахеометричного знімання. Складання топографічного плану.. 121 Робота №13. Тригонометричне нівелювання.. 129 Література....... 134 ПЕРЕДМОВА
Лабораторний практикум з інженерної геодезії за змістом і послідовністю викладення в ньому матеріалу відповідає програмі курсу інженерної геодезії. Практикум містить вказівки з виконання лабораторних і розрахунково-графічних робіт, в ньому наведені основні відомості і вказівки з виконання польових робіт, що дозволяє використовувати даний посібник при проходженні навчальної геодезичної практики. Використовувати лабораторний практикум студенти повинні лише після вивчення теоретичного матеріалу курсу „Інженерна геодезія”. Суттєву увагу в лабораторному практикумі приділено будові, перевіркам і юстируванням геодезичних приладів. В кінці кожної лабораторної роботи наведені відповідні завдання на виконання роботи, а також контрольні питання для самостійного опрацювання матеріалу студентами, що дозволяє їм орієнтуватись в обсязі знань потрібних для успішного виконання лабораторних робіт і їх захисту. Основне призначення практикуму – закріплення теоретичних знань і активація творчої самостійної роботи студентів при виконанні лабораторних та розрахунково-графічних робіт, а також учбової практики. Особливу увагу звернено на рішення найбільш поширених в будівельній практиці інженерно-геодезичних завдань. Достатню увагу приділено організаційній частині проведених занять. З цією метою після завдань кожної роботи наводиться перелік необхідних приладів і пристосувань, що дозволяє студентам більш ретельно підготуватись до занять. Лабораторний практикум віддзеркалює досвід проведення лабораторних і розрахунково-графічних робіт на кафедрі землеустрою, геодезії та геоінформатики Національного університету водного господарства та природокористування. Лабораторні роботи №№ 1, 2, 3, 4, 9 і 10 написані Панчуком Ю.М., роботи №№ 5, 6, 7, 8 – написані Янчуком О.Є., роботи №№ 11, 12, 13 написані Панчуком Ю.М. і Янчуком О.Є разом. Комп’ютерний набір та верстка лабораторного практикуму виконано О.Є. Янчуком. Лабораторна робота 1. (2 год)
Рис. 1.9. Міжнародна розграфка листів карт масштабу 1:1000000
1.2. Горизонтальні проекції ліній місцевості на картах і планах зображують з деяким зменшенням. Ступінь зменшення ліній місцевості при перенесенні їх на папір називається масштабом. Масштаб – відношення довжини відрізка на карті до його горизонтального прокладення на місцевості. Масштаб топографічної карти можна представити відношенням:
де d – довжина відрізка на карті, D – горизонтальна проекція цього відрізка на місцевості. Масштаби можна умовно поділити на крупні та дрібні. Чим більший знаменник масштабу, тим дрібнішим вважається масштаб, і навпаки, чим менший знаменник масштабу, тим крупнішим є масштаб. Відстань на місцевості, яка відповідає 0,1 мм в масштабі карти, називають граничною точністю цього масштабу, або просто точністю масштабу. Так, при масштабі 1:25000 точність масштабу дорівнюватиме 2,5 м. Виходячи з цієї величини, можна зробити висновок: при складанні карти в масштабі 1:25000 на місцевості треба вимірювати відрізки (або предмети) довжиною не менше 2,5 м, оскільки менші розміри при цьому масштабі на карті показати неможливо. Маштаб виражають у числовій, словесній та графічній формі: · числовий масштаб являє собою дріб, у якого чисельник є одиниця, а знаменник – число, яке показує, в скільки разів зменшений відрізок місцевості, наприклад: 1:500, 1:1000, 1:2000, 1:5000, · словесний (мовний) масштаб – на планах і картах поряд із числовим масштабом також вказується скільком метрам на місцевості відповідає 1 см плану, наприклад при числовому масштабі 1:2000, словесний матиме вигляд: в 1 сантиметрі 20 метрів (рис. 1.10, б); · лінійний масштаб – являє собою шкалу у вигляді відрізку прямої, яка розділена на рівні частини (рис. 1.10, в). Такі рівні частини називають основами. Довжина основи може бути будь-якої величини, але найчастіше вона дорівнює 2 см. Першу зліва основу (її називають головкою масштабу) поділяють на 10 рівних частин. Після цього лінійний масштаб підписують залежно від числового масштабу.
Рис. 1.10. Масштаби: а) числовий; б) словесний; в) лінійний
Недоліком лінійного масштабу є його невисока точність. Вона дорівнює половині значення малої поділки головки масштабу. Масштаб підписують знизу по центру листа карти (позиції 14-16 на рис. 1.4). На картах вказують числовий, словесний та лінійний масштаби (в такому порядку як показано на рис. 1.10), а на планах лише числовий та словесний масштаби. Для підвищення точності робіт на карті застосовують поперечний масштаб (рис. 1.11).
Рис. 1.11. Поперечний масштаб
1.3. Віддаль АВ (горизонтальне прокладення на місцевості між точками А та В) на карті можна визначити використовуючи різні способи: · за числовим масштабом: міряємо лінійкою віддаль між точками АВ на карті в см (lАВ) і обчислюємо віддаль між точками на місцевості за допомогою знаменника числового масштабу М (щоб отримати віддаль на місцевості в метрах потрібно значення М підставляти в метрах, для цього знаменник числового масштабу ділиться на 100, наприклад для масштабу 1:2000 – М=20м) за формулою:
Наприклад: на плані масштабу 1:2000 довжина лінії становить 3,4 см, тоді віддаль, згідно формули (1.2) LАВ =3,4×20=68 м. · за лінійним масштабом: вимірюємо вимірником віддаль між точками АВ, потім встановлюємо вимірник на лінійний масштаб таким чином, щоб права голка вимірника потрапляла на цілу основу, а ліва голка – на розграфлені малі поділки. Віддаль дорівнює сумі цілих основ та малих поділок. Наприклад: в масштабі 1:50000 (рис. 1.12) виміряна лінія рівна 1 основі праворуч від нуля та 1,5 поділкам ліворуч від нуля, тоді лінія рівна 1,15 основи і в даному масштабі LАВ = 1,15×500×2=1150 м (на два домножуємо у випадку, коли одна основа лінійного масштабу рівна 2 см).
Рис. 1.12. Визначення довжини лінії за допомогою лінійного масштабу
· за поперечним масштабом: вимірюємо вимірником віддаль між точками АВ в основах лінійки поперечного масштабу (lАВ) і обчислюємо віддаль між точками на місцевості за допомогою знаменника числового масштабу (на два домножуємо у випадку, коли одна основа лінійки поперечного масштабу рівна 2 см) за формулою:
Віддаль між точками АВ в основах лінійки поперечного масштабу lАВ визначається наступним чином: праву голку вимірника встановлюємо на вертикальну лінію так, щоб ліва голка потрапляла на ліву (розграфлену) основу. Переміщуємо вимірник таким чином, щоб дві голки знаходились на одній горизонтальній лінії, до перетину лівої голки з похилою лінією (похила лінія називається трансверсаль). При цьому знімають відлік в основах, який складається з трьох частин: ціле число основ праворуч від нуля (на рис. 1.13 відлік рівний 3 основам), десяті частини беруться ліворуч від нуля по горизонталі (рівний 2) та соті частини – кількість вертикальних поділок (рівний 7), тобто весь повний відлік lАВ=3,27 осн. Підставивши цей відлік в формулу (1.3) отримаємо довжину лінії, наприклад для масштабу 1:2000 LАВ=3,27×2×20=130,8 м.
Рис. 1.13. Визначення довжини лінії за допомогою поперечного масштабу
· аналітичним способом: цей спосіб використовують коли є відомі координати двох точок. Віддаль обчислюється за формулою:
Відрізки ліній, які мають довжину більшу, ніж довжина лінійного, або поперечного масштабів, вимірюють частинами або „кроком” вимірника. Для цього розхилом циркуля беруть довжину, яка відповідає цілому числу основ і „крокують” нею по карті, при цьому відлічуючи кількість перестановок голки вимірника. Залишок менший від довжини вибраного кроку, визначають за масштабом звичайним способом. Обернені задачі, коли за відомою відстанню на місцевості необхідно відкласти віддаль на карті, вирішуються виходячи з тих самих формул: · за числовим масштабом: віддаль на карті в см обчислюється за формулою:
· за поперечним масштабом: віддаль на карті в основах лінійки поперечного масштабу обчислюється за формулою:
1.4. Для визначення прямокутних координат точки В на карті (рис. 1.14) з точки В опускають перпендикуляри на лінії координатної (кілометрової) сітки. Довжини перпендикулярів Dx та Dy вимірюють з точністю масштабу карти за допомогою лінійки поперечного масштабу. Повні координати т. В визначають за формулами:
де Dx, Dy – віддалі від точки до відповідно південної та західної сторін квадрату в метрах. Наприклад на рис. 1.14: – координати південно-західної вершини квадрату, в якому знаходиться задана точка В: – прирости Dx та Dy визначені за допомогою лінійки поперечного масштабу: Dx =3,71 осн; Dy =2,72 осн; – прирости Dx та Dy на місцевості: Dx=3,71×2×100=742 м; Dy=2,72×2×100=544 м. – повні координати, згідно формули (1.7), дорівнюють: xB=6066742 м; yB=4312544 м.
Рис. 1.14. Визначення прямокутних координат точок та нанесення точок за прямокутними координатами за топографічною картою масштабу 1:10000
1.5. Для того, щоб побудувати точку С за її прямокутними координатами, необхідно знайти квадрат, в якому знаходиться точка С, виділити початкові координати Наприклад: xC=6065427 м; yC=4313226 м. В масштабі 1:10000 лінії кілометрової сітки проведені через 1000 м. Шукаємо координату
В нашому прикладі Dx=427м і Dy=226м. Після чого перетворюємо величини Dx та Dy у відрізки, які відповідають масштабу карти: Dx=427/(2×100)=2,135 осн., Dy=226/(2×100)=1,13 осн. Виставляємо за допомогою лінійки поперечного масштабу розхил вимірника на відлік Dx=2,135 осн і відкладаємо цю величину по вертикалі вздовж лівого і правого боку квадрату в якому знаходиться потрібна точка. В результаті отримуємо точки „а” та „b” (рис. 1.14), сполучаємо їх лінією і в цьому напрямку від точки „а” відкладаємо Dy=1,13 осн. Отримана точка і буде точкою С з координатами xC=6065427м; yC=4313226м.
Приклади типових завдань. Завдання 1 За топографічною картою масштабу 1:10000 визначити відстані між точками А та В. Це виконати із застосуванням числового, лінійного і поперечного масштабів. Розташування точок А та В на топографічній карті задаються. Розв’язок: За числовим масштабом: вимірюємо лінійкою відстань між точками А та В на карті: lАВ=7,4 см; визначаємо значення знаменника числового масштабу: М=10000 см=100 м; обчислюємо відстань між точками А та В на місцевості (горизонтальне прокладання), за формулою (1.2): LАВ =lАВ×М(м)=7,4×100=740 м. За лінійним масштабом: вимірником вимірюємо віддаль між точками А та В, після чого встановлюємо вимірник на розграфлений лінійний масштаб таким чином, щоб права голка вимірника потрапляла на цілу основу, а ліва голка – на малі поділки. Відраховуємо кількість цілих основ праворуч від нуля: N1=3 основи; відраховуємо кількість поділок ліворуч від нуля: N2=7 поділок; обчислюємо відстань між точками А та В на карті в основах лінійного масштабу: lАВ =N1+ N2/10=3+7/10=3,7 осн; визначаємо значення знаменника числового масштабу: М=10000 см=100 м; обчислюємо відстань між точками А та В на місцевості (горизонтальне прокладання): LАВ =lАВ×2×М (м) =3,7 ×2×100=740 м. За поперечним масштабом: вимірником вимірюємо віддаль між точками А та В, після чого встановлюємо вимірник на розграфлений поперечний масштаб, як описано в питанні 3. Відраховуємо кількість цілих основ праворуч від нуля: N1=3 основи; відраховуємо кількість поділок по горизонталі ліворуч від нуля: N2=7 поділок; відраховуємо кількість поділок по вертикалі: N3=1 поділка; обчислюємо відстань між точками А та В на карті в основах поперечного масштабу: lАВ=N1+N2/10+N3/100=3+7/10+1/100=3,71 осн; визначаємо значення знаменника числового масштабу: М=10000 см=100 м; обчислюємо відстань між точками А та В на місцевості (горизонтальне прокладання), за формулою (1.3): LАВ=lАВ×2×М (м)=3,71×2×100=742 м. Завдання 2 За допомогою поперечного масштабу нанести на карту, масштабу 1:10000, лінію заданої довжини. Віддаль LАD від точки А до точки D рівна 916 м, напрямок на точку D задається. Розв’язок: Обчислюємо віддаль lАD на карті, в основах лінійки поперечного масштабу, за формулою (1.6): lAD=LAD /(2×M)=916/(2×100)=4,58 осн; виставляємо за допомогою лінійки поперечного масштабу розхил вимірника на обчислений відлік 4,58 осн і відкладаємо на карті від точки А в необхідному напрямку.
Завдання 3 Визначити прямокутні координати точки А за топографічною картою масштабу 1:10000. Розв’язок: Визначаємо координати лівої нижньої вершини квадрату в якому знаходиться точка А:
Визначаємо прирости Dx та Dy за допомогою лінійки поперечного масштабу: приріст Dxосн на карті, в основах поперечного масштабу (відстань від точки А до південної сторони квадрата): Dхосн = 2,47 осн; приріст Dхм на місцевості, в метрах: Dхм=Dхосн×2×М (м)= =2,47 ×2×100=494 м; приріст Dyосн на карті, в основах поперечного масштабу (відстань від точки до західної сторони квадрата): Dyосн=4,15 осн; приріст Dyм на місцевості в метрах: Dyм=Dyосн×2×М (м)= =4,15×2×100= =830 м. Обчислюємо координати точки А, за формулою (1.7):
Завдання 4 Нанести на топографічну карту масштабу 1:10000 точку С, за відомими прямокутними координатами: xc=5419136 м, yc=4625517 м. Розв’язок: Визначаємо координати південно-західної вершини квадрата в якому знаходиться точка С (мають бути кратними величині, через яку проведені лінії кілометрової сітки):
Визначаємо прирости Dxм та Dyм в метрах, за формулою (1.8):
Визначаємо прирости Dхосн і Dуосн на карті, в основах поперечного масштабу: Dхосн=Dхм /(2×М)=136/(2×100)=0,68 осн; Dуосн=Dум /(2×М)=517/(2×100)=2,58 осн. Відкладаємо обчислене значення Dхосн по вертикалі вздовж лівого і правого боку квадрату, в якому знаходиться потрібна точка. За напрямком двох отриманих точок відкладаємо Dуосн (від лівої отриманої точки). В результаті отримуємо точку С з координатами xc=5419136 м, yc=4625517 м.
Завдання 5 Визначити віддаль між точками А та С графічним (поперечний масштаб) та аналітичним способами. Для обчислення відстані аналітичним способом необхідно знати прямокутні координати точок А та С. Тому використаємо координати точки А визначені в завданні 3 та координати точки С задані в завданні 4. Розв’язок: За поперечним масштабом: вимірюємо відстань між точками А та С на карті в основах поперечного масштабу: lАС= 4,70 осн; обчислюємовідстань між точками А та С на місцевості, за формулою (1.3): LАС= lАС×2×М (м) = 4,70×2×100=940 м. Аналітичним способом: обчислюємо віддаль між точками А та С, в метрах, за формулою (1.4) (координати підставляються в метрах):
= =
Контрольні запитання:
Лабораторна робота 2. (2 год) Завдання 1 За топографічним планом визначити висоти точок D та P1 (рис. 2.7, а) (P1 – на горизонталі, D – між горизонталями). Розв’язок: а) визначаємо січення горизонталей на плані: h=1 м; знаходимо найближчу підписану горизонталь, її висота Н=150,00 м; за бергштрихами визначаємо в який бік висоти зростають; визначаємо висоту горизонталі на якій знаходиться точка P1, а отже й висоту точки P1: НP1=Нгор=149,00 м. б) відповідно до рис. 2.3 проводимо через точку D найкоротшу лінію між сусідніми горизонталями і вимірюємо її довжину d=7 мм; вимірюємо на плані відстань від горизонталі з меншою висотою до точки D: a=3 мм; визначаємо січення горизонталей на плані: h=1 м; визначаємо висоту меншої горизонталі Нгор=149,00 м; обчислюємо висоту точки D:
Завдання 2 Визначити крутизну схилу між точками за лінією OO1 (рис. 2.7, а) (між точками О-O1, О-1, 7-O1 за формулою (2.4), а між відрізками лінії 1-2, 2-3, … – за масштабом закладень). Розв’язок: Сполучаємо точки О та O1 прямою лінією. Точки перетину лінії OO1 з горизонталями нумеруємо 1, 2, 3, …, 7. Примітка: у випадку, коли лінія OO1 перетинає лінію водорозділу (водозбору), то в найвищій (найнижчій) точці ставиться додаткова точка, яка також нумерується. В даному випадка лінія OO1 перетинає котловину в найнижчій точці, яку позначимо 4. Визначаємо загальний ухил по лінії OO1, за формулою (2.4):
де НО, НО1 – висоти точок О та О1, м;
Аналогічно визначаємо ухил за всіма відрізками, перевищення між якими не дорівнює висоті перерізу рельєфу:
Ухил між точками, що знаходяться на горизонталях визначається за допомогою масштабу закладень, який необхідно побудувати. За формулою (2.5) обчислюємо закладення для заданих ухилів:
За обчисленими значеннями закладень на карті будуємо масштаб закладень. Для визначення ухилів, за побудованим масштабом закладень, беремо в розхил вимірника відстань між точками О та 1 і прикладаємо до перетину з масштабом закладень (як показано на рис. 2.6). Знак перед ухилом ставимо „+” – якщо кінцева точка лінії вище за початкову, та „-” – якщо кінцева точка нижче ніж початкова. Аналогічно визначаємо ухили між всіма точками, перевищення між якими рівне перерізу рельєфу: і 1-2=-0,050; і 2-3=-0,042; і 5-6=+0,026; і 6-7=+0,028; Завдання 3 Побудувати лінію АB з ухилом, що не перевищує 0,03. Розв’язок: Обчислюємо величину закладення на місцевості:
де h – висота перерізу рельєфу, м; і=0,03 – заданий ухил. Обчислюємо величину закладення на плані масштабу 1:2000: dгран=33,33/20=1,67 см. Подальший принцип побудови описаний в питанні 3.
Завдання 4 Побудувати профіль за лінією АВ. Розв’язок: Принцип побудови описаний в питанні 4.
Контрольні запитання: 1. Абсолютні і відносні висоти точок. 2. Рельєф місцевості, горизонталь, висота перерізу рельєфу, закладення. 3. Крутизна схилу місцевості. 4. Побудова масштабу закладень, визначення ухилів за ним. 5. Побудова профілю за заданим напрямком. Лабораторна робота 3. (2 год) Вимірювання площ на топографічній карті полярним планіметром 3.1. Будова полярного планіметра. 3.2. Визначення ціни поділки планіметра. 3.3. Визначення площі ділянки на карті полярним планіметром. Прилади і обладнання: топографічна карта, полярний планіметр, калькулятор, лінійка, олівець, гумка.
Для вирішення різних практичних задач треба вміти обчислювати площі земельних ділянок за результатами вимірів на місцевості і на планах (картах). Залежно від розміру та форми ділянок і бажаної точності, площі можна визначати трьома способами: 1) аналітичним; 2) графічним; 3) механічним, які можна застосовувати в „чистому ” вигляді або у комбінації їх між собою. Аналітичний спосіб. Обчислення площ за координатами вершин полігону застосовується коли полігон має складну форму багатокутника, границі якого прямолінійні і відомі координати його вершин (рис. 3.1). Формула для визначення площі аналітичним способом має вигляд:
і читається так: подвійна площа багатокутника дорівнює сумі послідовних добутків абсцис (іксів) на різницю ординат (ігреків) наступної та попередньої вершин по відношенню до абсциси.
Рис. 3.1. До визначення площі аналітичним і графічним способами Або:
і читається так: подвійна площа багатокутника дорівнює сумі послідовних добутків ординат на різницю абсцис попередньої і наступної вершин по відношенню до ординати. При обчисленнях обов’язково враховуються знаки різниць координат. Результати обчислення площі за двома формулами мають бути однаковими. Цей спосіб є найбільш точним. Найзручніше обчислення виконувати у таблиці. Зразок відомості обчислення площі аналітичним способом наведено в табл. 3.1, в якій розглянутий приклад обчислення площі фігури зображеної на рис. 3.1.
Таблиця 3.1 Відомість визначення площі полігона за координатами його вершин
Графічний спосіб. Цим способом площі контурів обчислюють якщо границі прямолінійні і фігура ділянки має просту геометричну форму (трикутника, прямокутника, трапеції тощо). Визначивши за картою довжини необхідних елементів, за формулами відомими з геометрії та тригонометрії знаходять площі фігур. Якщо ділянка має складну форму, то її попередньо розбивають тонкими лініями на трикутники або інші прості геометричні фігури (рис. 3.1). Тоді площу ділянки S визначають як суму площ простих фігур: Точність визначення площ графічним способом залежить від точності вимірювання ліній на плані. Відомо, що відрізки прямої вимірюються на плані з точністю 0,1 мм незалежно від довжини ліній. Тому відносна помилка при вимірюванні коротких ліній буде більшою, ніж при вимірювання довгих ліній. Отже, фігури, на які поділяється полігон, повинні бути по можливості більшими, а план – у крупнішому масштабі. При цьому бажано в розрахунках у першу чергу використовувати лінії, довжина яких виміряна безпосередньо на місцевості. Для того, щоб уникнути грубих помилок і підвищити точність визначення площі, лінії вимірюють двічі з допустимою похибкою 1/200. До графічного способу відносять також визначення площ палетками. Палетки використовуються для визначення площ криволінійних контурів. Квадратна палетка – це сітка квадратів із стороною 0,1, 0,2, 0,4, 0,5 або 1 см, накреслена на прозорому матеріалі (технічній фотоплівці, органічному склі, восківці), або сітка паралельних ліній (лінійна палетка) чи точок (точкова палетка) накреслених на тому ж матеріалі через однакові відстані одна від одної. Квадратну палетку накладають на контур ділянки і підраховують кількість повних квадратів, що вміщуються в контурі. Із неповних квадратів, розміщених на периферії контуру на око складають цілі квадрати і визначають загальну кількість квадратів. Потім обчислюють площу одного квадрату у квадратних метрах (або гектарах) за масштабом плану. Добуток площі одного квадрату на кількість їх у даному контурі дасть площу всієї ділянки. Для обчислення площі ділянки за допомогою палетки з паралельними лініями треба знайти сумарну довжину середніх ліній у сантиметрах, за масштабом перевести її у метри і помножити на відстань між двома сусідніми паралельними лініями (h) також переведену у метри. Механічний спосіб. При цьому способі використовують спеціальний прилад – планіметр. Це механічний прилад, який дає можливість шляхом обведення контуру фігури будь-якої форми визначити її площу.
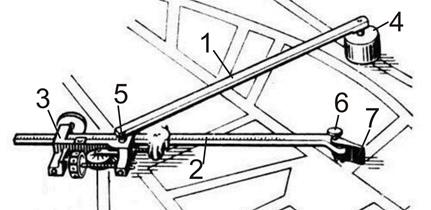
3.1. Планіметри бувають лінійні і полюсні (полюсний планіметр створений Я.Амслером (Німеччина) в 1854 році). Полюсні планіметри бувають з однією або двома каретками. Однокаретковий полюсний планіметр складається з трьох основних частин – полюсного (1) і обвідного(2) важелів та каретки (3) (рис. 3.2). Полюсний важіль являє собою металевий брусок квадратного перерізу, на одному з кінців якого закріплений тягарець з голкою, який називається полюсом (4) планіметра. Голка призначена для запобігання ковзанню полюса на карті. На другому кінці полюсного важеля знаходиться стрижень із кулеподібною головкою (5), який встановлюється в гніздо каретки обвідного важеля. Головка і гніздо утворюють шарнір, за допомогою якого з’єднуються важелі планіметру. Цей вузол служить віссю обертання обвідного важеля. Обвідний важіль зроблений з білого металу і має вигляд такого ж бруска, як і полюсний важіль. На одному кінці обвідного важеля змонтовано обвідний пристрій у вигляді тупого шпиля (6) або обвідного скельця в металевій оправі з точкою у центрі. Шпиль або точку обвідного скельця переміщують на плані (карті) за допомогою ручки (7), обводячи контур ділянки, площу якої необхідно визначити. На іншому боці обвідного важеля розміщується каретка, яка пересувається по ньому. Від відстані між кареткою і обвідним шпилем залежить ціна поділки планіметра.
Рис. 3.2. Будова полюсного планіметра
В каретці міститься відліковий механізм (рис. 3.3). Він складається з циферблата А, лічильного колеса В та верньєра С. Лічильне колесо переміщуючись на плані (карті) показує кількість поділок, пройдених ним під час обводу контуру фігури. Кількість повних обертів лічильного колеса відраховують за циферблатом, а його частин – за допомогою верньєра. У двохкареткових планіметрів марки ПП-2К (планіметр полярний двохкаретковий) на обвідному важелі змонтовано дві каретки однакової будови. Ціна поділки кожної з них різна. Під час вимірювань можна користуватися або лише однією з кареток, або двома, що робиться для контролю вимірювань. Відлік на лічильному механізмі складається із 4 цифр (рис. 3.3): першу цифру читають на циферблаті А проти нерухомого покажчика (індекса) D, причому знімають меншу з двох (на рис.3.3 – цифра 7). Другу цифру читають на барабані лічильного колеса В – це номер меншого підписаного штриха, найближчого до нуля верньєра (на рис.3.3 – цифра 3); третю цифру також відлічують на барабані лічильного колеса – це кількість не підписаних поділок від підписаного штриха до нуля верньєра лічильного механізму (цифра 1); четверту цифру читають на верньєрі С відлікового механізму – це номер поділки верньєра, рахуючи від нуля, яка точно співпадає з будь-якою поділкою на барабані лічильного колеса (цифра 5). Отже, остаточний відлік становить 7315.
Рис. 3.3. Знімання відліку за планіметром
Перевірки планіметра: 1) лічильне колесо повинно обертатися вільно без коливань; 2) відстань між барабаном лічильного колеса і дугою верньєра повинна бути мінімальною, не більше товщини листа паперу для записів; 3) площина лічильного колеса повинна бути перпендикулярною до осі обвідного важеля. Перевірка виконується вимірюванням площі ділянки при двох положеннях полюса. Умова виконана, якщо одержані результати не перевищують відносної помилки 1/250. Якщо похибка більша, то треба вико
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.018 с.) |

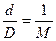 , (1.1)
, (1.1) (рис. 1.10, а);
(рис. 1.10, а);

 . (1.2)
. (1.2)
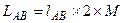 . (1.3)
. (1.3)
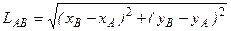 . (1.4)
. (1.4) ; (1.5)
; (1.5) . (1.6)
. (1.6) (1.7)
(1.7)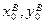 – координати південно-західної вершини квадрату, в якому знаходиться точка В;
– координати південно-західної вершини квадрату, в якому знаходиться точка В;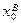 =6066000 м;
=6066000 м;  =4312000 м;
=4312000 м;
 i
i  (ці значення мають бути кратними величині, через яку проведені лінії кілометрової сітки), а також прирости Dx та Dy. Визначивши Dx та Dy у відрізках масштабу карти, наносять їх на координатну сітку і одержують точку С.
(ці значення мають бути кратними величині, через яку проведені лінії кілометрової сітки), а також прирости Dx та Dy. Визначивши Dx та Dy у відрізках масштабу карти, наносять їх на координатну сітку і одержують точку С. (1.8)
(1.8)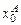 =5418 км =5418000 м;
=5418 км =5418000 м; =4624 км =4624000 м;
=4624 км =4624000 м;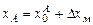 =5418000+494=5418494 м;
=5418000+494=5418494 м; =4624000+830=4624830 м.
=4624000+830=4624830 м. 5419136-5419000=136 м;
5419136-5419000=136 м;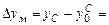 4625517-4625000=517 м.
4625517-4625000=517 м. =
= =
=  =
= =
= 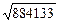 =940,28 м.
=940,28 м. =
= 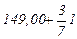 = 149,43 м.
= 149,43 м. =
= 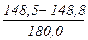 =-0,0017,
=-0,0017, – відстань між точками О та О1:
– відстань між точками О та О1:  ;
;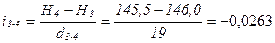 ;
; ;
; .
.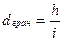 =
= 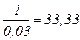 м,
м, , (3.1)
, (3.1)
 , (3.2)
, (3.2) . Для контролю площу обчислюють вдруге, використовуючи виміри інших елементів у тих самих фігурах.
. Для контролю площу обчислюють вдруге, використовуючи виміри інших елементів у тих самих фігурах.