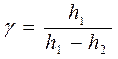Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення універсальної газової сталоїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторна робота №1 ВИЗНАЧЕННЯ УНІВЕРСАЛЬНОЇ ГАЗОВОЇ СТАЛОЇ МЕТОДОМ ВІДКАЧУВАННЯ Мета|ціль| роботи: визначити універсальну газову сталу. Обладнання: вакуумний насос, мановакуумметр|, барометр, термометр скляна куля, ваги з|із| важками. Теоретична частина Для вивчення фізичних властивостей макроскопічних систем, що складаються з великого числа часток|часток,часточок|, використовують два методи – статистичний і термодинамічний. Статистичний метод заснований на законах теорії вірогідності|ймовірності| і математичної статистики. Розділ теоретичної фізики, в якій вивчають фізичні властивості макроскопічних систем за допомогою статистичного методу, називається статистичною фізикою. Термодинамічний метод полягає у вивченні фізичних властивостей макроскопічних систем шляхом аналізу умов і кількісних співвідношень для процесів перетворення енергії в даних системах. Відповідний розділ теоретичної фізики називається термодинамікою, а макроскопічна система в термодинаміці - термодинамічною системою. Фізичні величини, що служать для характеристики стану термодинамічної системи, називають термодинамічними параметрами стану системи. До ним відносяться: об'єм|обсяг|, тиск|тиснення|, температура, концентрація і ін. Тиск|тиснення| - фізична величина Р, чисельно рівна силі, що діє на одиницю площі|майдану| поверхні тіла по напряму|направленню| нормалі до цієї поверхні:
де dFn – чисельне значення нормальної сили, що діє на малу ділянку поверхні тіла площею|майданом| dS. Складнішим і менш наочним|нагляднішим| є|з'являється,являється| параметр стану, званий температурою. Поняття температури має сенс тільки|лише| для рівноважних станів системи. Під рівноважним станом розуміють такий стан системи, який не змінюється з часом, причому ця постійність|незмінність| не пов'язана з протіканням якого-небудь процесу в зовнішньому середовищі|середі|. З молекулярно-кінетичної точки зору температура рівноважної системи характеризує інтенсивність теплового руху частинок|часток,часточок|. Абсолютна температура є|з'являється,являється| мірою середньої кінетичної енергії поступальної ходи молекул ідеального газу:
де k – постійна Больцмана. Простим об'єктом досліджень в термодинаміці і статистичній фізиці є|з'являється,являється| ідеальний газ. Ідеальним газомназивається газ, молекули якого мають малий власний об'єм яким можна нехтувати|обсяг| і не взаємодіють один з|із| одним на відстані. Вважається|лічиться|, що при зіткненні|співзіткненні| молекули ідеального газу поводяться, як абсолютно пружні кульки. На основі експериментів з|із| достатньо|досить| розрідженими газами були встановлені|установлені| прості закони, справедливі для ідеального газу. 1. Закон Бойля - Маріотта (для ізотермічного процесу ).
2. Закон Гей-Люссака (для изохорного| процесу).
3. Закон Гей-Люсса.ка (для изобарного| процесу).
За допомогою законів Бойля - Маріотта і Гей-Люссака легко знайти зв'язок між об'ємом|обсягом|, тиском|тисненням| і температурою для довільного рівноважного стану ідеального газу:
де V0 – об'єм|обсяг| одного моля газу R – універсальна газова стала, чисельно рівна роботі, що здійснюється|скоюється,чиниться| одним молем газу при ізобарному нагріванні його на один градус. Рівняння 4 називається рівнянням Менделєєва - Клапейрона. Для будь-якої маси газу воно запишеться|занотується| у вигляді:
де - число молей. Моль – кількість речовини системи, в якій міститься|утримується| стільки ж структурних елементів (молекул, атомів, іонів, електронів і ін. часток|часток,часточок|), скільки атомів міститься|утримується| в 0,012 кг нукліда С|із| (ізотопу вуглецю з|із| атомною масою 12). З|із| даного визначення, очевидно, що молі різних газів, містять|утримують| однакове число молекул, зване числом Авогадро NA = 6,023×1023 молекул/моль μ =m/v називається молярною масою газу. Маса моля, виражена|виказана,висловлена| в грамах, чисельно рівна відносній молекулярній масі. Лабораторна робота №2 Теоретична частина Теплоємністю речовини називають кількість теплоти, яка необхідна для нагрівання речовини на один градус. У теплотехнічних розрахунках використовують питому теплоємність, що описує процес нагрівання одиниці кількості речовини на один градус. Наприклад, кількість теплоти у загальному термодинамічному процесі визначається так:
де Сxm - середня питома теплоємність у довільному процесі, характеризує кількість теплоти, яка необхідна для нагрівання кількості речовини, щоб змінити температуру від t1 до t2. Звідси: Кількість речовини може бути виміряна в кг, м3 або молях. Теплоємність реальних речовин залежить від термодинамічного процесу підведення теплоти. У практичних розрахунках найчастіше використовують теплоємність з підведенням теплоти за умови сталого об'єму – ізохорна теплоємність (Сv), або за сталого тиску – ізобарна теплоємність (Ср). Види теплоємностей, їх розмірності та позначення наведені у табл.2.1
Таблиця 2.1 Класифікація теплоємностей
Рис. 2.1. Схема проточного калориметра для визначення теплоємності повітря. 1 - калориметр, 2 - електричний нагрівач, 3 - вентилятор, 4,5 – термометри. Порядок|лад| виконання роботи Визначення теплоємності повітря проводимо за допомогою проточного калориметра, основою якого є труба завдовжки 1600мм, а товщина стінки δ = 9мм. У калориметрі (1) розміщений електричний нагрівач (2), який виділяє тепло для нагрівання потоку повітря. Живлення нагрівача здійснюється від автотрансформатора, конструкція якого дозволяє регулювати потужність нагрівача. Вимірювання напруги U і струму у колі нагрівача здійснюється вольтметром та амперметром. Повітря за допомогою вентилятора пропускається через калориметр. Витрату повітря вимірюємо за допомогою трубки Прандтля. Температуру повітря на вході і виході калориметра t 1 і t2 вимірюється термометрами (4 ) і (5). Перед дослідом необхідно включити регулятор(3). Після чого включаємо нагрівач калориметра і регулюємо його потужність так, щоб температура повітря на виході з калориметра була більшою від його вхідної температури на 15-200С. Вимірювання температури на вході t1 і навиході t2 З калориметра, а також напруги і струму починаємо проводити після встановлення теплового режиму, тобто через 8-10 хвилин. Вимірювання величини робимо через кожні 3хв. Протягом 12хв. Дані вимірювань заносимо у табл.2.2. Таблиця 2.2 Результати вимірювань
За середніми значеннями величин (t1, t2, Δh, U, І) розраховуємо середню об’ємну теплоємність повітря для сталого тиску С'pm в інтервалі зміни температур від t1 до t2. Кількість теплоти, яка підведена до повітря за 1 с, визначається добутком сили струму на напругу. Об'ємну витрату V0 повітря через калориметр приведено до нормальних умов (Т0 = 273 К, Рн = 760 мм.рт.ст.): де Vt - об'ємна витрата повітря через калориметр, для температури повітря tп; F - площа поперечного перерізу труби; W - швидкість руху повітря; d - діаметр труби калориметра; Δ h – різниця тисків виміряна трубкою Піто, мм.вод.ст.; ρп – густина повітря кг/м3 . Знаючи об'ємну теплоємність для сталого тиску, можемо визначити середню масову теплоємність для Р = const у цьому ж інтервалі зміни температур де μ – молекулярна маса повітря, що дорівнює 28,97 кг/моль. Результати обчислення записати у табл. 2.3.
Таблиця 2.3 Результати обчислення
Контрольні питання
1. Що називається „ теплоємністю” та які є види теплоємності? 2. Що таке „масова”, „об'ємна” і „мольна” теплоємності? 3. У яких одиницях вимірюється теплоємність? 4. Як визначається істина і середня теплоємності? 5. Чому теплоємність за умови постійного тиску є завжди більшою від теплоємності для сталого об'єму? 6. Написати рівняння Майера і пояснити суть всіх величин у цьому рівнянні? 7. Як визначати середню теплоємність в інтервалі зміни температур від t1 до t2, користуючись таблицями теплоємностей від 0 до t0С? 8. Які є методи визначення теплоємностей? 9. Як визначається теплоємність проточним методом? 10. Як визначити масову теплоємність газової суміші? 11. Як визначити об'ємну теплоємність газової суміші? 12. Запишіть формулу для розрахунку внутрішньої енергії та ентальпії. 13. Як перерахувати масову теплоємність в об'ємну?
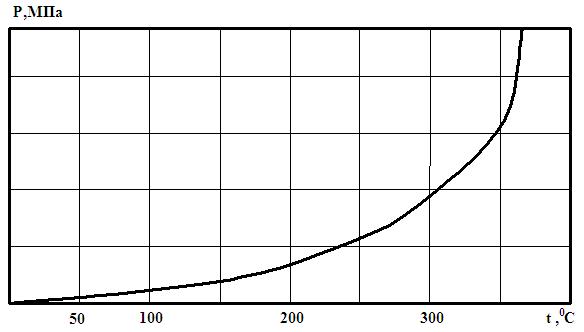
Лабораторна робота №4 Теоретична частина Експериментальним шляхом встановлено, що кожному значенню тиску відповідає певна температура кипіння рідини, яка є одночасно температурою насиченої пари, з підвищенням тиску збільшується температура кипіння рідини. У загальному вигляді зв'язок між тиском і температурою можна виразити рівнянням P = f (tn), де tn – температура насичення. Якщо побудувати у P – t системі координат (рис.3.1) залежність P = f (tn), то точки цієї кривої описують стан двофазної системи „вода – пар”. Діаграму P – t називають фазовою діаграмою.
Рис.3.1. Залежність P = f (tn)
Залежність тиску від температури для фаз, що знаходяться у рівноважному стані, описується рівнянням Клайперона – Клаузіуса:
де – r - прихована теплота пароутворення, кДж/кг; v" – питомий об'єм сухої насиченої пари, м3/кг; v' – питомий об'єм рідини у процесі кипіння, м3/кг. Величина прихованої теплоти пароутворення характеризує кількість теплоти, яку необхідно затратити, щоб перетворити 1 кг рідини у процесі кипіння в суху насичену пару за умови сталого тиску. Волога насичена пара складається з сухої насиченої пари і краплинок киплячої рідини. Вона характеризується тиском Р або температурою tн і ступінню сухості x. Ступінь сухості – це відношення маси сухої насиченої пари mс.п., що міститься у вологій насиченій парі, до маси вологої пари mв.п:
Є наступні методи визначення ступеня сухості пари: а) метод конденсації – полягає у тому, що волога насичена пара, ступінь сухості якої визначать, подається уводу і вона конденсується. Знаючи масу води m1 і температуру t1 до конденсації пари, масу води m2 і температуру t2 після конденсації, а також тиск пари, можна визначити ступінь сухості за співвідношенням:
де mн – маса конденсованої пари, кг; mв – маса води в термостаті, кг; Св – теплоємність води, кДж/(кг∙К); t1 і t2 – температура води до і після конденсації пари, 0С; i - ентальпія киплячої води для даного тиску, кДж/кг; i2 – ентальпія води після конденсації пари, кДж/кг; б) сепараційний метод – виділення краплинок води з вологої насиченої пари під діею відцентрових сил. в) електричний метод (ємнісний) – порівняно діелектричної проникливості води (εв = 80) і сухої насиченої пари (εп = 1). г) дросельний метод полягає утому, що відбірна проба вологої насиченої пари направляється у дросельний калориметр, у якому після дроселювання переходить у стан перегрітої водяної пари. Знаючи тиск Р2 і температуру t2 пари після дроселювання, а також тиск вологої насиченої пари Р і вважаючи початкові і кінцеві ентальпія (i 1= i 2), за i- S діаграмою знаходять ступінь сухості пари x. Порядок|лад| виконання роботи Під час проведення лабораторної роботи необхідно виконати два завдання, а саме: Встановити залежності між тиском і температурою насиченої водяної пари і визначити ступінь сухості вологої насиченої пари. Завдання 1.Встановлення залежності між тиском і температурою насиченої водяної пари статичним методом Установку для встановлення залежності між тиском і температурою насиченої водяної пари показано на рис2.3.
Рис.3.2.Схема установки для встановлення залежності P = f (tn). 1 – калориметр; 2 – електричний нагрівач; 3 – манометр; 4 – штуцер; 5 -термопара. Вона складається з товстостінної посудини (1), ззовні котрої намотаний електричний нагрівач (2). До посудини приєднаний манометр (3), а у штуцер (4) встановлена термопара (5), яка приєднана до потенціометра (6). Посудина (1) наповнена водою так, щоб питомий об'єм води був критичним vкр. Після ознайомлення з установкою необхідно включити електричний нагрівач та стежити за зміною тиску і температури у посудині. Коли тиск досягне 0,1 МПа починаємо заміряти його значення через 0,2 МПа і одночасно її температуру. Виміри робимо до величини вказаної керівником. Результати вимірювань заносимо у табл.3.1. Таблиця 3.1
Результати вимірювань
За цими результатами будуємо в P-t системі координат криву залежності P = f (tn). Приховану теплоту пароутворення r величини v' і v" знаходимо за таблицями насиченої пари, а значення похідних dp і dT знаходимо за допомогою графіку P = f (tn). Розрахунки заносимо у табл. 3.2.
Таблиця 3.2. Результати обчислення
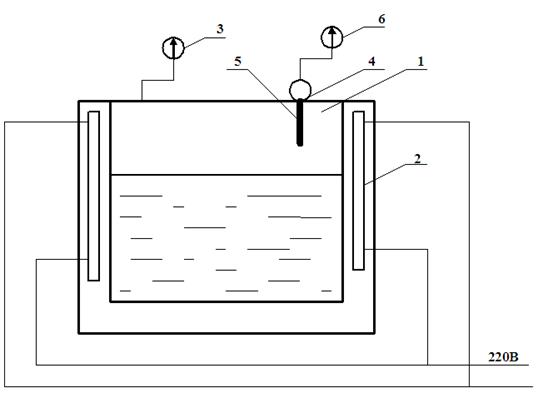
Завдання 2.Визначення ступеня сухості вологої насиченої пари методом конденсації Установку для визначення ступеня сухості насиченої водяної пари показано на рис.3.3. Вона складається з парогенератора (1) з електричним нагрівником (2), термостата (3), заповненого водою, манометра (4) для вимірювання тиску водяної пари, термометра (5) для вимірювання температури води у термостаті та крана (6).
Рис.3.3. Схема установки для визначення ступеня Лабораторна робота №5 ВИЗНАЧЕННЯ ВІДНОШЕННЯ|ставлення| ТЕПЛОЕМКОСТЕЙ| ГАЗУ ЗА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА| Мета роботи: Метою|ціллю||теперішньої,даної| роботи є|з'являється,являється| вивчення процесів, що відбуваються|походять| в газі при вимірюванні|вимірі| відношення|ставлення| питомих теплоємностей| Теоретична частина Питомою теплоємністю газуназивається кількість тепла, необхідне для нагрівання одиниці маси газу на один градус. Величина теплоємності газів залежить від умов їх нагрівання. Запишемо перший початок термодинаміки:
де dQ – кількість тепла, що підводиться до термодинамічної системи і витрачається на збільшення її внутрішньої енергії dU і на роботу dA, що здійснюється|скоюється,чиниться| системою проти|супроти| зовнішніх сил. За визначенням теплоємності
де елементарна робота dA = pdV
Розглянемо|розгледимо| два випадки: 1. Газ нагрівається при незмінному об'ємі|обсязі| V = const. В цьому випадку dV = 0 і робота зовнішніх сил рівна нулю dA = pdV = 0, отже, все передане газу ззовні тепло йде на збільшення його внутрішньої енергії dU. Тоді з|із| рівняння (2) виходить, що теплоємність при постійному об'ємі|обсязі| рівна:
2. Газ нагрівається при постійному тиску|тисненні| p = const. В цьому випадку отримане|отримуване| газом ззовні тепло йде не тільки|не лише| на збільшення його внутрішньої енергії dU, але і на здійснення газом роботи dA проти|супроти| зовнішньої сили тиску|тиснення|. Тоді теплоємність при постійному тиску|тисненні| рівна:
Отже, для нагрівання одиниці маси газу на один градус при p = const буде потрібно більше тепла, ніж при V = const. Знайдемо зв'язок між Ср і Сv. Скориставшись рівнянням стану ідеального газу для одиниці маси ідеального газу, отримаємо|отримаємо|:
При p = const, dp = 0, і тоді
Підставивши цей вираз в (4) і замінивши dU/dT на Cv згідно (3) (для одиниці маси), отримаємо|отримаємо|:
Таким чином, питома теплоємність Ср більше питомої теплоємності Сv на величину R/μ, яка є роботою, що здійснюється|скоюється,чиниться| одиницею маси газу при розширенні, що відбувається|походить| при постійному тиску|тисненні| в результаті|унаслідок,внаслідок| підвищення його температури на один градус. Разом з|поряд з,поряд із| питомою теплоємністю с|із|, часто користуються молярною теплоємністю C (теплоємність одного кіломоля речовини). Між ними є|наявний| очевидне співвідношення
Тоді співвідношення ( 6 ) можна записати у вигляді|виді|:
Згідно закону рівнорозподілення| енергії за ступенями вільностіна кожну ступінь вільності молекули ідеального газу доводиться|припадає,приходиться| в середньому однакова енергія, рівна 1/2kT (k – постійна Больцмана). Тому внутрішню енергію одного кіломоля ідеального газу можна знайти за формулою:
де NА – число Авогадро, i – число ступенів вільності молекули газу. Підставивши цей вираз в (3), отримаємо|отримаємо|:
Число ступенів вільності визначається числом атомів в молекулі і характером|вдачею| зв'язку між ними. Для одноатомного газу i = 3; для двоатомного – i = 5 (жорсткий зв'язок), i = 6 (пружний зв'язок); для трьох і більш атомів в молекулі i = 6 (жорсткий зв'язок, нелінійна молекула). Оскільки|тому що|
то
і
Величини cp і cv можна визначити експериментально. Проте|однак| існує спосіб безпосереднього визначення відношення|ставлення| cp/cv = γ яке залежить тільки|лише| від числа ступенів вільності молекул газу. Це відношення|ставлення| входить у вираз|вираження| закону Пуассона, що описує адіабатичний процес в газах.
Адіабатичним процесомназивається процес, що протікає без теплообміну з|із| навколишнім середовищем. Такий процес відбуватиметься|походитиме| в системі, оточеній абсолютно|цілком| нетеплопровідними стінками. Оскільки|тому що| абсолютно|цілком| нетеплопровідних стінок не буває, реально процес може лише наближатися до адіабатичного. Якщо процес протікає достатньо|досить| швидко, так що система не встигає|устигає| вступити в теплообмін з|із| навколишнім середовищем, то його можна рахувати практично адіабатичним і за відсутності хорошої|доброї| теплової ізоляції (наприклад, при швидкому стисненні|стискуванні| або розширенні газу). Перший початок термодинаміки для адіабатичного процесу приймає вигляд|вид|:
тобто|цебто| при адіабатичному розширенні робота здійснюється|скоюється,чиниться| газом тільки|лише| в результаті|унаслідок,внаслідок| зміни запасу його внутрішньої енергії. Адіабатичне розширення супроводжується|супроводиться| пониженням температури, а адіабатичне стиснення|стискування| – підвищенням температури. Виведемо рівняння адіабатичного процесу (рівняння Пуассона). Оскільки dA = pdV, то, використавши вираз|вираження| (8), знайдемо
Поділивши рівняння (5) на (9) і взявши до уваги, отримаємо|отримаємо|
звідки
де
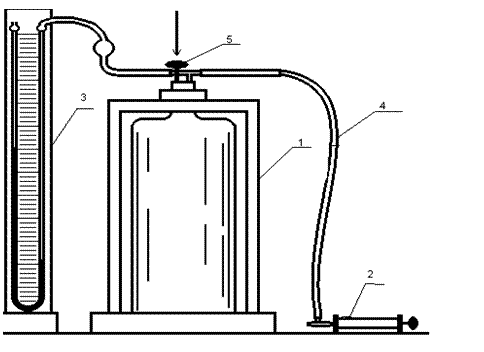
Після|потім| інтеграції і потенціювання (10) одержимо|отримаємо| рівняння Пуассона PV2 = const Прилад Клемана-Дезорма, за допомогою якого можна визначити величину ср/сv (рис4.1). Він є балоном (1) на 10 л з|із| повітрям, яке накачується ручним насосом (2) до деякого тиску|тиснення| p, надлишок якого h = p – p0 над атмосферним p0 визначається по водяному манометру (3), який сполучається з балоном (1) гумовим шлангом (4). Для здійснення швидкого (адиабатного|) розширення повітря з|із| балона (1) до атмосфери служить клапан (5).
Рис.4.1.Схема установки Клемона – Дезорма для визначення відношення теплоємностей газу 1- балон; 2 – ручний насос; 3 - водяний манометр; 4 – гумовий шланг; 5 – клапан. Виділимо (у думках) усередині повітря, що знаходиться|перебуває| в балоні (1), деяку масу m і простежимо за зміною її стану під час експерименту|досліду| при одночасній зміні тиску|тиснення| p і температури T. Якщо клапан (5) відкритий|відчинений|, то тиск|тиснення| в судині|посудині| рівний атмосферному P0; температура повітря в судині|посудині| рівна T0 – температурі навколишнього середовища. Тоді параметрами виділеної в думках маси повітря будуть, V0, T0, P0 де V0 – об'єм|обсяг| даної маси повітря при тиску|тисненні| P0 і температурі T0. Якщо тепер закрити|зачинити| клапан (5) і накачати за допомогою насоса в судину|посудину| деяку кількість повітря, то маса повітря, що розглядається|розглядується| нами, стиснеться|стискуватиметься|, а температура і тиск|тиснення| її підвищаться. Через деякий час у наслідок|внаслідок| теплообміну з|із| навколишнім середовищем температура повітря в судині|посудині| стане рівною T0. Тиск|тиснення| же буде рівний:
де h1 – остаточна (після|потім| встановлення теплової рівноваги з|із| навколишнім середовищем) різниця рівнів рідини в манометрі. Стан даної маси повітря визначається тепер параметрами V1 , P1, T0 – це I стан виділеної маси повітря; V1 – об'єм|обсяг| даної маси повітря при тиску|тисненні| P1 і температурі T0. Якщо на короткий час (~ 1-2 с|із|) відкрити|відчинити| клапан (5), то повітря, що знаходиться|перебуває| в балоні, швидко (за адіабатою) розшириться і внаслідок цього охолоджується. В кінці|у кінці,наприкінці| цього малого проміжку часу, протягом якого клапан (5) відкритий|відчинений|, і балон сполучається з атмосферою, тиск|тиснення| повітря у середині судини|посудини| стане рівним тиску|тисненню| атмосфери, і стан даної маси повітря визначатиметься у цей момент наступними|такими| параметрами, V2, P0, T1 – це II стан виділеної маси повітря; V2 – об'єм|обсяг| даної маси повітря при тиску|тисненні| P0 і температурі T1. При цьому Коли тиск|тиснення| в судині|посудині| (1) стане|чинитиметься| рівним тиску|тисненню| атмосфери P0 (через 1-2 с|із|), клапан (5) закривають|зачиняють|. Повітря, що знаходиться|перебуває| в балоні (1), починає|розпочинає,зачинає| нагріватися від T1 до T0 у наслідок|внаслідок| отримання|здобуття| тепла від навколишнього середовища, тиск|тиснення| в судині|посудині| починає|розпочинає,зачинає| підвищуватися і стане рівним:
де h2 – різниця рівнів рідини в манометрі після того, як температура газу в балоні стане рівній температурі навколишнього середовища. Дана маса повітря тепер характеризується параметрами V2, P2, T0 – це III стан даної маси повітря. Отже, дана маса повітря під час експерименту знаходилася|перебувала| послідовно в трьох станах:
Перехід із стану I в стан II відбувається адіабатно, із стану II в – стан III – ізохорно.
Рис.4.2.Графіки процесів. На Рис4.2. зображені|змальовані| графіки процесів: крива I-II – адіабата, крива II-III – ізохора, крива III-I – ізотерма. Газ в станах I-III має однакову температуру. Перехід із|із| стану I в стан II описується рівнянням Пуассона:
Параметри станів I і III задовольняють закону Бойля-Маріотта:
Піднісши рівняння (15) до ступеня g і розділивши його за членами| на (14), отримаємо|отримаємо|:
Звідси
Враховуючи рівність (12) і (13), отримаємо|отримуємо|, що
і, підставляючи їх в рівність (16), маємо
Оскільки|тому що|
Прирівнявши праві частини|частки| (17) і (18), отримаємо|отримаємо| наступну|слідуючу| формулу:
яка і використовується в цій роботі для експериментального визначення g. Порядок|лад| виконання роботи
1. При закритому|зачиненому| клапані (5) ручним насосом (2) обережно накачують повітря в балон (1) до різниці рівнів рідини в манометрі 30 ¸ 35 см. 2. Вичікують 2 ¸ 3 хвилини, поки|доки| рівні рідини в манометрі не перестануть змінюватися; потім розраховують їх різницю h1 з точністю до|із точністю до| 1 мм. 3. Натискаючи|натискуючи| рукою на клапан (5), відкривають|відчиняють| його; при цьому чується шипіння повітря, що виходить з|із| балона (1). Клапан (5), залишається відкритим|відчиненим| протягом 1 ¸ 2 секунд, поки|доки| не припиниться шипіння повітря, що виходить з|із| балона (1), після чого клапан (5) закривають|зачиняють|. 4. Вичікують 2 ¸3 хвилини, стежачи за зміною рівнів рідини в манометрі; коли рівні встановляться, розраховують їх різницю h2 з точністю до|із точністю до| 1 мм. 5. Опит|дослід| проробляють 10 разів. Результати вимірювань|вимірів| записують|занотовують| в табл. 4.1. Таблиця 4.1. Лабораторна робота №1 ВИЗНАЧЕННЯ УНІВЕРСАЛЬНОЇ ГАЗОВОЇ СТАЛОЇ МЕТОДОМ ВІДКАЧУВАННЯ Мета|ціль| роботи: визначити універсальну газову сталу. Обладнання: вакуумний насос, мановакуумметр|, барометр, термометр скляна куля, ваги з|із| важками. Теоретична частина Для вивчення фізичних властивостей макроскопічних систем, що складаються з великого числа часток|часток,часточок|, використовують два методи – статистичний і термодинамічний. Статистичний метод заснований на законах теорії вірогідності|ймовірності| і математичної статистики. Розділ теоретичної фізики, в якій вивчають фізичні властивості макроскопічних систем за допомогою статистичного методу, називається статистичною фізикою. Термодинамічний метод полягає у вивченні фізичних властивостей макроскопічних систем шляхом
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.160.29 (0.016 с.) |

 ,
,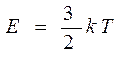
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) ,
,
 а
а



 ,
,  ,
, ,
,

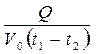

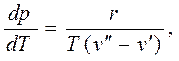
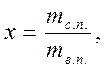

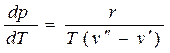

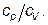

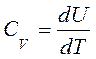 .
.
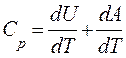 .
.
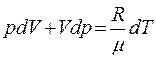
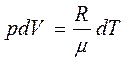
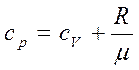
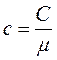

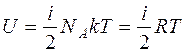 ,
,
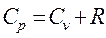 або
або 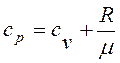
 або
або 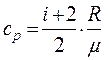

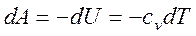
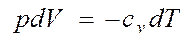 .
.
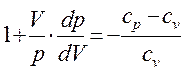
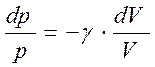

 ,
,
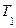 <
<  .
. ,
,
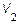 ,
,

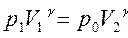
 .
.
 ,
,
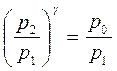 ,
,
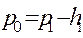 ,
,
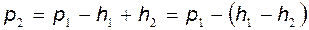

 .
.