
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движущая сила массообменных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Движущей силой массообменных процессов является разность концентраций (градиент концентраций) фактической в данной фазе G и равновесной с фактической в другой фазе L. Процесс протекает в направлении той фазы, в которой концентрация компонента меньше, чем это следует из условия равновесия.
Движущая сила может быть выражена в любых единицах концентраций, но всегда Движущая сила пропорциональна скорости массообменного процесса. Она может быть средней интегральной и средней логарифмической. Движущая сила зависит от положения рабочей и равновесной линий, чем ближе линии друг к другу, тем она меньше.
Движущую силу и кинетику выражают тремя способами:
Средняя интегральная движущая сила Средняя движущая сила определяет количество переданной массы вещества. Т.к рабочие и равновесные концентрации изменяются вдоль поверхности контакта фаз, то нужно рассчитывать среднюю движущую силу процесса. Допустим что рабочая и равновесная линия – кривые или раб.линия–прямая, а равн.линия –кривая.
Дифференциальное уравнение материального баланса:
Дифференциальное уравнение массопередачи:
Средняя логарифмическая движущая сила частный случай: линия равновесия – прямая
Число единиц переноса (ЧЕП)
ЧЕП показывает, сколько единиц вещества переходит в другую фазу при величине движущей силы, равной единице
Теоретическая тарелка, ВЭТТ
1) Теоретическая тарелка – контактное устройство, обеспечивающее получение равновесных потоков фаз, покидающих контактную зону. Одна ТТ – одно изменение концентраций по жидкой фазе и одно изменение по паровой фазе. ТТ используют при расчетах массообменных аппаратов, когда нужно учитывать время контакта фаз, необходимое для достижения равновесия. Преимуществом метода ТТ является то, что нужно иметь только уравнение равновесия и уравнение рабочей линий. Вместо понятия ТТ используют ЧТТ. ЧТТ зависит от взаимного расположения рабочей и равновесной линии 2)
объединяя урав (1) и (2), интегрируем →
где H, S –высота и сечение ап/та, G –расход ф.G [кг/с],
из урав (5) →
Правило фаз ГИББСА Равновесной системой называется такая система, которая может существовать неограниченно долго без каких-либо качественных или количественных изменений. Состояние равновесия характеризуется правилом фаз Гиббса, которое определяет связь между числом степеней свободы, числом ее компонентов и числом фаз. Число независимых параметров, которые могут быть выбраны произвольно, чтобы привести систему в состояние равновесия – число степеней свободы.
В качестве степеней свободы могут выступать t,P,c Для 2-х компонентной системы взаимно растворимых жидкостей L=2, а для нерастворимых L=1 Вывод уравнения: 1) Пусть система содержит N фаз и n компонентов в каждой фазе. 2) Состояние фаз фиксировано при Р и Т. 3) Состав каждой фазы можно рассчитать, задавая n-1 концентраций компонентов, а концентрация одного из компонентов является зависимой величиной и может быть рассчитана из условия, что сумма мольных долей всех компонентов в смеси равна 1. 4) 5) 6) Число уравнений не может превышать числа переменных, иначе уравнения будут несовместимыми. Разность между числом независимых переменных и числом уравнений равна числу произвольно изменяемых параметров в данной системе, меняя которые можно не менять число фаз в ней (степень свободы):
ПРИМЕНЕНИЕ ПРАВИЛА ФАЗ К ПРОЦЕССАМ ПЕРЕГОНКИ Компонентами системы называются те составные части, концентрация которых может претерпевать изменения в различных фазах. Состояние равновесия подчиняется правилу фаз Гиббса: L = n + 2 – N
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.007 с.) |

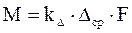 - основное уравнение массопередачи → средняя движущая сила процесса определяет количество переданной массы вещества.
- основное уравнение массопередачи → средняя движущая сила процесса определяет количество переданной массы вещества. где с – рабочая концентрация компонента в одной фазе,
где с – рабочая концентрация компонента в одной фазе, 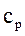 - концентрация компонента для данной фазы, равновесная с рабочей концентрацией в другой фазе.
- концентрация компонента для данной фазы, равновесная с рабочей концентрацией в другой фазе.
 ,
,  разность концентраций
разность концентраций
 ,
, 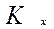 коэффициент массопередачи
коэффициент массопередачи
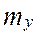 ,
,  число единиц переноса (ЧЕП)
число единиц переноса (ЧЕП)
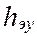 ,
, 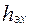 высота, эквивалентная единице переноса (ВЕП)
высота, эквивалентная единице переноса (ВЕП)
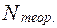 число теоретических тарелок
число теоретических тарелок
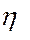 или
или  К.п.д или высота, эквивалентная теоретической тарелке (ВЭТТ)
К.п.д или высота, эквивалентная теоретической тарелке (ВЭТТ)



 ;
; 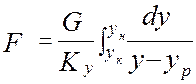
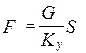

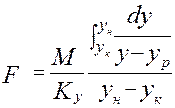
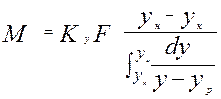

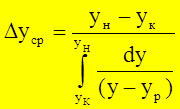 - средняя интегральная разность концентраций для газ. фазы
- средняя интегральная разность концентраций для газ. фазы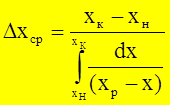 - средняя интегральная разность концентраций для жид. ф
- средняя интегральная разность концентраций для жид. ф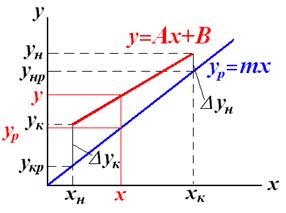
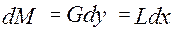 ;
;  ;
; 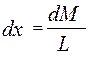
 ;
;  ;
; 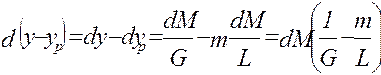
 ;
; 

 ;
;  ;
; 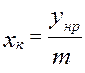 ;
; 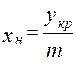
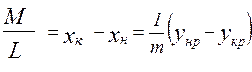 ;
; 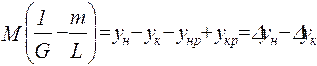
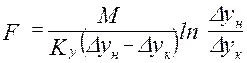
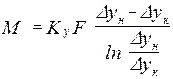

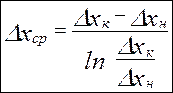


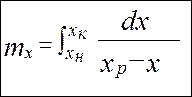
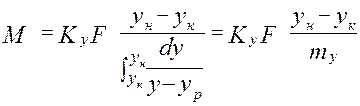
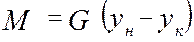 ;
; 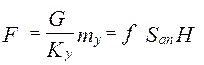
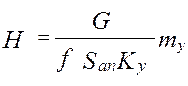 ;
; 
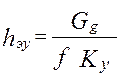 ;
; 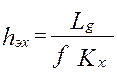 ;
; 
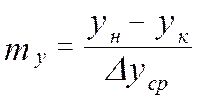
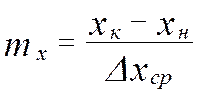
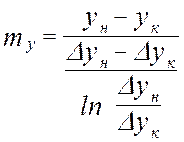
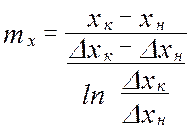
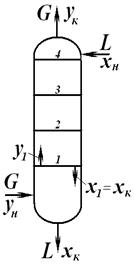

 от величины движущей силы процесса. При сближении рабочей и равновесной линии ∆ ↓ → ЧТТ ↑ и наоборот. ЧТТ используется для определения высоты контактной зоны аппарата Н, для этого используют ВЭТТ.
от величины движущей силы процесса. При сближении рабочей и равновесной линии ∆ ↓ → ЧТТ ↑ и наоборот. ЧТТ используется для определения высоты контактной зоны аппарата Н, для этого используют ВЭТТ. (1) – мат.баланс фазы G в интегральной форме
(1) – мат.баланс фазы G в интегральной форме (2) – уравнение массопередачи
(2) – уравнение массопередачи (3) - поверхность фазового контакта
(3) - поверхность фазового контакта (4) – поверхность массообмена для насадочных аппаратов, где
(4) – поверхность массообмена для насадочных аппаратов, где - раб.V аппарата*поверхность контакта фаз в 1 его V.
- раб.V аппарата*поверхность контакта фаз в 1 его V.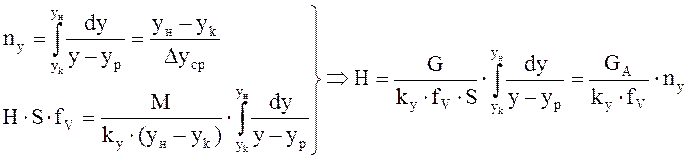 (5) – высота аппарата,
(5) – высота аппарата, -массовая скорость ф.G [
-массовая скорость ф.G [ 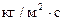 ]
] - высота, эквивалентная одной единице переноса.
- высота, эквивалентная одной единице переноса. где L – число степеней свободы n – число компонентов N – число фаз
где L – число степеней свободы n – число компонентов N – число фаз
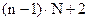 - общее число переменных, определяющих состояние системы.
- общее число переменных, определяющих состояние системы.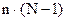 - общее число уравнений для расчета состояния системы, где (N-1) – число уравнений, достаточных для расчета концентрации компонентов, n – число переменных.
- общее число уравнений для расчета состояния системы, где (N-1) – число уравнений, достаточных для расчета концентрации компонентов, n – число переменных.



