
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие идеальных бинарных смесей, изотерма паровой и жидкой фазыСодержание книги
Поиск на нашем сайте Рассмотрим случай, когда бинарная смесь образует идеальный раствор, подчиняющийся законам Рауля и Дальтона. Состояние такой системы характеризуется π, t, По закону Рауля парциальные давления определяются: для НКК - для ВКК - Общее давление насыщенных паров смеси равно сумме парциальных давлений компонентов:
Так как жидкость находиться в равновесии с соответствующим нас.паром (t кип) → состав жидкой фазы - По закону Дальтона парциальное давление в паровой фазе определяется: для НКК - для ВКК - При равновесии парциальные давления каждого компонента в паровой и жидкой фазах равны:
из урав (1) и (1а) определяем состав паровой фазы, находящейся в равновесии с жидкостью состава:
из урав (2) →
При использовании закона Генри: уравнение изотермы жидкой фазы - уравнение изотермы паровой фазы -
20. Графический метод расчета равновесных составов фаз
Состав жидкой и паровой фаз можно определить по известным кривым зависимости давления насыщенных паров от температуры. В точках M и N пересекаются линии заданного внешнего давления π и кривые давления насыщенных паров. В этих точках определяются температуры кипения чистого НКК ( При выбранной t, давление нас.паров НКК – т.L, давление нас.паров ВКК – т.K. Отложив эти значения на правом графике в т.А и в т.В, проводим через них изотерму ВА. т.D – определяет состав кипящей жидкости ОА – закон Рауля, выражает зависимость между составом жидкой фазы и парциальным давлением НКК. т.Е – парциальное давление НКК при найденном значении ОН – закон Дальтона, выражает зависимость между составом жидкой фазы и парциальным давлением НКК. Условие равновесия
Кривая равновесия фаз
По закону Рауля парциальные давления в жидкой фазе определяются: для НКК - для ВКК - По закону Дальтона парциальное давление в паровой фазе определяется: для НКК - для ВКК - При равновесии парциальные давления каждого компонента в паровой и жидкой фазах равны:
разделим урав (1) на (2) →
Уравнение устанавливает зависимость между равновесными концентрациями в жидкой и паровой фазах. Каждой точке на КРФ соответствует определенная температура в пределах температур кипения НКК (
Изобарные температурные кривые
Полученные при разных t равновесные составы жидкой Изобарно-температурные кривые позволяют установить связь между Т кипения системы и составом жидкой и паровой фаз.
B 2 точка А -
пар 1 - линия кипения. пар + 2 – линия конденсации. S S’ SS’- конода, линия соединяющая точки равновесных жидкость составов жидкой и паровой фаз.
1 A жидкая фаза
Энтальпийная (тепловая) диаграмма
Энтальпийная диаграмма связывает составы жидкой и паровой фаз с их энтальпиями. Их используют при расчетах ректификации, когда нужно знать тепловые потоки
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.005 с.) |

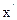 ,
,  . L=2 (произвольно определяем 2 параметра).
. L=2 (произвольно определяем 2 параметра).

 - уравнение изотермы жидкой фазы, выражает зависимость между составом жидкой и паровой фазы и давлением насыщенных паров этой жидкости
- уравнение изотермы жидкой фазы, выражает зависимость между составом жидкой и паровой фазы и давлением насыщенных паров этой жидкости →
→


 =
= 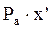 (1)
(1) =
=  (1a)
(1a) (2)
(2) - уравнение изотермы паровой фазы.
- уравнение изотермы паровой фазы. используется для определения температуры кипения смеси при давлении π.
используется для определения температуры кипения смеси при давлении π.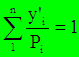 используется для определения температуры начала конденсации паровой фазы при π.
используется для определения температуры начала конденсации паровой фазы при π.

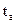 ) и ВКК (
) и ВКК ( ).
). =
=  → т.F – концентрация НКК в паровой фазе.
→ т.F – концентрация НКК в паровой фазе.

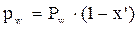


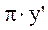 =
=  =
=  (2)
(2)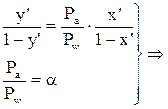 (3)
(3) - уравнение кривой равновесия фаз.
- уравнение кривой равновесия фаз.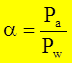 - коэффициент относительной летучести. Характеризует способность компонента переходить в паровую фазу. Чем он больше, тем легче компонент переходит. КОЛ зависит от температуры и давления, зависимость обратнопропорциональная.
- коэффициент относительной летучести. Характеризует способность компонента переходить в паровую фазу. Чем он больше, тем легче компонент переходит. КОЛ зависит от температуры и давления, зависимость обратнопропорциональная.  >1.
>1.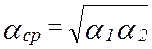


 относительное количество паров
относительное количество паров относительное количество жидкости
относительное количество жидкости T
T =
=  =1 – температура кипения НКК (
=1 – температура кипения НКК ( =
= 


 энтальпия НКК в жидкой фазе.
энтальпия НКК в жидкой фазе. - энтальпия ВКК в паровой фазе.
- энтальпия ВКК в паровой фазе. - энтальпия ВКК в жидкой фазе.
- энтальпия ВКК в жидкой фазе. - энтальпия НКК в паровой фазе.
- энтальпия НКК в паровой фазе.


