Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые ряды. Общий член ряда. Сумма ряда. Сходимость ряда. Cвойства сходящихся рядов. Остаток ряда.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РЯДЫ. Числовые ряды. Общий член ряда. Сумма ряда. Сходимость ряда. Cвойства сходящихся рядов. Остаток ряда. u1;u2;…un… - бесконечная последовательность чисел u. Sn=u1+u2…+un - n-ая сумма последовательности.
u1;u2 – члены ряда; un – общий член; тогда Sn можно назвать n-ой частичной суммой ряда.
1) Док-во.
3) если к ряду (1) прибавить (или отбросить конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно. Также следует, если ряд (1) сходится, то его остаток Rn=S – Sn = un+1+un+2+… стремится к нулю при n–>∞, т.е. Необходимый признак сходимости. Гармонический ряд.
Знакоположительные числовые ряды. Признак сравнения (две формы). 1. Даны два знакоположительных ряда: Если " an≥bn, то а) б) Доказательство. Пусть
ограничен сверху S. Кроме того последовательность SN ↑, т.к. SN+1=SN+bn+1 и SN+1 - SN= bn+1≥0 1) Un ↑ и ограничено сверху => $ limSn=S, т.о. 2) от противного: если an сходится, то найдется и bn, что противоречит условию=> an расх. 2. Признак сравнения в предельной форме.
Док-во. Пусть
Знакоположительные числовые ряды. Признак Даламбера. Признак Даламбера:
Доказательство.
Знакоположительные числовые ряды. Радикальный признак Коши.
Док-во. Пусть $
Таким образом получаем: Знакоположительные числовые ряды. Интегральный признак Коши.
суммируем то, что получилось:
Если интеграл сходится, то сходится и меньший ряд Если интеграл расходится, то расходится и больший ряд Исследование ряда Дирихле. Следствие. Ряд Дирихле:
Знакопеременные ряды. Абсолютная и условная сходимость. Теорема сходимости знакопеременного ряда.
ряд Теорема. Если Доказательство. Пусть S+ - сумма положительных элементов, S- - сумма отрицательных элементов (по модулю). Тогда Sn= S++ S-= Эти послед-ти имеют пределы. S+ и S- - сходятся.
Обратное неверно. Определение. Если Признак Лейбница сходимости знакочередующегося числового ряда. Схема исследования на абсолютную и словную сходимость.
Док-во. a1-a2+a3-a4+a5-a6+… сгруппируем члены попарно:
с другой стороны: a1-a2+a3-a4+a5-a6+…=a1-(a2-a3)-(a4-a5)-…<a1, т.е. сумма ряда ограничена. V1= a2-a3>0; V2= a4-a5>0; S2n=U1+U2…+Un ↑= a1-V1-V2…-Vn-a2n<a1 ↑ и ограничена последовательностью S2n имеет предел S.
Определение. Если Схема исследования:а) проверяем Функциональные ряд, область сходимости.
совокупность точек сходимости ряда называется областью сходимости ряда. Как правило, по Даламберу.
Степенной ряд. Теорема Абеля. Радиус и интервал сходимости.
от (1) к (2) легко перейти, сделав замену t=x - x0 Теорема Абеля. а) если x1 – точка сходимости ряда (2), то " x: |x|<|x1| - ряд сходится.
б) если x2 – точка расходимости ряда (2), то " x: |x|>|x2| - ряд расходится.
Свойства степенных рядов. Почленное дифференцирование и интегрирование степенного ряда.
Формула Эйлера.
выделим действительную и мнимую части
38. Разложение в ряд Маклорена функций
39. Разложение в ряд Маклорена логарифмических функций: y=ln(1+x), y=ln(1-x), y=ln
40. Разложение в ряд Маклорена биномиальной функции f(x)=(1+x)m, где m- произвольное действительное число.
41. Разложение в ряд Маклорена обратных тригонометрических функций: y=arctgx; y=arcsinx.
РЯДЫ. Числовые ряды. Общий член ряда. Сумма ряда. Сходимость ряда. Cвойства сходящихся рядов. Остаток ряда. u1;u2;…un… - бесконечная последовательность чисел u. Sn=u1+u2…+un - n-ая сумма последовательности.
u1;u2 – члены ряда; un – общий член; тогда Sn можно назвать n-ой частичной суммой ряда.
1) Док-во.
3) если к ряду (1) прибавить (или отбросить конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно. Также следует, если ряд (1) сходится, то его остаток Rn=S – Sn = un+1+un+2+… стремится к нулю при n–>∞, т.е.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.211.135 (0.007 с.) |



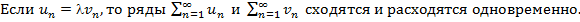









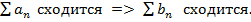

 сходится и
сходится и  , тогда
, тогда  , т.к.
, т.к.


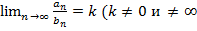 т.е. " e $ N: при a≥N
т.е. " e $ N: при a≥N  . Выберем e и возьмем N:
. Выберем e и возьмем N:  Просуммируем.
Просуммируем. Если
Если  сход => меньший ряд тоже сход.=>
сход => меньший ряд тоже сход.=>  сход.=>
сход.=>  сход. Обратное (расх.) аналогично.
сход. Обратное (расх.) аналогично.




 , т.е. " e $ N, "n≥N;
, т.е. " e $ N, "n≥N;  ; выберем e<q и раскроем модуль.
; выберем e<q и раскроем модуль.  => просуммируем
=> просуммируем , тогда 1) q<1 выберем e так, что q+e<1, тогда правый сход, как геометрический и
, тогда 1) q<1 выберем e так, что q+e<1, тогда правый сход, как геометрический и 


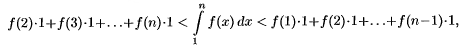


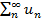 => сходится и исходный ряд.
=> сходится и исходный ряд.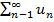 .
.

 - числовой ряд, содержащий бесконечное число положительных и бесконечное число отрицательных рядов, называется знакопеременным.
- числовой ряд, содержащий бесконечное число положительных и бесконечное число отрицательных рядов, называется знакопеременным.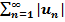
 сход =>
сход => 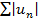 существует. S+ и S- возрастают соответственно, причем S+≤ Sn и S- ≤Sn, т. о. последовательности S+ и S- и ограничены Sn
существует. S+ и S- возрастают соответственно, причем S+≤ Sn и S- ≤Sn, т. о. последовательности S+ и S- и ограничены Sn - разность сходящихся рядов сходится.
- разность сходящихся рядов сходится. сходится, если: а) |an|¯; б)
сходится, если: а) |an|¯; б) 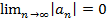


 сход, а
сход, а  расх., такая сходимость называется условной.
расх., такая сходимость называется условной.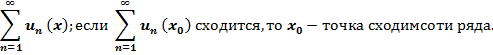










 и
и  .
.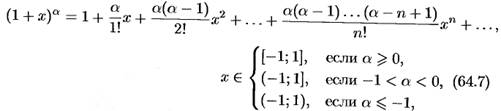
 , предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
, предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
 тогда
тогда
 .
.

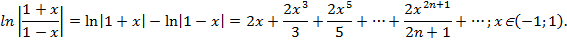


 , предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
, предполагая, что в формуле (64.7) a= - 1; x=-x, тогда