Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак сходимости. Гармонический ряд.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знакоположительные числовые ряды. Признак сравнения (две формы). 1. Даны два знакоположительных ряда: Если " an≥bn, то а) б) Доказательство. Пусть
ограничен сверху S. Кроме того последовательность SN ↑, т.к. SN+1=SN+bn+1 и SN+1 - SN= bn+1≥0 1) Un ↑ и ограничено сверху => $ limSn=S, т.о. 2) от противного: если an сходится, то найдется и bn, что противоречит условию=> an расх. 2. Признак сравнения в предельной форме.
Док-во. Пусть
Знакоположительные числовые ряды. Признак Даламбера. Признак Даламбера:
Доказательство.
Знакоположительные числовые ряды. Радикальный признак Коши.
Док-во. Пусть $
Таким образом получаем: Знакоположительные числовые ряды. Интегральный признак Коши.
суммируем то, что получилось:
Если интеграл сходится, то сходится и меньший ряд Если интеграл расходится, то расходится и больший ряд Исследование ряда Дирихле. Следствие. Ряд Дирихле:
Знакопеременные ряды. Абсолютная и условная сходимость. Теорема сходимости знакопеременного ряда.
ряд Теорема. Если Доказательство. Пусть S+ - сумма положительных элементов, S- - сумма отрицательных элементов (по модулю). Тогда Sn= S++ S-= Эти послед-ти имеют пределы. S+ и S- - сходятся.
Обратное неверно. Определение. Если Признак Лейбница сходимости знакочередующегося числового ряда. Схема исследования на абсолютную и словную сходимость.
Док-во. a1-a2+a3-a4+a5-a6+… сгруппируем члены попарно:
с другой стороны: a1-a2+a3-a4+a5-a6+…=a1-(a2-a3)-(a4-a5)-…<a1, т.е. сумма ряда ограничена. V1= a2-a3>0; V2= a4-a5>0; S2n=U1+U2…+Un ↑= a1-V1-V2…-Vn-a2n<a1 ↑ и ограничена последовательностью S2n имеет предел S.
Определение. Если Схема исследования:а) проверяем Функциональные ряд, область сходимости.
совокупность точек сходимости ряда называется областью сходимости ряда. Как правило, по Даламберу.
Степенной ряд. Теорема Абеля. Радиус и интервал сходимости.
от (1) к (2) легко перейти, сделав замену t=x - x0 Теорема Абеля. а) если x1 – точка сходимости ряда (2), то " x: |x|<|x1| - ряд сходится.
б) если x2 – точка расходимости ряда (2), то " x: |x|>|x2| - ряд расходится.
Свойства степенных рядов. Почленное дифференцирование и интегрирование степенного ряда.
Ряды Тейлора и Маклорена. Остаточный член ряда Тейлора, его структура. Пусть есть f(x) такая, что $ f(x0) f’(x0)… f(n)(x0) тогда ряд Тейлора для f(x) в точке x0
Если f(x) – бесконечно дифференцируема, то ряд Тейлора для нее бесконечен. Если x0=0 – такой ряд называется рядом Маклорена.
Найдем оценку для
35. Разложение в ряд Маклорена показательных функций f(x)=ex, f(x)=chx, f(x)=sh(x)
36. Разложение в ряд Маклорена тригонометрических функций: f(x)=sinx, f(x)=cosx.
Формула Эйлера.
выделим действительную и мнимую части
38. Разложение в ряд Маклорена функций
39. Разложение в ряд Маклорена логарифмических функций: y=ln(1+x), y=ln(1-x), y=ln
40. Разложение в ряд Маклорена биномиальной функции f(x)=(1+x)m, где m- произвольное действительное число.
41. Разложение в ряд Маклорена обратных тригонометрических функций: y=arctgx; y=arcsinx.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.118.236 (0.006 с.) |





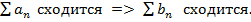

 сходится и
сходится и  , тогда
, тогда  , т.к.
, т.к.


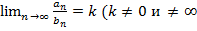 т.е. " e $ N: при a≥N
т.е. " e $ N: при a≥N  . Выберем e и возьмем N:
. Выберем e и возьмем N:  Просуммируем.
Просуммируем. Если
Если  сход => меньший ряд тоже сход.=>
сход => меньший ряд тоже сход.=>  сход.=>
сход.=>  сход. Обратное (расх.) аналогично.
сход. Обратное (расх.) аналогично.




 , т.е. " e $ N, "n≥N;
, т.е. " e $ N, "n≥N;  ; выберем e<q и раскроем модуль.
; выберем e<q и раскроем модуль.  => просуммируем
=> просуммируем , тогда 1) q<1 выберем e так, что q+e<1, тогда правый сход, как геометрический и
, тогда 1) q<1 выберем e так, что q+e<1, тогда правый сход, как геометрический и 


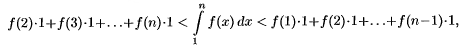


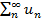 => сходится и исходный ряд.
=> сходится и исходный ряд.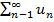 .
.

 - числовой ряд, содержащий бесконечное число положительных и бесконечное число отрицательных рядов, называется знакопеременным.
- числовой ряд, содержащий бесконечное число положительных и бесконечное число отрицательных рядов, называется знакопеременным.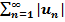
 сход =>
сход => 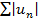 существует. S+ и S- возрастают соответственно, причем S+≤ Sn и S- ≤Sn, т. о. последовательности S+ и S- и ограничены Sn
существует. S+ и S- возрастают соответственно, причем S+≤ Sn и S- ≤Sn, т. о. последовательности S+ и S- и ограничены Sn - разность сходящихся рядов сходится.
- разность сходящихся рядов сходится. сходится, если: а) |an|¯; б)
сходится, если: а) |an|¯; б) 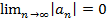


 сход, а
сход, а  расх., такая сходимость называется условной.
расх., такая сходимость называется условной.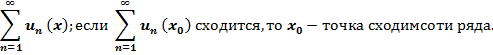








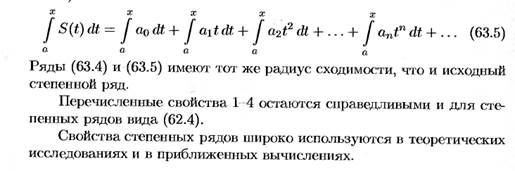
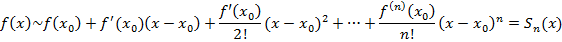
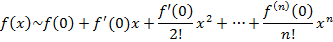



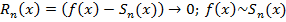



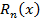


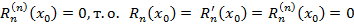
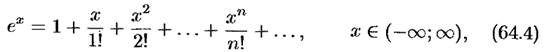








 и
и  .
.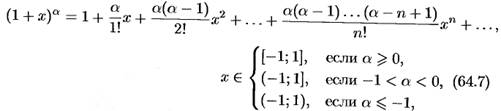
 , предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
, предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
 тогда
тогда
 .
.

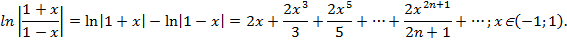


 , предполагая, что в формуле (64.7) a= - 1; x=-x, тогда
, предполагая, что в формуле (64.7) a= - 1; x=-x, тогда