
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные элементарные функции и их графикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Степенная функция у = хα, где где α – действительное число. Например,
Показательная функция
Логарифмическая функция
Тригонометрические функции
Обратные тригонометрические функции
Производные основных элементарных функций
1.
3. 5.
7.
9.
11. 13. 15.
Основные правила дифференцирования
1. 3.
где С – постоянная величина и функции
Свойства неопределенных интегралов
1. 2. 3. 4. где
Таблица основных интегралов
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Формула Ньютона-Лейбница для вычисления определенного интеграла:
где Свойства определенного интеграла 1. 2. 3. 4. 5.
6. Если
Площадь плоской фигуры
где у = f2 (x), y = f 1(x) – уравнения верхней и нижней границ фигуры; х = а, х = b – уравнения левой и правой границ фигуры. Формулы комбинаторики
Классическое определение вероятности:
где m – число благоприятных исходов опыта; n – число всех равновозможных исходов
Относительная частота события: Р *(А) = где m – число наступлений события А; n – число всех проведенных испытаний Теорема сложения вероятностей несовместных событий: Р (А1+А2+…+Аn) =Р (А1) +Р (А2) +…+Р (Аn). Теорема умножения вероятностей двух зависимых событий: Р (А Теорема умножения вероятностей независимых событий:
Теорема сложения вероятностей двух совместных событий:
Вероятность противоположного события:
Вероятность появления хотя бы одного из событий: P (A Треугольник
a, b, с – длины сторон треугольника; h – высота треугольника; γ – угол между сторонами a и b; r – радиус вписанной окружности; R – радиус описанной окружности;
Прямоугольный треугольник
a, b – катеты; c – гипотенуза;
Равносторонний треугольник
a, b – длины сторон прямоугольника;
S = a · b – площадь прямоугольника.
Квадрат
a – длина стороны квадрата;
S = a 2 , Параллелограмм
a, b – длины сторон параллелограмма;
h – длина высоты параллелограмма;
Ромб
a – длина стороны ромба; h – длина высоты ромба; α – угол между сторонами ромба; d 1, d 2 – длины диагоналей;
Трапеция
a, b – длины оснований трапеции; c, d – длины боковых сторон трапеции; h – длина высоты трапеции;
Окружность и круг
r – радиус круга, окружности;
d – диаметр круга, окружности;
Свойства вписанных, описанных фигур
Описанная вокруг треугольника ABC окружность имеет центр в пересечении перпендикуляров к серединам сторон.
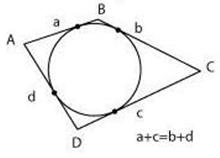
Четырехугольник можно вписать в окружность, если суммы его противоположных углов равны 1800.
Четырехугольник можно описать вокруг окружности, если суммы длин его противоположных сторон равны. Куб
a – ребро куба;
Прямоугольный параллелепипед
a – длина основания; b – ширина основания; h – высота параллелепипеда;
Призма
h – высота призмы;
Пирамида
h – высота пирамиды;
Усеченная пирамида
h – высота усеченной пирамиды;
Цилиндр
R – радиус основания цилиндра; h – высота цилиндра;
Конус
R – радиус основания; h – высота конуса; l – образующая конуса;
Усеченный конус
R – радиус нижнего основания; r – радиус верхнего основания; H – высота усеченного конуса; l – образующая конуса;
Шар, сфера
R – радиус шара, сферы;
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.007 с.) |





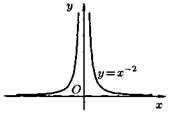

 , где a >0, a ≠ 1.
, где a >0, a ≠ 1.
 , где a >0, a ≠ 1.
, где a >0, a ≠ 1.



 .
.








 . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. . 12.
. 12. 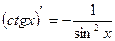 .
. . 14.
. 14. 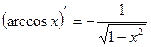 .
. . 16.
. 16.  .
. . 2.
. 2.  .
. . 4.
. 4. 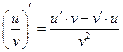 ,
, и
и  имеют производные.
имеют производные.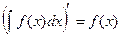 .
. .
. , где
, где  .
. ,
, , С – произвольная постоянная.
, С – произвольная постоянная. .
. .
. , где п ≠-1.
, где п ≠-1. .
. , где а >0, а ≠1.
, где а >0, а ≠1. .
.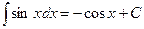 .
. .
. .
. .
. .
. .
. .
. , где а ≠0.
, где а ≠0. , где -1< x <1.
, где -1< x <1. .
. .
. , где а ≠0.
, где а ≠0. , где а ≠0.
, где а ≠0.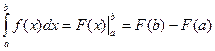 ,
, .
. , где
, где 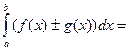

 .
.
 .
. +
+  , где
, где  .
. на отрезке
на отрезке  и
и  , то
, то 
 .
.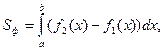

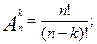

 ,
, ,
, .
. .
.

 +A
+A  +A…+A
+A…+A 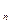 ) = 1– P (
) = 1– P (
 ).
).
 – периметр треугольника;
– периметр треугольника; – полупериметр треугольника;
– полупериметр треугольника; – площадь треугольника;
– площадь треугольника; – формула Герона;
– формула Герона; – площадь треугольника по двум сторонам и углу между ними;
– площадь треугольника по двум сторонам и углу между ними; – площадь треугольника по тремсторонам и радиусу описанной окружности;
– площадь треугольника по тремсторонам и радиусу описанной окружности; – площадь треугольника по трем сторонам и радиусу вписанной окружности.
– площадь треугольника по трем сторонам и радиусу вписанной окружности.
 – теорема Пифагора;
– теорема Пифагора; – площадь прямоугольного треугольника;
– площадь прямоугольного треугольника; ;
;  ;
;  – соотношения в прямоугольном треугольнике;
– соотношения в прямоугольном треугольнике; – радиус описанной около прямоугольного треугольника окружности.
– радиус описанной около прямоугольного треугольника окружности.
 ,
,  – радиусы вписанной и описанной окружностей;
– радиусы вписанной и описанной окружностей; – площадь равностороннего треугольника.
– площадь равностороннего треугольника. 
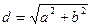 – диагональ прямоугольника;
– диагональ прямоугольника; – периметр прямоугольника;
– периметр прямоугольника;
 – длина диагональ квадрата;
– длина диагональ квадрата; – периметр квадрата;
– периметр квадрата; – формулыплощади квадрата.
– формулыплощади квадрата.
 – площадь параллелограмма;
– площадь параллелограмма; – площадь параллелограмма по двум сторонам и углу между ними.
– площадь параллелограмма по двум сторонам и углу между ними.
 ,
,  – формулы площади ромба.
– формулы площади ромба.
 – периметр трапеции;
– периметр трапеции; – площадь трапеции.
– площадь трапеции.
 ,
,  – формулы площади круга;
– формулы площади круга; – длина окружности.
– длина окружности.


 – диагональ куба;
– диагональ куба; – площадь одной грани куба;
– площадь одной грани куба; – площадь полной поверхности куба;
– площадь полной поверхности куба;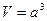 – объем куба.
– объем куба.
 – диагональ параллелепипеда;
– диагональ параллелепипеда; – площадь основания;
– площадь основания; – объем прямоугольного параллелепипеда.
– объем прямоугольного параллелепипеда.
 – площадь полной поверхности призмы;
– площадь полной поверхности призмы; – объем призмы.
– объем призмы.
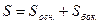 – площадь полной поверхности пирамиды;
– площадь полной поверхности пирамиды; – объем пирамиды.
– объем пирамиды.
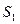 – площадь нижнего основания пирамиды;
– площадь нижнего основания пирамиды;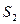 – площадь верхнего основания пирамиды;
– площадь верхнего основания пирамиды; +
+ 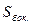 – площадь полной поверхности усеченной пирамиды;
– площадь полной поверхности усеченной пирамиды;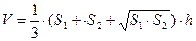 – объем усеченной пирамиды.
– объем усеченной пирамиды.
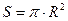 – площадь основания;
– площадь основания; – площадь полной поверхности цилиндра;
– площадь полной поверхности цилиндра; – объем цилиндра.
– объем цилиндра.
 – площадь основания конуса;
– площадь основания конуса; – площадь боковой поверхности конуса;
– площадь боковой поверхности конуса; – объем конуса.
– объем конуса.
 – площадь нижнего основания конуса;
– площадь нижнего основания конуса;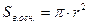 – площадь верхнего основания конуса;
– площадь верхнего основания конуса; – площадь боковой поверхности;
– площадь боковой поверхности; – объем конуса.
– объем конуса.
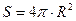 – площадь сферы;
– площадь сферы; – объем шара.
– объем шара.


