
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 32. Координаты и векторыСодержание книги
Поиск на нашем сайте
Задание 71. Найдите координаты заданной точки по координатам других точек.
1. На оси Ох найти точку, равноудаленную от точек C (3; -2; 4) и В (0; 5; -1).
2. На оси Оу найти точку, равноудаленную от точек А (-2; 3; 4) и D (5; 0; -1). 3. На оси Оz найти точку, равноудаленную от точек M (4; -2; 3) и N (-1; 5; 0). 4. На оси Ох найти точку, равноудаленную от точек А (4; -1; 5) и В (1; 6; 0). 5. На оси Оу найти точку, равноудаленную от точек E (3; -2; 4) и F (0; 1; -1). 6. На оси Оz найти точку, равноудаленную от точек А (-1; 0; 2) и В (0; -1; 0). 7. На оси Ох найти точку, равноудаленную от точек C (3; -2; 4) и D (2; 3; -1). 8. На оси Оу найти точку, равноудаленную от точек А (0; -2; -4) и В (0; -5; -1). 9. На оси Оz найти точку, равноудаленную от точек M (3; -5; 0) и N (0; 5; 1). 10. На оси Ох найти точку, равноудаленную от точек А (-1; 4; 0) и В (0; 2; -1). 11. На оси Оу найти точку, равноудаленную от точек C (6; -2; 4) и D (4; 1; 1).
12. На оси Оz найти точку, равноудаленную от точек N (3; 0; 0) и N (0; 3; -2). 13. На оси Ох найти точку, равноудаленную от точек F (2; 2; 4) и K (0; 5; -1).
14. На оси Оу найти точку, равноудаленную от точек А (3; -2; 4) и В (6; 0; -4). 15. На оси Оz найти точку, равноудаленную от точек C (-1; 2; 0) и D (0; 4; -1). 16. На оси Ох найти точку, равноудаленную от точек N (2; -2; 4) и M (0; -1; 1). 17. На оси Оу найти точку, равноудаленную от точек А (5; 2; -4) и В (0; 0; -1). 18. На оси Оz найти точку, равноудаленную от точек D (3; 1; 4) и C (0; 1; 0). 19. На оси Ох найти точку, равноудаленную от точек S (-3; 2; 1) и В (0; -4; -1). 20. На оси Оу найти точку, равноудаленную от точек M (0; -2; 4) и N (-4; 0; 1). 21. На оси Оz найти точку, равноудаленную от точек E (3; -4; 4) и В (0; 6; 0). 22. На оси Ох найти точку, равноудаленную от точек А (3; -2; 9) и В (0; 5; 4). 23. На оси Оу найти точку, равноудаленную от точек C (0; 2; -4) и D (1; 0; -5).
24. На оси Оz найти точку, равноудаленную от точек F (1; 0; 5) и S (-3; 2; 0). 25. На оси Ох найти точку, равноудаленную от точек А (0; 2; 4) и В (0; -2; 1). Задание 72. Даны три вершины параллелограмма ABCD. Найдите координаты четвертой вершины.
1. А (1; 0; 1), В (-1; 5; 0), С (2; 6; 0). 2. А (2; 0; 1), В (-2; 5; 3 ), С (1; 3; 0). 3. А (1; 0; 2), В (-1; 5; 1), С (2; 4; 1). 4. А (1; 0; 1), В (-1; 5; 0), С (1; 3; 0). 5. А (1; -1; 1), В (-1; 4; 0), С (1; 2; 0). 6. А (2; 0; 1 ), В (0; 5; 0), С (2; 3; 0). 7. А (1; 0; 1), В (-1; 6; 0), С (2; 6; 0). 8. А (1; 0; 3), В (-1; 5; 2), С (2; 4; 2). 9. А (-1; 0; 1), В (-3; 6; 0), С (0; 6; 0). 10. А (1; 0; 1), В (-1; 5; 0), С (1; 5; 0). 11. А (1; 0; -1), В (-1; 5; -2), С (1; 5; -2). 12. А (3; 0; 1), В (1; 5; 0), С (3; 5; 0). 13. А (1; 0; 1), В (-1; 5; 1), С (2; 6; 0). 14. А (1; -3; 1), В (-1; 2; 1), С (2; 3; 0). 15. А (3; 0; 1), В (1; 5; 1), С (4; 6; 0). 16. А (4; 0; 1), В (2; 5; 0), С (5; 1; 3). 17. А (1; 0; 1), В (-1; 5; 0), С (2; 6; 0). 18. А (3; 0; 1), В (1; 5; 0), С (4; 2; -1). 19. А (1; 0; 0), В (-1; 5; 1), С (2; 4; 2). 20. А (1; 0; 1), В (-1; 5; 2), С (2; 6; 1). 21. А (1; -1; 1), В (-1; 6; 2), С (2; 7; 1). 22. А (1; 1; 1), В (-1; 6; 2), С (2; 7; 1). 23. А (0; 0; 0), В (1; 4; 1), С (-1; 4; 1). 24. А (-1; 0; 0), В (0; 4; 1), С (-2; 4; 1). 25. А (-1; 0; 1), В (0; 4; 2), С (-2; 4; 2). Задание 73. Даны координаты точек А, В, С. Найдите: а) длины векторов АВ и АС; б) скалярное произведение векторов АВ и АС; в) угол между векторами АВ и АС. 1. А (1; 0; -1), В (-1; 4; -2), С (1; 5; -2). 2. А (3; 0; 1), В (1; 5; 0), С (3; 5; 0). 3. А (1; 0; 1), В (-1; 5; 1), С (2; 6; 0). 4. А (1; -3; 1), В (-1; 2; 1), С (2; 3; 0). 5. А (3; 0; 1), В (1; 5; 1), С (4; 6; 0). 6. А (4; 0; 1), В (2; 5; 0), С (5; 1; 3). 7. А (1; 0; 1), В (-1; 5; 0), С (2; 6; 0). 8. А (3; 0; 1), В (1; 5; 0), С (4; 2; -1). 9. А (1; 0; 0), В (-1; 5; 1), С (2; 4; 2). 10. А (1; 0; 1), В (-1; 5; 2), С (2; 6; 1). 11. А (1; -1; 1), В (-1; 6; 2), С (2; 7; 1). 12. А (1; 1; 1), В (-1; 6; 2), С (2; 7; 1). 13. А (0; 0; 0), В (1; 4; 1), С (-1; 4; 1). 14. А (-1; 0; 0), В (0; 4; 1), С (-2; 4; 1). 15. А (-1; 0; 1), В (0; 4; 2), С (-2; 4; 2). 16. А (1; 0; 1), В (-1; 5; 0), С (2; 6; 0). 17. А (2; 0; 1), В (-2; 5; 3 ), С (1; 3; 0). 18. А (1; 0; 2), В (-1; 5; 1), С (2; 4; 1). 19. А (1; 0; 1), В (-1; 5; 0), С (1; 3; 0). 20. А (1; -1; 1), В (-1; 4; 0), С (1; 2; 0). 21. А (2; 0; 1 ), В (0; 5; 0), С (2; 3; 0). 22. А (1; 0; 1), В (-1; 6; 0), С (2; 6; 0). 23. А (1; 0; 3), В (-1; 5; 2), С (2; 4; 2). 24. А (-1; 0; 1), В (-3; 6; 0), С (0; 6; 0). 25. А (1; 0; 1), В (-1; 5; 0), С (1; 5; 0). Задание 74. Найдите координаты центра и радиус сферы, заданной уравнением: 1. х 2 + у 2 + z 2 + 4 х + 6 z – 3 = 0. 2. х 2 + у 2 + z 2 + 4 х –2 у –11 = 0. 3. х 2 + у 2 + z 2 + 4 у –12 = 0. 4. х 2 + у 2 + z 2 + 4 х – 2 z –4 = 0. 5. х 2 + у 2 + z 2 – 10 х – 2 у + 2 z – 2 = 0. 6. х 2 + у 2 + z 2 + 6 х –2 у –6 = 0. 7. х 2 + у 2 + z 2 + 4 х –2 у – 2 z –3 = 0. 8. х 2 + у 2 + z 2 + 2 х + 8 у + 2 z –7 = 0. 9. х 2 + у 2 + z 2 –4 х +2 у + 6 z –11 = 0. 10. х 2 + у 2 + z 2 – 10 х – 2 у + 6 z + 10 = 0. 11. х 2 + у 2 + z 2 + 4 х –2 у – 6 z + 5 = 0. 12. х 2 + у 2 + z 2 + 8 х + 6 у = 0. 13. х 2 + у 2 + z 2 + 4 х – 2 z + 1 = 0. 14. х 2 + у 2 + z 2 + 4 х –12 = 0. 15. х 2 + у 2 + z 2 – 8 х – 6 z = 0. 16. х 2 + у 2 + z 2 – 4 х + 2 у + 1 = 0. 17. х 2 + у 2 + z 2 – 4 х +2 у – 2 z –3 = 0. 18. х 2 + у 2 + z 2 + 10 х + 2 у – 2 z – 2 = 0. 19. х 2 + у 2 + z 2 –4 у –12 = 0. 20. х 2 + у 2 + z 2 + 4 х – 12 у –9 = 0. 21. х 2 + у 2 + z 2 + 2 х –10 у – 6 z + 19 = 0. 22. х 2 + у 2 + z 2 + 4 х –2 у – 6 z –11 = 0. 23. х 2 + у 2 + z 2 + 10 х + 2 у – 6 z + 10 = 0. 24. х 2 + у 2 + z 2 –4 z –12 = 0. 25. х 2 + у 2 + z 2 + 4 х – 6 z – 3 = 0. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Алгебра и начала анализа. Учебник для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под ред. А.Н. Колмогорова. – 14-е изд. – М.: Просвещение, 2010. – 384 с. 2. Геометрия, 10–11: Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 14-е изд. – М.: Просвещение, 2010. – 206 с.
Дополнительная
1. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля. Учебник для образовательных учреждений начального и среднего профессионального образования. – М.: Академия, 2010. – 384 с. 2. Максимова О.В. Теория вероятностей и математическая статистика: Учебное пособие для студентов средних специальных учебных заведений. – М.: Издательско-торговая корпорация «Дашков и Ко», 2006. – 320 с.
ПРИЛОЖЕНИЕ
Действия с дробями 1. 3. Формулы сокращенного умножения
1. а2–b2=(a–b)(a+b). 4. a3+b3=(a+b)(a2–ab+b2). 2. (a+b)2=a2+ 2 ab+b2. 5. a3–b3=(a–b)(a2+ab+b2). 3. (a–b)2=a2– 2 ab+b2. 6. (a+b)3=a3+ 3 a2b+ 3 ab2+ b3. 7. (a–b)3=a3–3a2b+3ab2–b3.
Квадратные уравнения
a x2 + b x + c = 0, где а ≠ 0, D=b2– 4 ac – дискриминант уравнения; при D <0 – уравнение не имеет действительных корней; при D =0 – уравнение имеет единственный корень; при D >0 – уравнение имеет два действительных корня
При D >0 a x2 + b x + c = a (x – x 1) (x – x 2). По теореме Виета: Степень и ее свойства
Если
1.
3. 5. 7.
9.
Свойства арифметических корней Если 1. 3. 5. 7. 9. Логарифмы и их свойства
Основное логарифмическое тождество: 1. 2. 3. 4. 5. 6. 7. 8.
Основные тригонометрические тождества
Формулы сложения
Формулы двойного аргумента
Формулы половинного аргумента
Формулы преобразования суммы в произведение
Формулы преобразования произведения в сумму
Обратные тригонометрические функции
Таблица некоторых значений тригонометрических функций
Простейшие тригонометрические уравнения
Частные случаи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.221.171 (0.007 с.) |

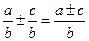 . 2.
. 2.  .
. . 4.
. 4.  .
.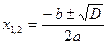 .
.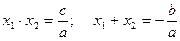 .
. ,
,  , то
, то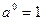 . 2.
. 2.  .
. . 4.
. 4. 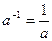
 . 6.
. 6.  .
. . 8.
. 8.  .
. .
. ,
,  . 2.
. 2. 
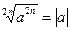 . 4.
. 4.  .
. . 6.
. 6. 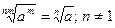 .
.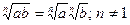 . 8.
. 8. 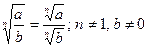 .
. . 10.
. 10.  .
. .
.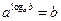 .
. .
. .
. .
. .
. .
. .
. .
.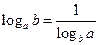 .
.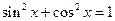 ;
;  ;
; ;
; 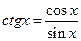 ;
;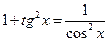 ;
;  .
.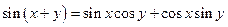 ;
; ;
; ;
;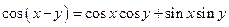 ;
; .
. .
. ;
;  ;
; ;
;  ;
; .
. ;
;  ;
; .
.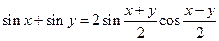 ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; ;
; .
. ;
; ;
;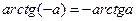 ;
; .
.

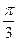


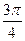





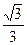



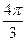


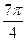

 , где
, где 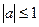
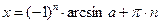 , где
, где 
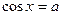 , где
, где  , где
, где 
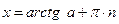 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где 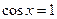
 , где
, где 


