
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория прочности, деформативности и конгруэнции свойствСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОСНОВНЫЕ СВОЙСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
При выборе материала и обосновании целесообразности применения в строительной конструкции учитывают его способность сопротивляться реальным нагрузкам без нарушения сплошности и размеров. Одни материалы успешно сопротивляются сжимающим усилиям, другие — растягивающим, которые возникают под действием нагрузки или других силовых факторов. Аналогичная сопротивляемость материалов характерна при воздействии сил, способных вызвать изгиб, сдвиг, раскалывание и т. п. Материал должен надежно сопротивляться этим воздействующим силам при работе конструкции в эксплуатационный период. Одновременно необходимо, чтобы материал проявлял достаточную стойкость к воздействию физических (например, температуры и ее колебаний, в особенности при переходе ч'ерез 0°С, водной среды и др.) и химических (кислоты, щелочи, солевые растворы и др.) факторов. Нередко одним из главных показателей качества служит способность материала к восприятию технологической обработки, например шлифования, распиливания, раскалывания на части правильной формы и т. п. Следовательно, для обоснованного выбора материала приходится учитывать комплекс его так называемых свойств. Под свойствами строительных материалов понимают их способность определенным образом реагировать на отдельные или совокупные внешние или внутренние воздействия — силовые, тепловые, усадочные, водной или иной среды и т. д. Свойства разделяют на четыре группы: механические, физические, химические, технологические, иногда выделяют еще физико-химические. В совокупности все свойства именуют как технические свойства строительных материалов. Числовые значения свойств получают при лабораторных или полевых испытаниях материалов с помощью соответствующих приборов и аппаратов. Испытания производят с разрушением специально подготовленных образцов или отдельных элементов конструкции или без их разрушения, т. е. адеструктивными методами.
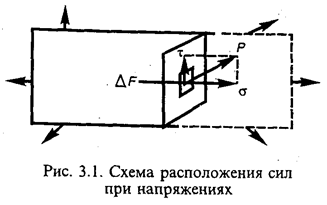
МЕХАНИЧЕСКИЕ СВОЙСТВА Механические свойства выражают способность материала сопротивляться напряжениям силовым (от механических нагрузок), тепловым, усадочным или другим без нарушения установившейся структуры. Чаще всего напряжение обусловлено внутренней механической силой, а его числовая величина определяется как отношение силы к единице площади. Под внутренней подразумевают силу действия частиц, находящихся по одну сторону площадки, на частицы, находящиеся по другую сторону этой площадки (рис. 3.1). Расчетом определяют нормальные (перпендикулярные к площадке) и касательные напряжения, выражаемые в размерности «сила/площадь» (МПа). Механические свойства разделяются на деформационные и прочностные.
Деформационные свойства характеризуют способность материала к изменению формы или размеров без отклонений в величине его массы. Главнейшие виды деформаций — растяжение, сжатие, сдвиг, кручение и изгиб. Все они могут быть обратимыми и необратимыми. Обратимые полностью исчезают при прекращении действия на материал факторов, их вызвавших. Необратимые деформации, или остаточные, называемые также пластическими, накапливаются в период действия этих факторов; после их снятия деформации сохраняются. Обратимые деформации, исчезающие мгновенно и полностью, называются упругими; исчезающие в течение некоторого времени — эластическими. Деформации могут быть также сложными — упруго-пластическими или упруго-вязко-пластическими, если достаточно четко выражены соответственно упругая и пластическая или упругая, эластическая и пластическая части (рис. 3.2).
Рис. 3.2. Графики зависимости деформаций (ε) от времени (τ) действия нагрузок: а — упругая деформация; б — упругоэластическая деформация; в — пластическая деформация; г — упругопластическая деформация
На характер и величину деформации влияют не только величина механического нагружения, но и скорость приложения этой нагрузки, а также температура материала. Как правило, с повышением скорости нагружения, а следовательно, деформирования, а также с понижением температуры материала деформации по своему характеру приближаются к упругим и упруго-пластическим, уменьшаясь по своей абсолютной величине. Пластические деформации, медленно нарастающие без увеличения напряжения, характеризуют текучесть материала. Пластическая деформация, медленно нарастающая в течение длительного времени под влиянием силовых факторов, не способных вызвать остаточную деформацию за обычные периоды наблюдений, называется деформацией ползучести, а процесс такого деформирования — ползучестью, или крипом. Явление ползучести выражается в непрекращающемся изменении размера тела (образца) под влиянием 'растягивающих или сжимающих силовых воздействий (напряжений ниже предела прочности) при постоянной температуре (ниже.температуры плавления). Ее обычно выражают в единицах скорости деформации, т. е. как относительное изменение размеров образца (в мм) за время (в ч): τ= (∆l/l)∙(1/ τ), где ∆l — линейное изменение образца, мм, за время τ, ч; l — начальная длина, мм. Деформационные свойства строительных материалов, как и других тел, обусловливаются периодом, или временем релаксации. Релаксацией называется процесс самопроизвольного падения внутренних напряжений в материале, связанных с молекулярным перемещением при условии, что начальная величина деформации остается неизменной, например зафиксированной жесткими связями. Характер начальной деформации в период релаксации напряжений может измениться, например, из упругой постепенно перейти в необратимую (пластическую), что связано с переориентацией внутримолекулярной структуры. Время, или период, релаксации определяет продолжительность релаксационных процессов, в результате которых первоначальная величина напряжений при строго зафиксированной деформации снизилась в е раз (е — основание неперовых логарифмов, равное 2,718...). Так, например, если у материала в виде образца напряжение было равно 5,0 МПа, а возникшая деформация под влиянием этого напряжения была жестко зафиксирована, то время (θ с), за которое напряжение самопроизвольно снизилось до величины 5,0:2,718 = 1,85 МПа, называется временем, или периодом, релаксации, выражаемым в секундах или минутах. Эта величина — важная характеристика строительных материалов: чем она меньше, тем более деформативным является материал. Нередко время релаксации зависит от температуры материалов в момент испытания и скорости приложения нагрузки, являясь непостоянной величиной. При весьма малой продолжительности (τ с) действия сил (или кратковременном наблюдении) по сравнению с величиной времени релаксации (τ << 6) все материалы (тела) ведут себя как упругохруп-кие тела и имеют полную обратимость деформаций, если, конечно, напряжения не нарушают их сплошности. Однако наиболее типичным случаем деформации хрупких тел (материалов) является отсутствие структурных изменений, а упругая энергия, затрачиваемая на деформацию, не успевает рассеиваться под влиянием релаксационных процессов. У упругохрупких тел возможно накопление малой упругой энергии, а за счет местных разрушений структуры происходит частичная релаксация напряжений. Приближенным значением меры хрупкости служит ψ = εy/εпред и при ψ = 1—0,8 разрушение от нагружения происходит без торможения трещин, внезапно. При очень длительных (τ >> 9) наблюдениях за действием нагрузки (по сравнению с временем релаксации) материал подобно жидкости течет. При очень коротких наблюдениях (по сравнению с временем релаксации) даже жидкий материал проявляет хрупкость твердого кристаллического тела. Так, например, при весьма коротком времени действия силы на воду, время релаксации которой равно порядка 10-11 с, она ведет себя как кристаллическое твердое тело; при весьма длительном периоде действия сил (или наблюдения) природный камень в виде горных пород, время релаксации которого равно 1010 с, ведет себя как текучая жидкость. Но эти крайние условия не встречаются в практике строительства и эксплуатации конструкций зданий и сооружений, поэтому вода всегда кажется жидкой, а камень — твердым. Однако многие материалы остаются весьма чувствительными к различию между временем действия нагрузки и временем релаксации, особенно при повышенных температурах, когда процесс релаксации напряжений в некоторых материалах заметно интенсифицируется, особенно при местных (локальных) перенапряжениях в материале. Кроме времени релаксации, в расчетах пользуются коэффициентом у релаксации, показывающим долю спада напряжений за определенный период времени: ψ = στ/σ0, где στ — напряжение в момент времени τ при постоянной деформации; σ0 — начальное напряжение. Коэффициент релаксации позволяет расчетным путем определить релаксационную характеристику с помощью опытных значений деформации ползучести, точнее —скорости ползучести, получаемых менее трудоемким измерением, чем релаксации напряжений. С некоторым приближением к опытным данным можно воспользоваться зависимостью: ln ψ = -φ, где φ — коэффициент ползучести, равный ετ/ε0 = Е0/εS; ετ — деформация ползучести в момент времени τ при постоянном напряжении σ0; ε0 — начальная упругая деформация, равная σ0/Е0; Е0 — начальный модуль упругости, равный σ0/ ε0; εS — удельная деформация ползучести в момент времени τ, равная ετ/σ0. Прочность характеризует способность материала в определенных условиях и пределах, не разрушаясь, сопротивляться внутренним напряжениям и деформациям, возникающим под влиянием механических, тепловых и других напряжений. Типичными прочностными характеристиками служат предел упругости, предел текучести и предел прочности при воздействии сжимающих, растягивающих или других видов усилий. Пределу упругости соответствует напряжение материала при максимальной величине упругой деформации; пределу текучести — постоянное напряжение при нарастании пластической деформации; пределу прочности — максимальное напряжение в момент разрушения материала (рис. 3.3). Эти характеристики прочности относятся к кратковременному действию приложенной нагрузки (табл. 3.1). При длительном действии нагрузки возрастает опасность нарушения структуры материала. Даже сравнительно малые величины напряжения (например, от собственной массы) могут вызвать ползучесть и заметное ухудшение структуры с потерей прочности. Нередко измеряют длительную прочность материала не только при статической (неподвижной), но и динамической нагрузках. Материал может резко терять свою прочность после приложения к нему вибрационной нагрузки, что обусловлено усталостью — накоплением неотрелаксированных напряжений и необратимых микродефектов в структуре. Соответствующая прочность материала называется усталостной и определяется специальным испытанием образцов.
Таблица 3.1. Физико-механические свойства некоторых материалов
В целом упомянутые выше характеристики прочности по своей сущности относятся к условным по двум причинам. Во-первых, они не учитывают фактора времени, что с некоторым приближением можно допустить только в отношении хрупких материалов. Во-вторых, приборы, размеры и форма образцов, скорость приложения нагрузки на прессе и другие исходные параметры методов испытания материала на прочность приняты условными. Поэтому материал может иметь различную величину показателя прочности в зависимости от размера образца, скорости приложения нагрузки и конструкции прибора, на котором испытывались образцы. Например, чем меньше размеры «кубика», больше скорость приложения нагрузки (или скорости деформации), тем выше получаемая величина предела прочности при испытании на сжатие. В упругой области деформаций действует закон Гука: σ = Е∙ε, где σ — напряжение, МПа; ε — относительная упругая деформация; Е — модуль упругости материала, МПа. Если относительная деформация ε, выражающая отношение прироста деформации ∆l к первоначальной длине образца l, т. е. ∆l /l окажется равным единице (ε = 1), то Е = σ. Отсюда следует, что модуль упругости по своему физическому смыслу численно равен напряжению, которое потребовалось приложить к материалу (образцу), чтобы вызвать относительную деформацию ε = 1 (что возможно, когда приращение ∆l = l), т. е. когда было удвоение длины образца при условии сохранности упругих свойств материала. В реальных строительных материалах (кроме резины) величина упругой деформации всегда гораздо меньше, составляя у стали 1—1,5 %, а у хрупких она и вовсе приближается к нулю. Численные значения величины модуля упругости и прочности определяют как с разрушением образцов, например при испытании под прессом, так и неразрушающими (адеструктивными) методами. Распространены следующие адеструктивные методы их измерения: акустические, магнитные и электромагнитные, механические, радиометрические, рентгеновские и электрические. Они основаны на прямых и обратных закономерностях между физическими значениями, получаемыми при испытании неразрушающим прибором, и традиционными показателями свойств. Зависимости выражаются в виде формул, таблиц, тарировочных графиков. Измерения становятся более эффективными при комплексном использовании адест-руктивных методов измерения с получением двух или нескольких физических характеристик. К комплексным методам относится совместное применение механического и ультразвукового методов или радиометрического и ультразвукового и других для определения предела прочности и модуля упругости, контроля качества и дефектоскопии, однородности по различным показателям (прочности, влажности, толщине защитного слоя и др.). Эти методы весьма эффективны при контроле за сохранением оптимальности структуры материалов и изделий по однородности, минимуму дефектов, плотности, континуальности пространственной сетки вяжущего вещества или жидкостной оболочки свежеизготовленного монолита, минимального количества вяжущего вещества или другим обязательным ее параметрам. В частности, набору параметров оптимальной структуры соответствует наиболее широкий спектр частот ультразвукового сигнала, а также наибольшая амплитудная характеристика. Альтернативой условным методам определения прочности имеются инвариантные, независимые от обстановки опыта. К инвариантным характеристикам прочности относятся предельное напряжение сдвига (Рк), структурная вязкость и другие, определяемые с помощью построения реологических кривых по данным измерений на вискозиметрах, пластометрах и других приборах. Принцип действия таких приборов основан на истечении массы через капилляр заданного диаметра или на погружении в вещество металлического конуса, шара или других тел. При испытаниях осуществляется чистый и однородный сдвиг частиц вещества относительно друг друга в плоскостных или цилиндрических (коаксиальных) приборах (вискозиметрах) и достаточно четко устанавливается, что прочностные характеристики существенно зависят от продолжительности действия механического усилия, являются типичными кинетическими величинами. Кроме прочности технической или реальной, определяемой с помощью условных или инвариантных приборов, существует прочность, определяемая вычислением и поэтому называемая теоретической. Простейший метод оценки теоретической прочности твердых тел был, в свое время, предложен Поляки. Так, если для разрыва стержня сечением 1 м2 потребовалось приложить напряжение сто, а атомные плоскости при этом удалились друг от друга на величину а, адекватную порядку параметра кристаллической решетки, то работа выразилась как σ0∙а. При разрыве образовались две новых поверхности площадью 2 м2, а затраченная работа перешла в свободную поверхностную энергию. Последнюю можно обозначить как g и выразить в Дж/м2. Следовательно, σ0∙а = 2%. Отсюда искомая теоретическая прочность σ0 = 2g/а. Существуют и другие методы определения теоретической прочности хрупких твердых тел, например по теплоте сублимации (переходе вещества из твердого состояния в газообразное без превращения в жидкость); по методу Поляни—Орована (из сил молекулярного взаимодействия) и др. Установлено, что независимо от метода вычисления результаты дают близкие значения теоретической прочности для твердых тел: σ0 ≈ 0,1Е. Учитывая высокие значения модуля упругости (табл. 3.2), становится очевидным, что теоретическая прочность твердых тел и кристаллов также очень велика. Что же касается технической (реальной) прочности, то она в 100—1000 раз, т. е. на два-три десятичных порядка, ниже теоретической прочности (см. табл. 3.2). Большое различие между теоретической и реальной прочностью материалов объясняется дефектностью микроструктуры, т. е. наличием микротрещин, пор и т. п. Чем крупнее образцы твердых тел, принятых для испытания, тем больше концентрируется в них дефектов, а поэтому их реальная прочность ниже, т. е. действует обратная зависимость прочности от размера изделий (масштабного фактора). Таблица 3.2. Свойства некоторых металлических и неметаллических материалов
Наиболее обстоятельно метод расчета реальной (технической) прочности хрупких твердых тел исследовал Гриффите. Им предложена формула для расчета этой прочности материала, имеющего микротрещину:
где g и Е — соответственно свободная поверхностная энергия образца и модуль упругости материала, l — длина поперечной микротрещины в образце, составляющая обычно к моменту разрушения образца несколько микрон или более; β — числовой коэффициент, зависящий от вязкости и характера материала: наличия кристаллической и аморфной фаз, их количественного соотношения, дефектов в кристаллической решетке (вакансий, дислокации), микропор в аморфной части структуры. Следует отметить, что прочность больше, чем некоторые другие свойства материала, проявляет чувствительность к явлениям и процессам формирования и изменения структуры, особенно кристаллической. Прочность является структурно-чувствительным свойством, поэтому ее можно изменять в необходимом направлении путем соответствующих корректив структуры на микро- или макроуровне; уменьшения дефектов; введения добавок, например кристаллических затравок; повышения дисперсности новообразующихся фаз; оптимизации структуры, изменения пористости и размера пор и др. Дополнительными характеристиками механических свойств материалов служат твердость, истираемость, ударная вязкость. Твердость выражает способность материала сопротивляться проникновению в него более твердых тел, например при испытании на склерометрах путем вдавливания стального шарика или стального конуса, царапании резцом, сверлении, ударе молотком, пулевом вы стреле и пр. Эти испытания дают условные значения твердости либо только качественные, например по следу царапания, либо также и количественные — по глубине или площади отпечатка с учетом приложенной нагрузки. Нередко стремятся перейти от полученного значения твердости к величине прочности. Устанавливаемые отношения между твердостью и прочностью тем менее точны, чем пластичнее материал. Только у хрупких тел царапание можно более или менее надежно сравнивать с прочностью, поскольку оба этих свойства обусловлены в основном сцеплением между микрочастицами материала. Нередко о твердости судят также по потере массы образцов при истирании на металлических кругах с добавлением абразивных порошков. Более сложным свойством, включающим прочность и твердость, служит износ. Об износостойкости материала судят по испытанию пробы определенной массы во вращающемся барабане с металлическими шарами или без шаров, в течение определенного периода времени или определенной частоты вращения. Чем больше измельчается проба, тем, следовательно, и больше ее износ (в %). Ударная вязкость характеризует способность материала сопротивляться сосредоточенным ударным нагрузкам и определяется количеством работы, затрачиваемой на излом образца в фиксированном с помощью насечки месте. Работа, отнесенная к площади поперечника образца, характеризует единичную ударную работу на излом, называемую удельной ударной вязкостью. Она имеет практическое значение при оценке качества металлов, асбестоцементных изделий, например кровельных листов и плит. ФИЗИЧЕСКИЕ СВОЙСТВА
Строительные материалы обладают комплексом физических свойств, т. е. способностью реагировать на воздействие физических факторов —гравитационных, тепловых, водной среды, акустических, электрических, излучения (ядерного, рентгеновского и др.). Ниже рассмотрены некоторые свойства, методы и приборы для их оценки в числовых показателях. Средняя плотность характеризует массу единицы объема материала в естественном состоянии (вместе с порами). Эта важная физическая характеристика определяется путем деления массы т образца на его объем уо и выражается ρ0 = m/ν 0 в г/см3, кг/м3 или кг/дм3. Для точного измерения объема удобнее принимать образцы правильной геометрической формы, хотя имеются несложные приемы измерения объема образцов и неправильной формы. При влажных образцах отмечается величина влажности, при которой определялась средняя плотность. Среднюю плотность рыхлых материалов, например песка, щебня, гравия, называют насыпной плотностью. В ее величине отражается влияние не только пор в каждом зерне или куске, но и межзерновых пустот в рыхлом насыпанном объеме материала. Истинная плотность — масса единицы объема однородного материала в абсолютно плотном состоянии, т. е. без учета пор, трещин или других полостей, присущих материалу в его обычном состоянии. Определяется как отношение массы т материала, выраженной в г или кг, к объему v его в абсолютно плотном состоянии: ρ = m/ν. Размерность истинной плотности г/см3, кг/м3. Величина ρ, как правило, больше ρ0, так как подавляющее количество материалов содержат поры, трещины, каверны. Пористость — степень заполнения объема материала порами: определяют ее по формуле П = [(ρ – ρ 0)100]/ ρ (в %). Если требуется выяснить, являются ли поры замкнутыми или сквозными, как распределены они в объеме материала по своим размерам, какое имеется реальное соотношение пор разных диаметров, тогда производят дополнительные исследования с применением специальных методов: сорбционного, ртутной порометрии, капиллярного всасывания и др. Величина пористости и размер пор в значительной мере влияют на прочность материала. При одном и том же веществе строительный материал тем слабее сопротивляется механическим силам, усилиям другого происхождения (тепловым, усадочным и др.), чем больше пор в его объеме. Для некоторых разновидностей материалов существуют ярко выраженные зависимости. Так, например, чем меньше средняя плотность (больше пористость), тем меньше прочность материала. В самом общем виде зависимость прочности от пористости выражена формулой: Rn = R0(1—АП), где Rn и R0 -прочности соответственно пористого и беспористого материала; А — коэффициент структуры, отражающий ее пористость; П — общая пористость материала (вещества) в долях единицы. Наименьшее значение коэффициента А = 1,0—1,1 соответствует оптимальным структурам с содержанием пор П до 0,02—0,03. Формула показывает возможность приближения значений Rn и R0 путем изменения структуры материала (вещества). Известны многочисленные эмпирические формулы, полученные 13 опытных данных применительно к различным материалам, в той или иной мере воспроизводящие указанную выше зависимость Rn = f (П). Опытные данные показывают, что при увеличении пористости от нуля до 20 % прочность снижается почти линейно. Впрочем возможны и «аномалии», особенно среди обжиговых ИСК, когда прочность повышается с повышением пористости, например при обжиге шпинелидных огнеупоров. От пористости зависят и другие качественные характеристики, например способность проводить теплоту и звук, поглощать воду. От пор отличаются полости в структуре, именуемые пустотами. Они значительно крупнее пор, отчетливо видны и расположены между зернами насыпного материала. В отличие от пор вода в пустотах, особенно в широкополостных, не задерживается. На величину прочности влияют и размеры пор. Она возрастает с уменьшением размера пор. Мелкозернистые материалы и, следовательно, мелкопористые, имеют повышенную прочность по сравнению с крупнозернистыми. При этом в меньшей мере снижают прочность закрытые поры, а не открытые, сквозные, обычно по своей форме остроконечные. Имеет значение и местоположение пор. В крупных зернах заполнителя они для прочности менее опасны по сравнению с порами в вяжущей, матричной части конгломерата или расположенными в пограничных зонах, нередко именуемыми как структурные поры материала. Прочность зависит также от прочности связующей фазы и межфазовой адгезии. При воздействии статических или циклических тепловых факторов материал характеризуется теплопроводностью, теплоемкостью, температуроустойчивостью, огнестойкостью и другими теплофизическими свойствами. Теплопроводность — способность материала проводить через свою толщу тепловой поток, возникающий под влиянием разности температур на поверхностях, ограничивающих материал. Это свойство характеризуется теплопроводностью X, которая показывает количество теплоты, проходящее через плоскую стенку толщиной 1 м и площадью 1 м2 при перепаде температур на противоположных поверхностях в 1°С в течение 1 ч. Величина λ имеет размерность Вт/(м∙К) и может служить убедительной сравнительной характеристикой при оценке теплозащитных свойств различных изотропных материалов в одномерном температурном поле. Она зависит, главным образом, от пористости материала: содержащийся в порах воздух, особенно в замкнутых порах, является малотеплрпроводной средой. Воздух при атмосферном давлении и температуре +20°С имеет теплопроводность λ = 0,023 Вт/(м∙К), а при температуре +100°С — 0,0306 Вт/(м∙К), при 1000°С — 0,0788 Вт/(м∙К). С повышением температуры теплопроводность большинства строительных материалов увеличивается, что объясняется повышением кинематической энергии молекул, слагающих вещество материала: λt = λ0 (1 + βt), где λt и λ0 — теплопроводность соответственно при температурах t и 0°С; β — температурный коэффициент, который показывает величину приращения коэффициента теплопроводности материала при повышении температуры на 1°С; t -температура материала, °С. Эта формула справедлива только при температурах не выше t = 100°С; при более высоких значениях t величину λtопределяют опытным путем. С увлажнением теплопроводность материала возрастает, так как теплопроводность воды при 20°С равна 0,590 Вт/(м∙К), а при 100°С — 0,656 Вт/(м∙К). Если в порах вода замерзает, то теплопроводность материала еще больше увеличивается, поскольку лед имеет λ = 2,1, т. е. в 4 раза больше, чем вода. В справочной литературе приводятся значения λ различных строительных материалов в сухом состоянии при 20°С; они используются при тепловых расчетах, и для решения практических задач. В качестве примеров следует отметить, что гранит имеет теплопроводность 3,2—3,5, а кирпич керамический 0,80—0,85; бетон тяжелый — 1,0—1,5; минеральная вата, применяемая как утеплитель, — 0,06—0,09; мипора — 0,04— 0,05 Вт/(м∙К) и т. д. Следует отметить, что упомянутые материалы являются гетерогенными системами и в их отношении удобнее для практики квалифицировать так называемую эффективную теплопроводность. Она слагается из процессов передачи теплоты через конденсированные (твердые) фазы, поры (газы) и границы пор с твердым веществом. Эффективная теплопроводность твердых тел равна сумме этих процессов, определяемых экспериментально. Теплоемкость характеризует способность материала аккумулировать теплоту при нагревании, причем с повышением теплоемкости больше может выделяться теплоты при охлаждении материала. Температура в комнате, например, может сохраняться устойчивой более длительный период при повышенной теплоемкости использованных материалов для пола, стен, перегородок и других частей помещения, поглощающих теплоту в период действия отопительной системы. Это свойство материала оценивается с помощью так называемой удельной теплоемкости, которая показывает количество теплоты, необходимое для нагревания 1 кг материала на 1°С. Различают истинную теплоемкость при данной температуре и среднюю — в интервале температур. Удельную теплоемкость С иначе называют коэффициентом теплоемкости и численно определяют из выражения
где Q — количество теплоты, затраченное на нагревание материала; т — масса материала, кг; t2 – t1 — разность температур материала до и после нагревания, °С. Ее размерность Дж/(кг∙К). Коэффициент теплоемкости воды равен 4,2∙103 Дж/(кг∙К). Строительные материалы в сухом состоянии имеют более низкие значения этого коэффициента, например, каменные материалы (естественные или искусственные) — от 0,75∙103 до 0,94∙103, лесные материалы — от 2,42∙103 до 2,75∙103 Дж/(кг∙К), сталь — 0,5∙103 Дж/(кг-К) и т. п. С увлажнением материала коэффициенты теплоемкости возрастают, вместе с тем возрастают и значения теплопроводности. Иногда требуется знать величину удельной объемной теплоемкости, например при расчете размеров печи. Под этой характеристикой понимается количество теплоты, необходимое для нагревания 1 м3 материала на 1°С. Показатели теплопроводности и теплоемкости позволяют определять величину так называемого коэффициента теплоусвоения, характеризующего способность материала воспринимать теплоту при колебаниях температуры окружающей среды. В формулу для подсчета коэффициента теплоусвоения кроме упомянутых двух тепло-физических значений входят также величины средней плотности и периода колебания температуры. Огнестойкость характеризует способность строительных материалов выдерживать без разрушения действие высоких температур в течение сравнительно короткого промежутка времени (пожара). В зависимости от степени огнестойкости строительные материалы разделяют на несгораемые, трудносгораемые и сгораемые. Несгораемые материалы в условиях высоких температур не подвержены воспламенению, тлению или обугливанию. При этом некоторые материалы почти не деформируются (кирпич, черепица), другие могут сильно деформироваться (сталь) или разрушаться, растрескиваться (природные камни, например, гранит), особенно при одновременном воздействии воды, применяемой при тушении пожаров. Трудносгораемые материалы под воздействием высоких температур тлеют и обугливаются, но при удалении огня процессы горения, тления или обугливания полностью прекращаются. К таким материалам относятся фибролит, гидроизол, асфальтовый бетон и др. Сгораемые материалы воспламеняются и горят или тлеют под воздействием огня или высокой температуры, причем горение или тление продолжается также после удаления источника огня. Среди них – древесина, войлок, битумы, смолы и др. Если источник высокой температуры (выше 1580°С) действует на материал в течение длительного периода времени (соприкосновение с печами, трубами, нагревательными котлами и т. п.), а материал сохраняет необходимые технические свойства и не размягчается, то его относят к огнеупорным. Огнеупорными являются шамот, динас, магнезитовый кирпич и другие материалы, применяемые для внутренней футеровки (облицовки) металлургических и промышленных печей. Материалы, способные длительное время выдерживать воздействие высоких температур (до 1000°С) без потери или только с частичной потерей прочности, относят к жаростойким, например, жаростойкий бетон, керамический кирпич, огнеупорные материалы и др. Температуростойкость или термостойкость — способность выдерживать чередование (циклы) резких тепловых изменений, нередко с переходом от высоких положительных к низким отрицательным температурам. Это свойство материала зависит от степени его однородности и способности каждого компонента к тепловым расширениям. Последняя характеризуется коэффициентом теплового расширения — линейным или объемным. Линейный коэффициент показывает удлинение 1 м материала при нагревании его на 1°С, а объемный характеризует увеличение объема 1 м3 материала при нагревании его на 1°С. Чем меньше эти коэффициенты и выше однородность материала, тем выше Температуростойкость, большее количество циклов резких смен температуры материал может выдержать без нарушения сплошности. Для цементного бетона линейный коэффициент теплового расширения равен (10—14) ∙10-6, для древесины вдоль волокон (3—5) ∙10-6, для стали (11—12) ∙10-6. Термическое расширение является упругим, и оно полностью обратимо. В основе возможного разрушения структуры лежат явления, под влиянием которых в материале возникают напряжения. Они возникают либо вследствие градиента температур, либо под влиянием изотропии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.018 с.) |


 (3.1)
(3.1)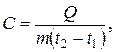 (3.2)
(3.2)


