
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет закрытой цилиндрической прямозубой передачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
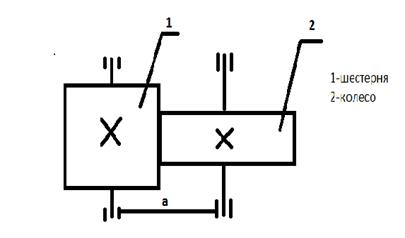
Схема передачи
Рисунок 2.1 - Схема закрытой цилиндрической прямозубой передачи
Задача расчета · Выбор материалов и вида термообработки зубчатых колес; · Определение геометрических параметров передачи; · Определение сил зацепления; · Выполнение проверочного расчета на контактную прочность и изгиб.
2.3. Данные для расчета: Таблица 2.1 – Силовые и кинематические параметры редуктора.
Условия расчета Надежная работа закрытой зубчатой передачи обеспечена при соблюдении условий прочности по контактным напряжениям и напряжениям изгиба. δH ≤ [δ]H δF ≤ [δ]F Допускается недогрузка передачи δH < [δ]H не более 10% и перегрузка δH > [δ]H до 5%.
Расчет зубчатой передачи В условиях индивидуального и мелкосерийного производства, предусмотренного техническим заданием на курсовую работу, в мало- и средненагруженных передачах, а также в открытых передачах применяют стальные зубчатые колеса с твердостью ≤ 350НВ. При этом обеспечивается нарезание зубьев после термообработки, высокая точность изготовления и хорошая прирабатываемость зубьев. Для увеличения нагрузочной способности передачи, уменьшения ее габаритов твердость шестерни НВ1 назначается больше твердости колеса НВ2: НВ1 = НВ2 + (20÷50)
2.5.1. Выбор материалов для изготовления зубчатых колес. Т.к. мощность Р<10 кВт, то выбираем для изготовления зубчатых колес редуктора стальные зубчатые колеса с твердостью ≤ 350НВ. Принимаем материал: для колеса - сталь 40Х, термообработка - улучшение, твердость сердцевины – 235НВ, твердость на поверхности – 261НВ. НВср=(235+261)/2=248; Для шестерни - сталь 40Х, термообработка - улучшение, твердость сердцевины – 268НВ, твердость на поверхности – 302НВ. НВср=(268+302)/2=285. НВ1=285>НВ2=248 на 37 единиц.
2.5.2. Определение допускаемого напряжения По таблице определяем величину [δ]H0 в зависимости от твердости: [δ]H0=1,8·НВср+67 Н/мм2 Т.к. проектируемый привод будет эксплуатироваться длительное время, принимаем коэффициент долговечности: КHL=1
Получаем [δ]H1 = КHL * [δ]H01 ср +67 =1*1,8*285+67 = 580 МПа [δ]H2 = КHL * [δ]H02 ср +67 =1*1,8*248+67 = 514 МПа В качестве расчетных принимаем: [δ]H = 0,45·([δ]H1+ [δ]H2) [δ]H = 0,45·(580+514)=493 МПа Допускаемое напряжение изгиба: [δ]F0=1,03·НВср [δ]F1 = КFL 1,03·НВср1 = 1,03*285 = 294 МПа [δ]F2 = КFL 1,03·НВср2 =1,03*248 = 256 МПа
2.5.3. Определяем межосевое расстояние редуктора:
где Кα = 49,5 МПа; ψва = 0,2; [δ]H =493 МПа По таблице Кнβ = 1; Т2=645Нм – крутящий момент на колесе.
Принимаем аω=250 мм.
2.5.4 Определяем нормальный модуль зацепления: mn = (0,01÷0,02)· аω mn = (0,01÷0,02)*250 mn = 2,5÷5 Принимаем стандартное значения модуля mn = 4 мм
2.5.5 Определяем число зубьев шестерни:
Z1= 2· аω/mn·(u+1) Z1= 2*250/4*3= 41 Принимаем Z1= 41, тогда Z2= Z1· u= 41*2= 82
2.5.6 Уточняем передаточное число: Uфак=Z2/Z1=82/41=2 Погрешность ∆ = (2-2)*100%/2= 0%
Рисунок 2. 2 - Геометрические параметры зубчатого зацепления 2.5.8 Определяем геометрические параметры шестерни и колеса:
Делительный диаметр: d= mn· Z d1= mn· Z1 = 4*41= 164 мм; d2= mn· Z2 = 4*82= 328 мм.
Диаметр окружности вершин зубьев: dа= d+2· mn d1= d1+2· mn = 164+2*4= 172 мм d2= d2+2· mn = 328+2*4= 336 мм;
Диаметр окружности впадин зубьев: df= d – 2,5·m df1= d1 – 2,5·m= 164 – 2,5*4= 154 мм df2= d2 – 2,5·m= 328 – 2,5*4= 318 мм;
Ширина венца: колеса: b2= ψва· аω b2= 0,2*250= 50 мм шестерни: b1= b2+ (5÷10) мм b1= 50+ (5÷10)= 55 мм;
Данные сводим в таблицу геометрических параметров передачи: Таблица 2.2 – Геометрические параметры зубчатого зацепления.
2.5.9 Определяем окружную скорость колес: υ= ω2· d2/2·103 υ= 77*328/2*103= 12,63 м/с Для данной скорости назначаем седьмую степень точности изготовления зубчатых колес. 2.5.10 Определение силовых параметров зацепления.
На рисунке 2.3 изображена схема сил в зацеплении цилиндрической прямозубой передачи.
Рисунок 2. 3 - Схема сил в зацеплении цилиндрической прямозубой передачи
В зацеплении прямозубых цилиндрических колес действуют силы: o Окружная Ft =2T1/d1 = 2*1000*183/164=2232 H o Радиальная Fr=Ft*tgα/cosβ=2232*0.364/1=812,5 Н
2.5.11 Проверочный расчет передачи по контактным напряжениям:
где Ft – окружная сила; KHα= 1,09; KHβ= 1; KHδ= 1,06; K=436;
δн= 436*√2232*4,66*1,09*1*1,06/328*50=373 Погрешность ∆= (373-493)*100%/493= -4,67% Недогрузка в пределах допустимой. 2.5.12 Проверочный расчет передачи по напряжениям изгиба: δF2= YF2·Yβ δF1= δF2· YF1/ YF2 ≤ [δ]F1 где KFα = 1,04; KFβ = 1; KFυ = 1,33; Yβ = 0,89; YF1 = 4,07; YF2 = 3,6.
Для шестерни Zv1=41/1=41;
Для колеса Zv2=82/1=82;
σF2 = 3,6*0,89*11,16*1,04*1*1,33=50 МПа;
σF1 = 50*4,07/3,6=57 МПа.
Условие (2.7) и (2.8) выполняются: 294 ≥ 57 256 ≥ 50 Заключение: результаты проверочных расчетов по контактным напряжениям и напряжениям изгиба показывают, что полученные геометрические параметры редуктора удовлетворяют заданным.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.54.61 (0.007 с.) |

 , (2.5)
, (2.5) ,
,
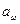 , мм
, мм

 ≤ [δ]H
≤ [δ]H KFα·KFβ·KFυ ≤ [δ]F2
KFα·KFβ·KFυ ≤ [δ]F2



