
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ротор вектора скорости и его физический смысл в вихревом сечении, теорема Стокса. Правила действий с оператором Гамильтона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ротор вектора скорости и его физический смысл в вихревом сечении, теорема Стокса. Правила действий с оператором Гамильтона.
Ротор представляет собой угловую скорость вращения твердого тела с точностью до числового множителя. Направление ротора – направление, вокруг которого циркуляция имеет наибольшее значение, по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S. Связь между ротором и циркуляцией аналогична связи между производной по направлению и градиентом. Циркуляция – это работа силы
Свойства ротора: 1) 2) 3) 4) Формулу Стокса можно записать в векторной форме:
Эта формула показывает, что циркуляция вектора Оператор Гамильтона служит для удобства записи основных операций над скалярным (
Символическое умножение вектора
Кризис течения в сжимаемых жидкостях. Запирание по расходу. Кризис течения – третье общее свойство сплошных сред, наряду с продольным расширением и поперечным сжатием частиц среды при ускорении. При кризисе течения межмолекулярные силы не способны удержать среду от резкого расширения.
В капельных жидкостях кризис течения приводит к кавитации, а в газах разрушение межмолекулярных связей приводит не только к еще б о льшему продольному расширению, но и к поперечному. Поэтому сверхкритическое ускорение газов требует расширяющегося канала. Статическое давление, при котором возникает кризис течения, зависит от рода газа, определяемого показателем адиабаты:
При достижении этого давление расстояние между молекулами становится критическим, а скорость становится равной местной скорости звука в данном сечении. При дальнейшем ускорении межмолекулярные силы начинают убывать обратно пропорционально квадрату расстояния между ними. Запирание канала по расходу – достижение предельного значения расхода для данного канала. При постоянном давлении перед сечением, попытка увеличить расход путем уменьшения давления за сечением приводит к увеличению интенсивности кавитации в капельных жидкостях. Для газов см. вопрос 28.
Работа, тепло и ускорение, вызванные силами вязкости. Примеры проявления составляющих вязкости, вихревой эффект. Вязкость – свойство сплошных сред оказывать сопротивление сдвигу двух слоев среды относительно друг друга. Сдвиг сопровождается только изменением формы, но не объема. Секундная работа сил вязкости, совершаемая массой газа внутри объема
Пренебрегая величинами второго порядка малости, окончательно работа вязкостных сил равна:
Для всех координатных осей:
Частные решения уравнения Навье-Стокса для ламинарного режима: течение Паузейля-Гагена, закон неквадратичного трения и коэффициент гидравлического трения для ламинарного режима течения. Участок гидродинамической стабилизации (начальный и разгонный). Коэффициент Кориолиса. Уравнение Навье-Стокса в общем виде: показывает, что вектор полного ускорения жидкой частицы равен векторной сумме ускорений, вызванных отдельными силами так, как будто бы каждая из этих сил действует на частицу в отдельности:
37. Уравнение количеств движения (первое уравнение Эйлера) в общем виде. Тензор импульса и его компоненты. Неконсервативная форма для расчета силового взаимодействия потока и обтекаемых тел.
Используется для расчета взаимодействия потока с обтекаемым телом. Выделим экспериментальную струйку тока: для неизменной массы:
После подстановки и интегрирования: Равнодействующая внешних сил, действующих в данный момент на жидкость равна изменению во времени суммарного количества движения и разности потоков количества движения жидкости на входе и выходе.
Кинематика движения жидкой частицы. Виды движения. Вихревое и потенциальное движение, условия незавихренности, потенциал скорости. Основные понятия. Уравнения, описывающие вихревое течение. Потенциальное течение – движение, при котором отсутствует движение частиц среды относительно собственных осей ( Вихревое течение – если ротор скорости или циркуляция скорости по любому замкнутому контуру отлична от нуля, то частицы вращаются вокруг собственных осей. Потенциал скорости – функция, частные производные которой соответствуют компонентам скорости: Ротор вектора скорости и его физический смысл в вихревом сечении, теорема Стокса. Правила действий с оператором Гамильтона.
Ротор представляет собой угловую скорость вращения твердого тела с точностью до числового множителя. Направление ротора – направление, вокруг которого циркуляция имеет наибольшее значение, по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S. Связь между ротором и циркуляцией аналогична связи между производной по направлению и градиентом. Циркуляция – это работа силы
Свойства ротора: 1) 2) 3) 4) Формулу Стокса можно записать в векторной форме:
Эта формула показывает, что циркуляция вектора Оператор Гамильтона служит для удобства записи основных операций над скалярным (
Символическое умножение вектора
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.11.230 (0.008 с.) |

 поля при перемещении материальной точки вдоль кривой
поля при перемещении материальной точки вдоль кривой  . Вдоль замкнутых векторных линий циркуляция не равна нулю, так как в каждой точке векторной линии скалярное произведение
. Вдоль замкнутых векторных линий циркуляция не равна нулю, так как в каждой точке векторной линии скалярное произведение 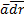 сохраняет знак, положительный при совпадении вектора
сохраняет знак, положительный при совпадении вектора  с направлением обхода векторной линии и отрицательной в обратном случае.
с направлением обхода векторной линии и отрицательной в обратном случае.

 , если
, если  постоянный вектор;
постоянный вектор;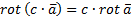 ,
,  ;
;



 , лежащую в поле вектора
, лежащую в поле вектора  ) или векторным (
) или векторным ( ,
,  ,
,  (векторные дифференциальные операции первого порядка). Он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями.
(векторные дифференциальные операции первого порядка). Он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями.
 на скаляр
на скаляр  на величины
на величины  как взятие соответствующей частной производной от этих величин.
как взятие соответствующей частной производной от этих величин.




 равна сумме произведений нормальных и касательных компонент вязкостных сил на скорость, в направлении которой действует та или иная компонента:
равна сумме произведений нормальных и касательных компонент вязкостных сил на скорость, в направлении которой действует та или иная компонента:





 , если масса меняется:
, если масса меняется:  . Прирост количества движения должен быть равен разности количеств движения для масс 2-2’ и 1-1’, которые в установившемся течении одинаковы.
. Прирост количества движения должен быть равен разности количеств движения для масс 2-2’ и 1-1’, которые в установившемся течении одинаковы.
 элементарная масса,
элементарная масса,  секундное количество движения.
секундное количество движения. уравнение Эйлера, силовая форма записи уравнения движения,
уравнение Эйлера, силовая форма записи уравнения движения,  сила реакции жидкости на обтекаемое тело.
сила реакции жидкости на обтекаемое тело.
 ).
). и т.д.
и т.д.


