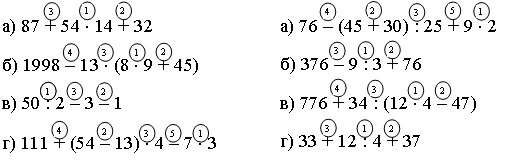Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление. Свойства деления (п. 12)Содержание книги
Поиск на нашем сайте
Урок № 44 Деление (п. 12) Цели: научить формулировать ответ на вопрос: «Какое действие называется делением?», повторить, как называются числа при делении, выработать навык деления натуральных чисел. Оборудование: на доске записать план изучения новой темы. Ход урока I. Устные упражнения. 1. Какой ряд быстрее сосчитает? (По количеству поднятых рук). № 493 (а, б). 2. № 497, 501 (вместо «подчеркнуть» употребите слово «назвать»). II. Изучение нового материала (идет по вопросам плана). 1. Определение действия деления. Решают задачу из текста и формулируют определение действия деления; читают несколько раз, 2–3 ученика формулируют это определение, и затем каждый своему соседу дает это определение. 2. Как называются числа при делении:
3. Что показывает частное? (Ответ сами ученики находят в учебнике). 4. Всегда ли возможно деление? В тетради ученики записывают: Ни одно число нельзя делить на нуль. 5. Свойство единицы и нуля при делении. а: 1 = а а: а = 1 0: а = 0. III. Закрепление. 1. Ученикам предлагается по учебнику найти ответы на вопросы плана. 2. № 473 (а–г) – комментирование с места. 3. Устно № 474 (а, б); 465; 467; 466. 4. № 472 (а, в, г, д, е, к). 5. Ответить на вопросы 1–4 к п. 12. IV. Итог урока. 1. Найти значение выражения: а) 285: с, если с = 1; с = 3; с = 19. б) d: 8, если d = 0; d = 96; d = 14. 2. Делимое в 14 раз больше частного. Можно ли найти делитель? 3. Каков правильный ответ? В равенстве (а – 37): (b +43) = 5 выражение (b + 43) является а)частным; б) делителем; в) делимым. IV. Домашнее задание: п. 12; № 517 (а, в); 518 (а, б), 515. Заполнить таблицу.
Урок № 45 Деление (п. 12) Цель: закрепить свойства деления. Оборудование: пленки к кодоскопу по проверке домашней работы. Ход урока I. Проверка домашней работы (пленка к кодоскопу). Учащиеся обменялись тетрадями и сверяют решения с экраном. II. Устные упражнения ( проверяют два ученика). 1. Продумайте, как проще выполнить умножение, и вычислите: а) 19 × 2 × 5; б) 4 × 27 × 25; в) 13 × 6 × 50. 2. Угадайте корни уравнения: 15 × а = 15: а. 3. Из данных выражений составьте верные равенства:
Можно соединить графами. 4. Вставьте вместо кружков знаки арифметических действий и при необходимости скобки так, чтобы равенства были верными. а) 100 o 8 o 6 = 52 б) 100 o 8 o 6 = 86 в) 100 o 8 o 6 = 98 III. Работа по теме урока. 1. Устно: № 474 (в, г); № 476; № 478 (а). 2. № 473 (д, е); 468, 469 (с комментированием). № 472 (б, з, и). 3. На повторение: № 499 (а); 500 (а); 506. IV. Итог урока. 1. Составьте выражения для решения задачи. а) Ракета пролетела за t мин 23380 км. С какой скоростью летела ракета? б) d: 8, если d = 0; d = 96; d = 14. 2. Ракета пролетела S км со скоростью 540 км/мин. Сколько минут летела ракета? V. Домашнее задание: п. 12; № 517 (б, г), 518 (в), 514, 520. Урок № 46 Цели: научить находить неизвестный множитель, делимое, делитель. Оборудование: девиз урока «Чем больше я знаю, тем больше умею»; плакаты на каждый этап устных упражнений. Ход урока I. Устные упражнения ( проводят ученики). 1. Первый ученик: «Отгадайте кроссворд».
По горизонтали: 1) Геометрическая фигура:
2) Символ, с помощью которого обозначают натуральные числа. 3) Инструмент для проведения отрезков. 4) Результат сложения. 5) Результат деления. По вертикали: 6) Знак одного из действий. 2. Второй ученик предлагает задание. Вычислить:
3. Третий ученик: «Отгадайте корень уравнения». а) z + z = z × z; б) 16: b = 16 × b. II. Работа по теме урока. 1. Устно № 475, 478 (б, в), 483. 2. Перед выполнением следующих заданий нужно задать вопросы: а) Какое равенство называется уравнением? б) Какое число называется корнем уравнения? в) Что значит решить уравнение? г) Как проверить, верно ли решено уравнение? 3. Решить: № 482 (а, б, г) – трое учеников одновременно решают у доски, затем класс проверяет их решение. № 485 (а, в); 487 (а). 4. На повторение: 499 (б), 501 (б). Можно соединить графами. III. Самостоятельная работа (по вариантам).
IV. Домашнее задание: п. 12 (2-я часть); № 524 (а, б, в), 516, 519, 527 (а, д). Урок № 47 Ход урока I. Проверка домашнего задания. Консультанты докладывают о выполнении домашнего задания. Отмечают аккуратно выполненные работы. II. Устные упражнения. 1. № 493 (д) (какой ряд быстрее сосчитает?). 2. № 495. 3. Вопросы по таблице домашнего задания. а) Во сколько раз скорость автомобиля «Волга» больше скорости почтового голубя? б) Во сколько раз скорость улитки меньше скорости пчелы? в) На сколько км/ч скорость автомобиля «Ока» больше скорости верблюда? III. Работа по теме урока. 1. № 464, 482 (б), 487 (в. г), 490, 488, 471 (а, б), 477, 486 (а, б). 2. На повторение: № 499 (в), 501, 502 (а, г). IV. Итог урока. 1. № 485 (б, г). 2. Повторить теоретический материал п. 12. V. Домашнее задание: п. 12; № 524 (г, д); 521, 523, 526 (а); 554 (б, е). Урок № 48 Деление (п. 12) Цели: вырабатывать навык деления натуральных чисел и применения свойств деления. Оборудование: плакат для логического теста. Ход урока I. Устные упражнения. 1. Среди чисел 10; 20; 0 найти корень уравнения: у × 10 = у: 10. 2. № 498. 3. Логический тест № 1. Анаграммой называется слово, в котором поменялись местами все или несколько букв в сравнении с исходным словом. Решить анаграмму – означает определить исходное слово. Учитель вывешивает плакат с анаграммами.
Ответ: 1) прямая, луч, отрезок, периметр. 2) Лишнее слово «периметр», так как «периметр» – метрическая величина, а «прямая», «луч», «отрезок» – геометрические фигуры. 4. Логический тест № 2 (символико-графического типа).
II. Работа по теме урока. 1. Устно № 491, 478. 2. № 492 (а) – с разбором, № 492 (б) – самостоятельно, № 472. 3. На повторение: № 502, 511. 4. Самостоятельная работа обучающего характера. (До начала урока пересадить учащихся так, чтобы в паре были «сильный» – «слабый»). № 472 (ж, л); 470; 487 (б, е); 479. III. Домашнее задание. п. 12; № 524 (е); 525; 522; 526 (б); 527 (в).
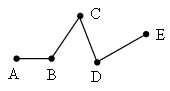
Урок № 49 Деление (п. 12) Что она красива». Петер Ропсе Оборудование: тексты задач на плакатах; ксерокопии листов с домашним заданием; плакаты с высказываниями о задачах; костюм для дяди Степы-милиционера. «Математическая задача иногда столь же увлекательна, как кроссворд, и напряженная умственная работа может быть столь же желанным упражнением, как стремительный теннис». Д. Пойа «Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!» Д. Пойа «При решении задачи плохой план часто оказывается полезным, он может вести к лучшему плану». Д. Пойа «В задачах, которые ставит перед нами жизнь экзаменатором является сама природа». У. Сойер Ход урока I. Устные упражнения. На доске записаны краткие условия задач. 1. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли автомобиль и велосипедист через 2 часа, если расстояние между пунктами 160 км? (Решить задачу двумя способами.) 2. Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 часа вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 часа после своего выхода? (Можно сделать чертеж к задаче.) II. Работа по теме урока. 1. Повторить, как найти расстояние, время, скорость, и решить задачи. 2. По рисунку составить задачу на движение и решить ее.
3. Викторина (3 ученика). а) Первый ученик: «Автомобиль «Москвич» за 3 часа может проехать 360 км. Бескрылая птица страус – лучший бегун в мире – развивает скорость до 120 км/ч. Сравните скорости автомобиля «Москвич» и страуса». б) Второй ученик предлагает классу свою задачу. «Скорость распространения света самая большая в природе – 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км? в) Третий ученик: «Пройденный путь пешехода S, его скорость u и время движения t связаны соотношением S = ut. Если пешеход за 4 часа прошел 24 км, то его скорость равна: 1) 12 км/ч; 2) 6 км/ч; 3) 96 км/ч; 4) 8 км/ч. 4. Решить олимпиадную задачу. Из пунктов А и В, расстояние между которыми 100 км, со скоростями 20 км/ч и 30 км/ч выезжают навстречу друг другу два велосипедиста. Вместе с ними со скоростью 50 км/ч вылетают две мухи, летят до встречи, поворачивают и летят обратно до встречи с велосипедистами, снова поворачивают и т. д. Сколько километров пролетит каждая муха в направлении от А до В до того момента, когда велосипедисты встретятся? Решение: Велосипедисты встретятся через 2 часа на расстоянии 40 км/ч от А. За это время каждая муха пролетела 100 км. Муха, вылетевшая из А, пролетела в направлении от А до В на 40 км больше, чем в обратном направлении, и поэтому от АВ она пролетела 70 км. Аналогично, вторая муха в направлении от А к В пролетела на 60 км меньше, чем в обратном, то есть 20 км. Ответ: первая муха в направлении от А к В пролетела 70 км, вторая – 20 км. 5. Входит дядя Степа-милиционер и предлагает задачу из сборника задач по основам безопасности дорожного движения. а) Ширина проезжей части дороги 15 м, зеленый сигнал светофора горит 20 секунд. С какой наименьшей скоростью может двигаться пешеход с момента загорания светофора, чтобы благополучно перейти дорогу? Решение: 1) 15 м = 1500 см 2) 1500: 20 = 75 см/с. Ответ: пешеход может двигаться со скоростью 75 см/с. б) Мотоциклист едет со скоростью 95 км/ч, а скорость велосипедиста на 76 км/ч меньше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Кому из них легче остановиться? Решение: 1) 95 – 76 = 19 км/ч 2) 95: 19 = 5 раз. Ответ: в 5 раз легче остановиться велосипедисту, так как при меньшей скорости короче тормозной путь. III. Итог урока. Отметить особо отличившихся учеников, если есть возможность, то наградить сувенирами. VI. Домашнее задание: ученикам раздаются ксерокопии заданий. 1) Помогите французским девочкам. Однажды Жанин и Моника поплыли по маленькой речке, отправившись из одного и того же места, но только Жанин поплыла против течения, а Моника поплыла по течению. Оказалось, что Моника забыла снять большие деревянные бусы. Через четверть часа девочки повернули обратно. Кто же из них подберет бусы Моники: сама Моника или Жанин? (Скорость обеих пловчих в неподвижной воде одинакова.) 2) Задача от дяди Степы. Скорость легкового автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько раз скорость легкового автомобиля больше скорости грузовика? Какой автомобиль опаснее для школьника, начавшего движение по пешеходному переходу?
3) Задание от «Знающего человека». Заполнить таблицу.
4) Составить по одной анаграмме. Ответы для учителя. Задача № 1 Скорости девушек относительно неподвижной воды одинакова. Но ведь по отношению к воде в реке бусы остаются неподвижными – они движутся в точности с такой же скоростью, что и вода (со скоростью течения). Пловчихи проплывают относительно воды одинаковое расстояние и по истечении получаса встречаются в том месте, где в этот момент находятся бусы. Таким образом, обе девушки могут подобрать бусы с равным основанием, так как встречаются в тот самый момент, когда подплывут бусы. Задача № 2 Опаснее легковой автомобиль, так как у него скорость больше, кроме того, для водителя легкового автомобиля мальчик появится неожиданно, так как обзор будет закрыт грузовым автомобилем.
Урок № 50 Деление с остатком (п. 13) Цели: объяснить учащимся, что деление натурального числа на другое нацело не всегда возможно; научить называть компоненты при делении с остатком и выполнять деление. Оборудование: пленка для устных упражнений; кодоскоп. Ход урока I. Устные упражнения. 1. № 540 (а, б, в), 541 (а, б) – просвечивается на экран. 2. Учащиеся из своего домашнего задания задают анаграммы классу. III. Закрепление. 1. Ответить на вопросы п. 13. 2. № 533 (д, б, в), 533 (а, е), 532 (3-я строка); 538. 3. На повторение. № 548 (3, 4) – самостоятельно. IV. Итог урока. Тест 1) При делении числа на 46 может получиться остаток: а) 48; б) 45; в) 46; г) 47. 2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза; г) на 15 км/ч. 3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза. V. Домашнее задание: п. 13 (уметь пересказать конспект); № 550 (а, в); 552; 553 (а); 555 (а, г), повторить п. 12.
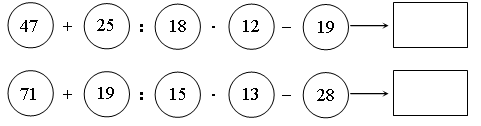
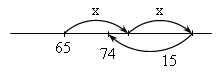
Урок № 51 Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления. Оборудование: билеты для проверки домашнего задания; плакат для устных упражнений и итогового теста; билеты с дополнительными вопросами. Ход урока I. Сообщается тема урока и цель, которая стоит перед учащимися. 10 человек вызываются к доске. Каждый из них вытаскивает себе билет. Пока класс выполняет устные упражнения, ученики готовятся к ответу, а потом отвечают. Устные упражнения. 6 человек за первыми партами, 4 человека у доски обдумывают ответ на свои билеты. 1. Вывешивается плакат: «Восстановите цепочку вычислений».
2. Кто быстрее сосчитает? 60 – 22 : 2 + 64 3. № 540 (д), 542. Задания на билетах:
III. Итог урока. 1. Придумать задачу, используя равенство: 2891 = 2 × 1000 + 891. 2. Тест (с международного конкурса «Кенгуру»). Вывешивается плакат. Вдали мы видим силуэты замка. Какая из следующих линий не является частью этого силуэта?
III. Домашнее задание: п. 13, повторить п. 12; № 550 (б, г); 553 (б); 555 (в, г); 556 (а).
Урок № 52 Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления. Оборудование: плакат на доске к № 526 (б). Ход урока I. Устные упражнения. Одновременно трое учеников с текстами домашних заданий решают у доски. По окончании выполнения устных упражнений класс сверяет домашнее задание с доской.
Ход урока III. Итог работы. Чтобы учителю получить информацию о КПД урока, предложить учащимся письменно (на листочках) сформулировать свойство умножения и листочки потом собрать. IV. Домашнее задание: п. 14 (1-я часть); № 609 (а), 610 (а, в), 611 (а, в), 625 (а).
Урок № 55 Цели: научить применять свойства умножения при упрощении выражений. Оборудование: плакат или пленка для кодоскопа (№ 577, 578). Ход урока I. Проверка домашнего задания. Консультант докладывает о результатах выполнения домашнего задания; к тем номерам, которые вызвали затруднение у многих, дается пояснение. II. Устные упражнения. 1. Повторение теоретического материала п. 14 (1-я часть). 2. № 590 (в, г), 591 (а). 3. На доске написать большую цифру «0». Учитель: Что вы, ребята, об этом числе и цифре знаете? При сложении каких чисел может получиться «0»? В каких случаях получается нуль при вычитании, при умножении, при делении? IV. Закрепление. 1. Каким свойством умножения воспользуемся при выполнении № 559? Устно: № 559 (ж, з), 564, 575 (а, б). 2. № 561 (а, б), 560 (д, е) – Чем отличаются задания этих номеров? в) 550 (б, д, в, ж) – комментирование с места. 3. Вызываются 4 человека к доске. 1) № 568 (а); б) № 568 (в); в) № 568 (д); г) № 576 (а). 4. № 577 (решить уравнением и арифметически). 5. На повторение № 603, 601 (г, е) – самостоятельно. V. Итог урока. Тест 1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках? а) х; б) 2х; в) 3х; г) 4х. 2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе? а) 4а; б) 6а; в) 2а + 4; г) а +4. 3) Даны два выражения: 9(856 + 342) и 9 × 856 + 8 × 342. Какое выражение больше? а) равны; б) первое; в) второе. VI. Домашнее задание. п. 14; № 609 (б, г); № 614 (а, б); 612, 613 (б, г); 625 (б). Повторить п. 11–13. Придумать частушки про «нуль». Вопросы из п. 11–14.
Урок № 56 Упрощение выражений (п. 14) Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений. Оборудование: ксерокопии к домашнему заданию. Ход урока I. Проверка домашнего задания (решение записано заранее). Соседи по парте обмениваются тетрадями, сверяют решение с доской. II. Устные упражнения. 591 (б, в); 592 (в, г); 572 (б, г). IV. Итог урока. «Математическая перестрелка». Выбирается жюри из 3–5 человек. Класс делится на две команды. 1) Конкурс частушек про «нуль» (было задано на дом). 2) Команды друг другу задают вопросы по п. 11–14, примеры для устного выполнения. Те, кто не смог ответить на вопрос, выбывают из игры. Жюри подводит итоги. V. Домашнее задание. п. 14. Заполнить таблицу (даются ксерокопии), № 614 (в, г); 616; 623; 625 (в). Образец таблицы
Урок № 57 Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений. Оборудование: карточки для устных упражнений. Ход урока I. Проверка домашнего задания. 1. Сверить с доской решение задачи № 623. II. Устные упражнения. № 593 (а. б); 594 (а), 600. Каждому ученику дается карточка, в которой нужно записать только ответ.
Ход урока I. Проверка домашнего задания. 1. Задача № 621 (сравнить решение с доской). 2. Вопросы к п. 1, 2. Прочитать числа. II. Устные упражнения. 1. № 590 (д); 593 (в); 594 (б). 2. Повторить свойства умножения. III. Работа по теме урока. 1. № 567 (а, б); 567 (б, д); 572, 574 (г). 2. Самостоятельная работа.
IV. Итог урока. 1) Дать пояснение к задаче № 615. 2) Отгадать чайнворд (№ 625). V. Домашнее задание. п. 14, повторить п. 3, 4; № 622, 617, 625 (г).
Урок № 59 Цели: научить различать действия первой ступени и действия второй ступени, правильно выполнять порядок действий. Оборудование: плакат для устного счета, магниты; плакат для развития внимания и памяти. Ход урока I. Устные упражнения. 1. Восстановить цепочку вычислений.
2. Вычислить устно: 15 × 4 25 × 3 +16 : 15 : 19 +29 –4 : 17 ? ? 3. Упростите выражение: а) 2а + 612 + 7а + 324 б) 38 + 5а + 75 + 6а. III. Закрепление. 1. Повторить теоретический материал по вопросам п. 15. 2. Решить у доски: а) № 627 (а); б) 627 (в); в) 627 (д); г) 627 (и). а) № 628 (а); б) 628 (г); в) 628 (д); г) 628 (в). 3. Самостоятельная работа обучающего характера. № 627 (е, з); 639 (а, д, ж); 642. IV. Итог урока. Тренировка внимания. Учитель показывает ребятам плакат и обращается к ним: «Внимательно посмотрите на плакат. Вам дается 1 секунда, после чего плакат будет убран, а вы должны сложить три числа, которые были на нем, и назвать сумму этих чисел».
Эксперимент заключается в том, что дана установка: назвать сумму трех чисел. А вопросы будут иметь другое содержание: какое число записано внутри квадрата, треугольника и круга. V. Домашнее задание. п. 15 (до программ и команд); № 647 (а, б, ж, з), 648 (б, г), 650.
Урок № 60 Ход урока I. Проверка домашнего задания. Выполнить тест. В выражении 200 + (20 –10: 2) × 8 последним выполняется действие: а) умножение; б) деление; в) вычитание; г) сложение. | 1) В выражении 400 – (40 + 2 × 7): 2 последним выполняется действие: а) умножение; б) сложение; в) деление; г) вычитание | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
В выражении 19 × 57 – 69 + 120: 5 последним выполняется действие: а) сложение; б) вычитание; в) деление; г) умножение. | 2) В выражении 740 – 600: 15 + 7 × 33 последним выполняется действие: а) умножение; б) деление; в) вычитание; г) сложение. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3) Составьте выражение для решения задачи: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| В классе 25 человек. После уроков 7 человек пошли домой, а остальные разбились поровну на три команды для игры. Сколько человек в каждой команде? а) 25: 3 – 7; б) 25 – 7: 3; в) (25 –7): 3; г) (25 – 3): 7. | У Белоснежки и 7 гномов было 25 конфет. Белоснежка съела 4 конфеты, а остальные конфеты гномы разделили между собой поровну. Сколько конфет стало у каждого гнома? а) (25 – 4): 7; б) (25 – 7): 4 в) 25 – 4: 7; г) 25: 7 – 4. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4) Не производя вычислений определите, в каком из примеров указанный порядок действий приводит к неверному результату:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица для заполнения.
| Фамилия, имя___________________класс______ | Оценка учителя | ||||
| Номер задания | 1 | 2 | 3 | 4 |
|
| Правильный ответ | |||||
Калька прикрепляется к таблице скрепками, ученики пишут ответ на кальке, через кальку хорошо видна таблица. После проверки работы ученика скрепки удаляются, калька с записями открепляется от карточки и с выставленной оценкой возвращается ученику.
II. Устные упражнения.
1. Восстановите цепочку вычислений:

2. Кто быстрее сосчитает?
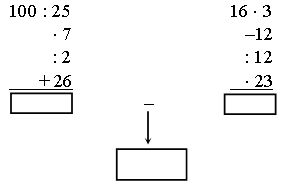
3. № 638 (а, в).
V. Итог урока.
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140: 4 + 3) × 5; б) 140: (4 + 3 × 5); в) 140: (4 + 3) × 5.
2) Дано выражение 157 × 18 – 57 × 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 × 57; б) 158 × 18 – 57; в) 18 × (157 – 57).
VI. Домашнее задание: п. 15; № 632, 631, 634 (а, в). Составить числовое выражение из 4 действий и схему к нему.
Урок № 61
Ход урока
I. Самостоятельная работа.
| I вариант | II вариант |
| 1) Выполните вычисления по схеме. Запишите выражение со скобками, соответствующее вычислительной схеме. | |

| 
|
| 2) Составьте программу вычисления выражения: | |
| (75 × 234 + 27 × 53) × 2 | (67 × 42 – 73 × 21): 3 |
Запишите эту программу в виде схемы. Найдите значение выражения.
II. Устные упражнения.
№ 634 (д), 635, 637, 638 (б, г).
III. Работа по теме урока.
1. Что такое команда? (Последовательность выполнения действий в выражении). № 630 (ниже дан образец выполнения).
Числовое выражение: 381 × 29 – 7248: 24.
Программа вычислений:
1) Умножить 381 на 29.
2) Разделить 7248 на 24.
3) От результата выполнения команды 1 отнять результат выполнения команды 2.
Схема выполнения.

2. № 632 (б).
3. Записать числовые выражения: № 646, 645 (домашние упражнения).
4. Выполнить № 627 (ж, к).
5. Самостоятельная работа по вариантам.
Вариант I: № 627 (л); 643 (1).
Вариант II: № 627 (м); 643 (2).
IV. Итог урока.
1. Ответить на вопросы к п. 15.
2. Соревнование соседей по парте: № 651.
V. Домашнее задание. п. 15 повторить 5, 6; № 644, 647 (в, г, д, е), 649. Составьте числовое выражение из 4 действий и схему к нему.
Урок № 62
Квадрат и куб числа (п. 16)
Цели: научить формулировать определение квадрата и куба числа, возводить числа в квадрат и куб, находить значения числовых выражений, содержащих вторую и третью степень натурального числа.
Оборудование: план изучения темы; плакаты для устных упражнений.
Ход урока
II. Закрепление.
1. № 655, 652 (составить таблицу и выучить).
2. № 657 (а, г, и).
3. Самостоятельно: № 657 (б, в).
4. На повторение: № 663. Девочки – № 665 (1), мальчики № 665 (2).
III. Устные упражнения.
1. 23 – 4; 2) 52 + 22; 3) 152 – 25.
2. Каков порядок действий: а) 160 + 37 – 20 + 52.
б) 90 – 60: 15.
3. «Быстро сообрази».
Найдите математический термин из четырех букв, который служит окончанием слов:
Пери…, диа…, мано…
IV. Домашнее задание. п. 16; № 666, 671, 669, 673. Выучить таблицу квадратов (от 1 до 20) и кубов (от 1 до 7), повторить п. 7, 8.
*Поставить скобки так, чтобы равенство было верным:
9664: 32 – 2 × 195 – 37 × 5 = 3000.
Урок № 63
Квадрат и куб числа (п. 16)
Цели: выработать навык в вычислении значения выражения, содержащего квадрат и куб числа.
Оборудование: карточки, таблицы, калька для выполнения теста; набор карточек с числами от 1 до 20.
Ход урока
I. Выполнить тест.
| I вариант | II вариант |
| 1) Вычислите: | |
| 82 а) 64; б) 16; в) 2; г) 8. | 103 а) 30; б) 3; в) 10; г) 1000. |
| 2) Вычислите: | |
| 2 × 43 а) 24; б) 128; в) 512; г) 32. | 3 × 52 а) 45; б) 30; в) 225; г) 75. |
| 3) Упростите выражение: | |
| 11а – а – 21 | 11у + у + 3 |
| а) 11а –2; б) 8а; в) 3а; в) 10 а – 2 | а) 11у + 3; б) 12у + 3; в) 14у; г) 15у. |
| 4) Найдите значение выражения: | |
| у3 – 2 при у = 6. а) 16; б) 216; в) 214; д) 64. | х2 + 5 при х = 11 а) 126; б) 121; в) 27; г) 256. |
| 5) Упростите выражение: | |
| 19 –(14 + с) а) 5с; б) 5 + с; в) 33 – с; г) 5 – с. | 15 – (b + 2) а) 17 – b; б) 13 – b; в) 13b; г) 13 + b. |
| 6) Для того чтобы разность 2874 945 1*2* была верной, вместо * надо поставить цифру: а) 9; б) 1; в) 0; г) 3. | 6) Для того чтобы разность 3284 648 2*2* была верной, вместо * надо поставить цифру: а) 3; б) 7; в) 6; г) 4. |
Таблица (с калькой) для заполнения результатов
| Фамилия, имя _________________________класс_____ | Оценка учителя | ||||||
| Номер задания | 1 | 2 | 3 | 4 | 5 | 6 |
|
| Ответ | |||||||
II. Устные упражнения.
1. № 660 (а, в), 659 (г, д), 661.
2. Учитель показывает карточку и говорит «квадрат», ученики называют квадрат этого числа; аналогично повторяют кубы чисел.
3. Самостоятельно: № 657 (б, в).
4. На повторение: № 663. Девочки – № 665 (1), мальчики № 665 (2).
III. Тренировочные упражнения:
1. № 657 (д, з, е, ж), 658.
2. На повторение: № 664, 665 (з, и).
а) Вычислите (43 – 72) × 84.
б) В каких случаях квадрат числа с равен частному с: с?
в) Вычислить устно и записать только ответ.
138 + 189 – 118 245 × 25 × 8
243 + 589 – 489 38 × 37 + 63 × 38
IV. Домашнее задание. п. 14–16; № 668,670, 672. Таблицы квадратов и кубов. Прочитать с. 117. Подготовиться к контрольной работе.
Урок № 64
Контрольная работа № 5
| I вариант | II вариант | ||
| 1) Найдите значение выражения: | |||
| а) (1142600 – 890778): 74 + + 309 × 708. б) 132 + (52 – 49)3 | а) 508 × 609 – (223136 + 18916): 69 б) (44 – 38)2 + 132 | ||
| 2) Решите уравнение: | |||
| а) 4а + 8а = 204 б) 12у – 7у = 315 | а) 5m + 6m = 231 б) 7х – 3х = 412 | ||
| 3) Решите задачу: | |||
| В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке? | В двух ящиках 75 кг яблок. В первом ящике в 2 раза больше яблок, чем во втором. Сколько яблок во втором ящике? | ||
| 4) Упростите выражение | |||
| 147 + 23х + 39х и найдите его значение при х = 3 и при х = 10 | 67х + 133 + 27х и найдите его значение при х = 4 и при х = 10 | ||
| 5) У Коли несколько трехкопеечных и несколько пятикопеечных монет. Всего 80 копеек. Трехкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трехкопеечных монет у Коли? | 5) У
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.210 (0.011 с.) |
|||