
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлены и операции над нимиСодержание книги
Поиск на нашем сайте
Одночлен или моном – простое математическое выражение, прежде всего рассматриваемое и используемое в элементарной алгебре, а именно, произведение, состоящие из числового множителя и одной или нескольких переменных, взятых каждая в неотрицательной степени. Одночленом также является каждое отдельное число, причем степень такого одночлена равна нулю. Многочлен или полином от n переменных от
С помощью многочлена вводятся понятия «алгебраическое уравнение» и «алгебраическая функция». Полной степенью одночлена называется целое число следующего вида
Множество мультииндексов I, для которых коэффициенты Коэффициенты многочлена обычно берутся из определенного коммутативного кольца R. Иными словами, для операций сложения и умножения многочлены образуют кольцо, которое обозначается 1. Составляется сумма или разность исходных многочленов, для чего многочлены заключаются в скобки и между этими скобками ставятся знаки сложения или вычитания; 2. Скобки раскрываются; 3. Приведение к стандартному виду (приведение подобных). Умножение многочлена на многочлен базируется на распределительном свойстве умножения и сводит умножение многочленов к умножению друг на друга всех составляющих их членов – умножению одночленов. Чтобы умножить на каждый член второго многочлена и сложить полученные произведения. На основании умножения многочленов вводится действие возведения многочлена в степень, которое заключается в умножении многочлена на само себя столько раз, сколько указывает показатель степени. Деление многочлена на многочлен существенно отличается от всех вышеуказанных действий и в общем случае результатом выполнения действия не является многочленом. В частных случаях результатом деления двух многочленов является многочлен. Многочлен
Теорема: Любой многочлен
Деление многочлена на многочлен удобно выполнять уголком по аналогии с обычными действительными числами. Пусть A – алгебра над кольцом R, тогда произвольный многочлен
Многомерное интегрирование Пусть
Исходя из этого получаем соотношение
Данное соотношение основано на следующем равенстве
Исходя из этого, порядок интегрирования повторного интеграла не имеет значения. Двойной интеграл от функции двух переменных
Двойной интеграл определяет площадь под поверхностью
Аналогично вводится и тройной интеграл, который определяет объем тела, ограниченного поверхностями. Вычисление двойных и тройных интегралов производится следующим образом: сначала интеграл сводится к повторному, затем каждый интеграл вычисляется справа на лево с учетом техник и свойств интегралов.
Основы теории графов Графом называется совокупность множества его вершин
Если имеются две встречных дуги Граф можно представить в виде отношения Помимо рассмотренных имеются другие способы задания графа. Матрица смежностей является квадратной Матрица инцидентности имеет строк в количестве m – количество дуг графа, число столбцов n – число вершин графа, в каждой строке элемент – 1, в столбце с начальной вершиной и элемент 1 с конечной вершиной дуги. В остальных случаях - 0. Список смежностей – из двух столбцов с числом строк m – число дуг, где в каждой строке первое число дает номер начальной вершины, второе число – конечная вершина дуги. Граф Можно неэквивалентность графов доказать, получив для одного графа такой подграф, который не является подграфом для другого. Таким образом можно проверить, будут ли два рисунка изображать один граф в случае эквивалентности либо разные графы в случае неэквивалентности. Маршрут графа называют простым, если он не содержит циклов. Маршрут является циклом, если его начальные и конечные вершины совпадают. Вершина Граф называют двусвязным, если его вершины разбиваются на два непересекающихся множества, которые с сохранением связи образуют связные подмножества с отсутствием связи между их подмножествами. Аналогично задается n-связный граф. Теорема: Для неориентированного графа число вершин с нечетным порядком всегда является нечетным. Теорема Эйлера: В неориентированном графе существует цикл или маршрут Эйлера, если среди порядков вершин только два нечетных числа. Цикл Эйлера содержит единожды каждое ребро графа при совпадении начальной и конечной вершины, если порядки всех вершин графа четные. Маршрут Эйлера – маршрут, проходящий единожды по каждому ребру графа. Граф называется плоским, если он на плоскости изображен без пересечения ребер. Планарным является граф, который эквивалентен с некоторым плоским графом, иными словами, его можно изобразить на плоскости без пересечения ребер.
Два графа являются гомеоморфными, если можно один из них получить из другого конечным количеством добавлений и исключений вершин кратности 2. Теорема: Граф G является планарным, если он не содержит подграфов гомеоморфных Всякий граф, который можно уложить на плоскости, можно уложить и на сфере без пересечения ребер. Справедливо и обратное. Граф, который укладывается на сфере без пересечений является планарным. Многогранник является выпуклым, если для любой плоскости, проходящей по одной из его граней, точки тела лежат по одну сторону от этой плоскости. Теорема Эйлера о многогранниках: Для любого выпуклого многогранника выполнено: число вершин + число граней – число ребер = 2. Если многогранник является k-связным, тогда число вершин + число граней – число ребер = k + 1. Всякий выпуклый многогранник можно уложить на сфере. Для этого достаточно центр сферы взять внутри него, радиус взять так, чтобы многогранник оказался внутри и выполнить проекцию вершин на сферу. Всякий многогранник можно рассматривать в виде графа, который является его каркасом, тогда выпуклый многогранник дает планарный граф, который можно уложить не только на сфере, но и на плоскости без пересечения ребер. Для непланарных графов можно подобрать более сложные поверхности. Например, граф Если на графе введем понятие грани в виде цикла, внутри которого можно провести замкнутую линию, тогда получим новую теорему о планарности графа. Теорема: Односвязный граф является планарным, если число вершин + число граней – число ребер = 2; для k-связного графа число вершин + число граней – число ребер = k + 1. Граф G является планарным, если граф не содержит подграф, который стягивается к графу Деревом называется связный граф без циклов. Пусть дан граф, в котором некоторые две вершины можно соединить различными маршрутами, тогда возможно удалить хотя бы одно ребро графа, не нарушая его связность. Полученный на последнем шаге граф, удаление ребра, в котором нарушает его связность, называется каркасом. Полученный граф является деревом, в нем любые две вершины соединяет единственный маршрут. По построению каркаса можно определить количество ребер в графе: если имеется n вершин, тогда для дерева будет
Методы оптимизации При технологическом пути развития человек старается определить минимальные затраты для получения большей прибыли. Математически это сводится к максимизации или минимизации некоторой величины с учетом ограничения влияющих на нее факторов или параметров. Количество оптимизирующей величины или меру описывает значение функции, переменными для которой являются несколько факторов или параметров в числовом выражении Связь между переменными и ограничения на их значения задаются уравнениями или неравенствами, совокупность которых образует систему ограничений следующего вида
Система ограничений в пространстве переменных задает допустимую область значений. Задача оптимизации заключается в том, чтобы найти Непрерывный метод оптимизации функции нескольких переменных заключается в том, что в соответствии с системой ограничений исследуется область допустимых значений D. Если такая область пустая, тогда задача не имеет решения. Если точка единственная, тогда она является решением задачи. При конечном количестве точек достаточно для каждой найти значение функции и выбрать максимальное и минимальное значения. Если область D имеет нечетное количество точек, обладая при
Для критических точек внутри области D проверяем наличие гладкого безусловного экстремума, в которых второй дифференциал должен иметь постоянный знак. Решение задачи оптимизации гарантированно, если функция непрерывна и область D ограничена или замкнута. Неограниченность области может привести к недостижимости оптимального решения. Область D является замкнутой, если содержит все граничные точки и исключение точки границы может привести к недостижимости оптимального решения. Если область D задается функционально в виде
Подставив функцию из
Из данное системы получим координаты условного экстремума. Если учитывается несколько ограничений, тогда в левую часть добавляется множитель Пусть в плоскости Значение целевой функции во внутренних точках безусловного экстремума на каждом участке границы и в угловых точках области, где пересекаются несколько границ, вычисляем и среди них находим максимум или минимум функции с указанием значений соответствующих переменных. Если оптимизируется линейная n-мерная функция при линейных ограничениях, тогда такая задача оптимизации называется задачей линейного программирования. Канонический вид задачи линейного программирования содержит только неравенство с не отрицательностью некоторых или нескольких переменных. При В графическом методе решения задачи линейного программирования после построения области допустимых значений строится вектор Пусть основная задача линейного программирования состоит в максимизации линейной функции при некоторых ограничениях с не отрицательностью некоторых элементов. Всякому виду основной задачи всегда сопоставляется двойственная задача линейного программирования. Двойственная задача получается транспонированием матрицы коэффициентов целевой функции и ограничений, при этом стремление целевой функции меняется на противоположное и виды ограничений меняются на противоположные, за исключением равенств. Теорема: Если X - допустимое решение основной задачи и Y - допустимое решение двойственной задачи, тогда Теорема: Если одна задача из двойственной пары имеет единственное оптимальное решение, тогда и другая также имеет единственное оптимальное решение. Теорема: Если основная задача имеет единственное оптимальное Аналогично задаче линейного программирования задается задача параметрического программирования. При этом целевая функция имеет коэффициенты, зависящие от параметра t. Основная задача параметрического программирования вместе со своей двойственной задачей образуют задачу линейного программирования. Пусть в двумерном массиве Если Y имеет параметры
Упрощенная версия этой функции имеет вид метода наименьших квадратов
Исходя из условий экстремума этой функции получим оптимальный набор параметров. В данном случае оптимальными параметрами являются минимальными значениями для часто встречающихся функций одной переменной. Для двумерного массива точек подберем прямую вида
Условие экстремума в данном случае условие экстремума примет вид
Решение данной системы дает оптимальные параметры прямой по методу наименьших квадратов – линейный регрессионный анализ
Граф можно оптимизировать различными способами и опираясь на разные параметры. Взвешенный граф, на котором указаны начальные и конечные вершины называют сетью. Используя алгоритм Форда-Беллмана, можно найти маршрут в сети с минимальным общим весом. На начальном этапе каждой вершине сети присваивается условный неопределенный вес. Для начальной вершины условный вес равен нулю, для смежных с ней вершин условный вес заменяется на вес ведущей дуги. Обследованные вершины включаются в список достижимых из начальной вершины. Последним шагом находят смежные вершины и заменяют условный вес суммой весов дуг. Если ведущая в вершину дуга не дает уменьшения условного веса ее конечной вершины, тогда эту неотрицательную дугу исключают из рассмотрения. Процесс рассмотрения до тех пор, пока не будут рассмотрены все вершины списка и список вершин и весов перестанет изменяться. В результате получим аналог каркаса, по которому из начальной вершины можно оптимально добраться в каждую вершину графа. Общий вес маршрута будет оптимален. Вес конечной вершины даст минимальный общий вес маршрута. Такая задача относится к задачам динамического программирования. Пусть имеется некоторый проект, который состоит из нескольких отдельных операций. Для анализа такого проекта используют граф со схемами: вершина – операция и соединяющие их дуги показывают последовательность выполнения этих операций или дуга – операция, где соединения вершин графа дают моменты для начала и завершения, без которого не может начаться следующая операция. Кроме последовательного соединения таких вершин, возможны параллельно изображаемые участки, которые не связаны между собой и могут выполняться одновременно. Общее время выполнения операций – общее максимальное время маршрута от начальной до конечной точки – критический маршрут. Уменьшение весов не участвующих в этом критическом маршруте – время выполнения других процессов не позволяет на общее время выполнения других процессов.
Основы теории игр Под игрой в математике понимают конфликтную ситуацию с участием нескольких сторон – игроков. В коалиционных играх цели игроков полностью или частично совпадает. В игре с нулевой суммой суммарный проигрыш одних игроков и суммарный выигрыш остальных точно совпадают. Каждые из сложившихся ситуаций в игре описывается правилами, по которым устанавливается либо ничейный результат, либо выигрыш одного или нескольких игроков. Парная аналитическая игра называется матричной, если ее правила задаются матрицей платежей одного из игроков, где положительный платеж – выигрыш, а отрицательный платеж – проигрыш. Если выигрыш получается из ставок противников, тогда чистые выигрыши игроков могут быть другими. Для первого игрока по каждой строке платежей матрицы A найдется минимальное значение, из которых найдем наибольшее значение Если верхняя и нижняя цены равны, тогда игра имеет седловую точку, иными словами, строка Пусть матричная игра составлена матрицей платежей
Элементы векторов – числа от 0 до 1 – доля приемлемых возможностей в большой серии игр. Смешанная стратегия игрока является оптимальной, если ее применение в большой серии игр приводит к максимально возможному большему выигрышу и среднему выигрышу равному
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.19 (0.015 с.) |

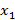 до
до 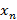 – сумма одночленов или строго конечная сумма следующего вида, в котором
– сумма одночленов или строго конечная сумма следующего вида, в котором 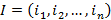 – набор из n целых чисел, именуемый мультииндексом;
– набор из n целых чисел, именуемый мультииндексом; 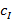 – число, именуемое коэффициентом многочлена, зависящее только от мутииндекса I.
– число, именуемое коэффициентом многочлена, зависящее только от мутииндекса I.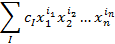

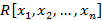 . Сложение и вычитание многочленов происходит по следующему принципу:
. Сложение и вычитание многочленов происходит по следующему принципу: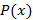 делится без остатка на многочлен
делится без остатка на многочлен 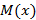 , если существует многочлен
, если существует многочлен 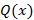 такой, что справедливо следующее соотношение
такой, что справедливо следующее соотношение 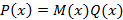 .
.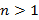 можно представить в виде
можно представить в виде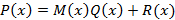 , где
, где 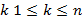 ;
; 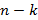 и
и 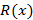 – многочлен, степень которого меньше k, причем такое представление единственно.
– многочлен, степень которого меньше k, причем такое представление единственно.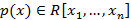 определяет полиномиальную функцию
определяет полиномиальную функцию 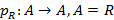 . В случае, если R – поле вещественных или комплексных чисел, тогда функция
. В случае, если R – поле вещественных или комплексных чисел, тогда функция 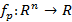 полностью определит многочлен p. В общем случае это неверно. Полиномиальная функция одного действительного переменного называется целой рациональной функцией.
полностью определит многочлен p. В общем случае это неверно. Полиномиальная функция одного действительного переменного называется целой рациональной функцией.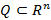 – замкнутый параллелепипед и
– замкнутый параллелепипед и 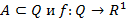 – ограниченная функция. Характеристическая функция или индикатор множества A - функция следующего вида
– ограниченная функция. Характеристическая функция или индикатор множества A - функция следующего вида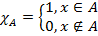
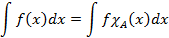
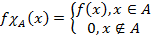
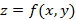 обозначается следующим видом
обозначается следующим видом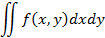
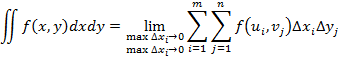
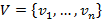 и множества дуг
и множества дуг 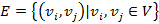 , иными словами
, иными словами 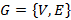 , где
, где 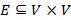 . Граф можно изображать графически, при этом вершины изображают геометрическими фигурами обычно в одной плоскости, при наличии дуги
. Граф можно изображать графически, при этом вершины изображают геометрическими фигурами обычно в одной плоскости, при наличии дуги 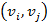 в множестве E, такие вершины соединяет дуга с обозначением стрелкой направления от начальной вершины к конечной. Такой граф называется ориентированным графом.
в множестве E, такие вершины соединяет дуга с обозначением стрелкой направления от начальной вершины к конечной. Такой граф называется ориентированным графом.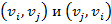 , тогда вместо них изображают одно ребро без указания направления. Дуга вида
, тогда вместо них изображают одно ребро без указания направления. Дуга вида 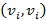 называется петлей, на которой направление выбирается произвольно или не указывается. В общем случае дуги могут быть кратными, иными словами, начальные и конечные вершины соединяют несколько различных дуг. При этом говорят о наличии дуги с некоторой кратностью – числом повторений.
называется петлей, на которой направление выбирается произвольно или не указывается. В общем случае дуги могут быть кратными, иными словами, начальные и конечные вершины соединяют несколько различных дуг. При этом говорят о наличии дуги с некоторой кратностью – числом повторений.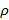 между элементами некоторого множества, которые являются для графа множеством вершин. Если между двумя элементами есть такое отношение, тогда множество дуг графа E имеет такую дугу.
между элементами некоторого множества, которые являются для графа множеством вершин. Если между двумя элементами есть такое отношение, тогда множество дуг графа E имеет такую дугу.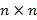 , где n – число вершин графа; в клетке
, где n – число вершин графа; в клетке 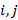 таблица указывается ноль при отсутствии дуги
таблица указывается ноль при отсутствии дуги 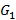 является подграфом для
является подграфом для 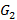 , если его вершины являются подмножеством для множества вершин
, если его вершины являются подмножеством для множества вершин 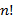 перестановок.
перестановок.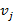 называется достижимой из
называется достижимой из 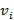 в графе, если в этом графе имеется хотя бы один маршрут из
в графе, если в этом графе имеется хотя бы один маршрут из 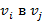 . Граф называют односвязным, если из любой его вершины существует маршрут в любую другую.
. Граф называют односвязным, если из любой его вершины существует маршрут в любую другую.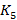 или
или 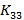 .
.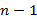 ребер. Дерево может изображаться вертикально с возрастанием или убыванием номера вершин от 1 до n.
ребер. Дерево может изображаться вертикально с возрастанием или убыванием номера вершин от 1 до n. с их совокупностью
с их совокупностью 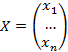 , тогда функция имеет вид
, тогда функция имеет вид 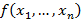 или
или 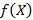 – функция цели или целевая функция.
– функция цели или целевая функция.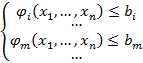
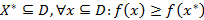 для минимизации целевой функции. В зависимости от характера измерений переменных и вида целевой функции методы оптимизации делятся на непрерывные (с применением производной), дискретные (при не более, чем счетном множестве) и смешанные.
для минимизации целевой функции. В зависимости от характера измерений переменных и вида целевой функции методы оптимизации делятся на непрерывные (с применением производной), дискретные (при не более, чем счетном множестве) и смешанные.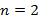 площадью или при
площадью или при  объемом, находятся точки без уловного экстремума в этой области. Исследованием функции на непрерывность и дифференцируемость для каждой перемеренной находятся частные производные. Необходимым условием экстремума дифференцируемой функции является одновременное равенство нулю всех частных производных, что дает координаты предполагаемого экстремума
объемом, находятся точки без уловного экстремума в этой области. Исследованием функции на непрерывность и дифференцируемость для каждой перемеренной находятся частные производные. Необходимым условием экстремума дифференцируемой функции является одновременное равенство нулю всех частных производных, что дает координаты предполагаемого экстремума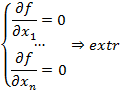
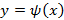 или
или 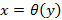 при
при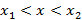 , тогда подстановка этого выражения даст функцию одной переменной, которая исследуется на экстремум на заданном промежутке. Если оптимизируется некоторая функция
, тогда подстановка этого выражения даст функцию одной переменной, которая исследуется на экстремум на заданном промежутке. Если оптимизируется некоторая функция  при ограничении
при ограничении 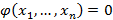 , тогда составляется функция Лагранжа следующего вида
, тогда составляется функция Лагранжа следующего вида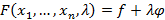
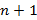 переменной, исследуем на экстремум и решаем следующую систему
переменной, исследуем на экстремум и решаем следующую систему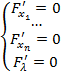
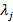 .
.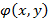 параметр
параметр 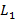 задает плоскую линию. Если наложить на плоскость систему координат, тогда получим функцию
задает плоскую линию. Если наложить на плоскость систему координат, тогда получим функцию 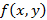 , из которой получим поверхность отклика вида
, из которой получим поверхность отклика вида 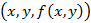 , где система
, где система 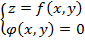 задает пересечение цилиндрической поверхности с поверхностью
задает пересечение цилиндрической поверхности с поверхностью 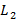 поверхности отклика.
поверхности отклика.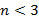 можно допустимую область изобразить на плоскости или пространстве. Такие области являются пересечением полуплоскостей или полупространств, ограниченными функциями соответствующей мерности.
можно допустимую область изобразить на плоскости или пространстве. Такие области являются пересечением полуплоскостей или полупространств, ограниченными функциями соответствующей мерности.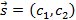 или пропорциональный ему, далее проводится плоскость перпендикулярная вектору. Оптимизация целевой функции состоит в параллельном перемещении до тех пор, пока не исчезнут общие точки с допустимой областью. Последняя из таких линий имеет максимальное значение фикции. Точка
или пропорциональный ему, далее проводится плоскость перпендикулярная вектору. Оптимизация целевой функции состоит в параллельном перемещении до тех пор, пока не исчезнут общие точки с допустимой областью. Последняя из таких линий имеет максимальное значение фикции. Точка 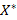 - точка оптимума. При минимизации процесс аналогичен, но линию уровня передвигают в сторону, обратную направлению движения градиента по области допустимых значений.
- точка оптимума. При минимизации процесс аналогичен, но линию уровня передвигают в сторону, обратную направлению движения градиента по области допустимых значений.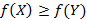 .
.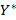 , при этом
, при этом 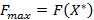 и
и 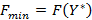 .
.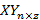 заданы пары значений
заданы пары значений 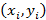 . Каждую такую пару можно считать координатами точки на плоскости. Часть плоскости с этими точками называют полем корреляции. Можно составить функцию, которая задает значения
. Каждую такую пару можно считать координатами точки на плоскости. Часть плоскости с этими точками называют полем корреляции. Можно составить функцию, которая задает значения 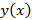 для всех точек, соединяющей их ломаной линией или непрерывной гладкой – интерполяционного многочлена.
для всех точек, соединяющей их ломаной линией или непрерывной гладкой – интерполяционного многочлена. , тогда
, тогда 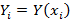 при этих параметрах. Рассмотрим вспомогательную функцию, которая описывает среднее отклонение точек следующего вида
при этих параметрах. Рассмотрим вспомогательную функцию, которая описывает среднее отклонение точек следующего вида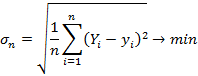
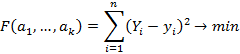
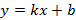 , тогда получим функцию следующего вида
, тогда получим функцию следующего вида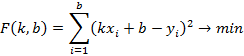
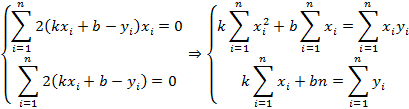
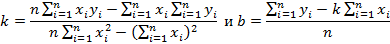
 , которые называют нижней ценой игры. Число
, которые называют нижней ценой игры. Число 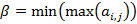 – верхняя цена игры.
– верхняя цена игры.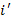 и столбец
и столбец 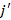 являются оптимальными стратегиями для двух игроков. При условии значительно большей верхней цены игры по отношению к нижней цене игры, у игры нет оптимальной стратегии для обоих игроков.
являются оптимальными стратегиями для двух игроков. При условии значительно большей верхней цены игры по отношению к нижней цене игры, у игры нет оптимальной стратегии для обоих игроков.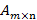 , где игра не имеет седловой точки, следовательно оптимальные стратегии для обоих игроков являются смешанными и имеют следующий вид:
, где игра не имеет седловой точки, следовательно оптимальные стратегии для обоих игроков являются смешанными и имеют следующий вид: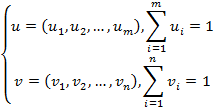
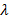 – цене игры.
– цене игры.


