Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции в точке
Функция
Если нарушено требование непрерывности, тогда функция имеет разрыв. Разрывы могут быть двух видов: разрывы с различным левым и правым пределом и разрывы, предел в которых равен бесконечности. Если Пусть
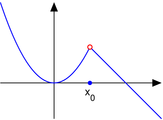
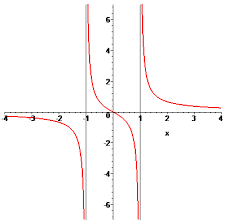
Рисунок 40. Разрыв первого рода. Если не выполняется условие разрыва первого рода, тогда такой разрыв – разрыв второго рода. Пример разрыва второго рода представлен на рисунке 41.
Рисунок 41. Разрыв второго рода. Все элементарные функции непрерывны во всех точках своей области определения. Теорема: Если
Непрерывность функции на отрезке Функция называется непрерывной на интервале Функция называется непрерывной на отрезке Свойства функция непрерывных на отрезке: 1. Если функция 2. Если функция 3. Если
4. Если
Сравнение БМФ и ББФ Пусть
Если
Частный случай при
Теорема: В случае неопределенности
Если числитель и знаменатель представлены произведением функций, тогда множитель также можно заменить на эквивалентный. Нельзя менять на эквивалентные в случае суммы. Пусть
Аналогично анализируются ББФ, для которых также справедливы указанные соотношения.
Производная Пусть задана непрерывная в точке Знаки приращения функции и приращения аргумента будут совпадать для возрастающих функций или будут противоположными при убывающих функций. Предел отношения приращения функции к приращению аргумента при
Производная в некоторой точке Производные некоторых элементарных функций
В физическом смысле производная позволяет найти мгновенную скорость тела в заданный момент времени используя функцию расстояния. Пусть найдена производная некоторой функции и равна
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.21.30 (0.011 с.) |
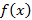 называется непрерывной в точке
называется непрерывной в точке 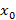 , если существует конечный предел равный значению этой функции в этой точке
, если существует конечный предел равный значению этой функции в этой точке
 непрерывны в точке
непрерывны в точке 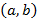 , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.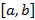 , если она непрерывна в каждой точке этого интервала
, если она непрерывна в каждой точке этого интервала  ; Непрерывность на интервале не гарантирует ни наличие M и m, ни их достижения.
; Непрерывность на интервале не гарантирует ни наличие M и m, ни их достижения. обязательно принимает в некоторой точке
обязательно принимает в некоторой точке  . Если непрерывности на отрезке нет, тогда некоторые промежуточные значения могут не приниматься такой функцией;
. Если непрерывности на отрезке нет, тогда некоторые промежуточные значения могут не приниматься такой функцией; и
и 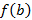 имеют разные знаки, тогда существует точка
имеют разные знаки, тогда существует точка 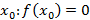 .
.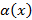 и
и 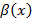 – БМФ при
– БМФ при 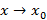 или
или  , тогда при
, тогда при 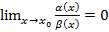 функция
функция 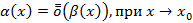
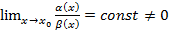 , тогда
, тогда 
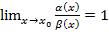 , тогда
, тогда 
 весь числитель и весь знаменатель можно заменить на эквивалентные функции
весь числитель и весь знаменатель можно заменить на эквивалентные функции
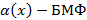 при
при 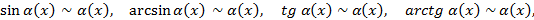

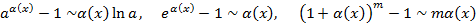
 , тогда получим приращение функции в точке
, тогда получим приращение функции в точке 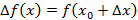 . Приращение аргумента может быть как больше нуля, так и меньше, что задает правое и левое движение по указанной функции. В связи с этим приращение функции также может быть больше или меньше нуля.
. Приращение аргумента может быть как больше нуля, так и меньше, что задает правое и левое движение по указанной функции. В связи с этим приращение функции также может быть больше или меньше нуля.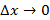 называется производной функции
называется производной функции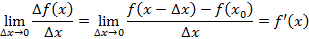
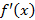 – функция.
– функция. ,
, 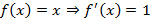 ,
, 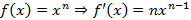
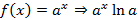 ,
, 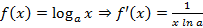
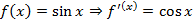 ,
, 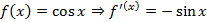 ,
, 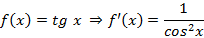
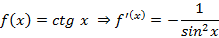
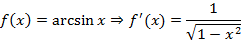
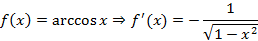
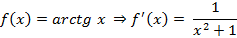
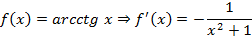
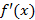 , поскольку это также функция, тогда для нее тоже можно искать производную. Производная любого порядка примет вид
, поскольку это также функция, тогда для нее тоже можно искать производную. Производная любого порядка примет вид