
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательная к графику функции
Пусть дана некоторая кривая и фиксированная точка
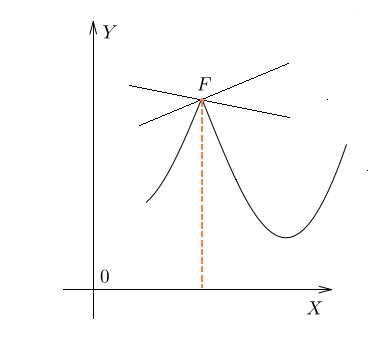
Рисунок 42. Построение касательной к графику функции. Касательная существует не всегда. Например, на рисунке 43 показано, что у некоторого графика функции при выборе точки, предельное положение секущей различны.
Рисунок 43. Пример функции, когда касательная не существует в точке F. Рассмотрим график функции
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функций в этой точке – геометрический смысл производной. Уравнение касательной примет вид
Нормалью к графику функции в точке
Рисунок 44. Нормаль относительно касательной к графику функции. Уравнение нормали, учитывая ее расположение относительно касательной, примет вид
Дифференциал Пусть функция
Приращение дифференцируемой функции состоит из двух частей: Главная линейная часть приращения называется дифференциалом
Геометрический смысл дифференциала – приращение касательной к функции. Обозначение производной функции – отношение дифференциалов функции и переменной
При фиксированной точке
Правила дифференцирования
Теорема Лопиталя: Пусть
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.77.195 (0.005 с.) |
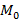 на ней. Выберем произвольную точку
на ней. Выберем произвольную точку 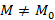 на этой же кривой и проведем секущую. Пусть
на этой же кривой и проведем секущую. Пусть 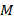 движется по кривой к
движется по кривой к 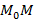 меняет свое положение. Если в момент слияния
меняет свое положение. Если в момент слияния  секущая занимает однозначное положение, тогда это предельное положение секущей, которая называется касательной. Все вышеуказанные построения представлены на рисунке 42.
секущая занимает однозначное положение, тогда это предельное положение секущей, которая называется касательной. Все вышеуказанные построения представлены на рисунке 42.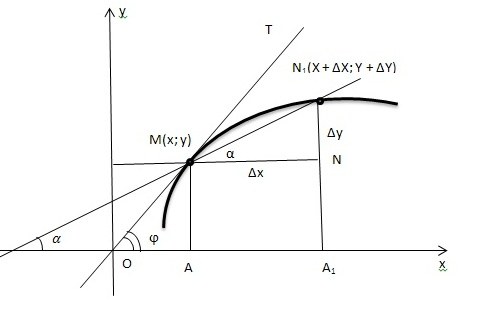
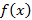 , на котором зафиксирована точка
, на котором зафиксирована точка 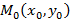 на графике и выбрана произвольная
на графике и выбрана произвольная 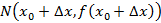 , как указано на рисунке 42. Обозначим
, как указано на рисунке 42. Обозначим 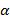 – угол наклона секущей;
– угол наклона секущей; 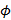 – угол наклона касательной
– угол наклона касательной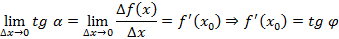
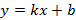 , поскольку касательная проходит через точку
, поскольку касательная проходит через точку 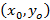 , где
, где 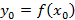 , тогда уравнение касательной примет вид
, тогда уравнение касательной примет вид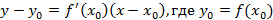
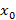 называется прямая перпендикулярная касательной, построенной в этой же точке. Пример нормали к графику функции представлен на рисунке 44.
называется прямая перпендикулярная касательной, построенной в этой же точке. Пример нормали к графику функции представлен на рисунке 44.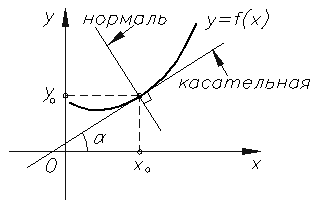
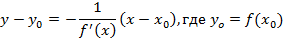
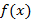 имеет в точке
имеет в точке 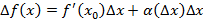
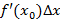 – пропорциональна приращению аргумента и
– пропорциональна приращению аргумента и 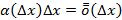 – малая по сравнению с приращением аргумента – первая главная линейная часть приращения.
– малая по сравнению с приращением аргумента – первая главная линейная часть приращения.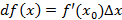
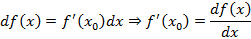
 , изменение которого меняет дифференциал.
, изменение которого меняет дифференциал.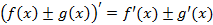
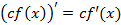
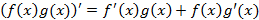
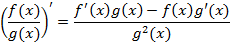
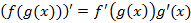
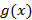 непрерывные и дифференцируемые функции в окрестности точки
непрерывные и дифференцируемые функции в окрестности точки 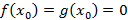 , тогда
, тогда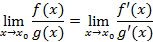
 и
и  .
.


