Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменной в определенном интегралеСодержание книги
Поиск на нашем сайте
Пусть
Замена переменной чаще производится справа на лево следующим образом
Интегралы вида
В данном случае происходят следующие замены: Второй способ подразумевает использование соотношения Интегрирование по частям Пусть
Данное соотношение можно упростить, если произвести две замены следующего вида
Основные виды интегралов, берущихся по частям имеют вид
В данных соотношениях P(x) и Q(x) - некоторые многочлены.
Рациональные функции Функция, представленная как отношение двух многочленов называется рациональной функцией R(x)
Рациональная функция называется правильной, если Любую неправильную рациональную дробь можно разложить в сумму многочлена и правильной рациональной дроби. Такой прием можно использовать при интегрировании рациональных функций. Элементарные рациональные дроби – правильные рациональные функции следующих четырех типов
Интегрирование элементарных дробей первых трех типов соответственно имеет вид
Теорема: Любой многочлен можно представить как произведение скобок вида Любую правильную рациональную дробь можно разложить в в сумму элементарных дробей по следующему алгоритму 1. Готовим знаменатель по указанной выше теореме; 2. Каждой скобке знаменатель ставим в соответствие в группу элементарных по следующим правилам
Коэффициенты A и B находятся методом неопределенных значений или методом произвольных значений. Метод неопределенных значений подразумевает приравнивание числительных при одинаковых знаменателях, после чего производится подбор коэффициентов. Метод произвольных значений подразумевает подстановку x в обе части получаемого уравнения и подбор коэффициентов.
Определенный интеграл
Назовем определенным интегралом на отрезке
Данное соотношение – формула Ньютона-Лейбница. Функция должна быть непрерывна. Если
Рисунок 49. Геометрический смысл определенного интеграла. Свойства определенного интеграла: 1. 2. 3. 4. 5. Пусть
Данное соотношение определяет способ замены переменной в определенном интеграле. Пусть
Данное соотношение определяет интегрирование по частям для определенного интеграла. Определенный интеграл имеет следующие приложения 1. Определение площади криволинейной трапеции Если
Рисунок 50. Знакопеременная функция сигнала. 2. Вычисление длины кривой Пусть
3. Вычисление объемов тел вращения Пусть
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.150.38 (0.01 с.) |

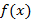 непрерывная функция,
непрерывная функция, 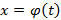 – непрерывно-дифференцируемая функция, тогда справедливо соотношение, которое можно получить формальной заменой
– непрерывно-дифференцируемая функция, тогда справедливо соотношение, которое можно получить формальной заменой 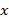 на
на 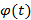
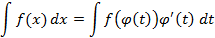
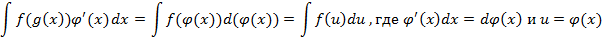
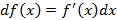 – вынесение из дифференциала;
– вынесение из дифференциала;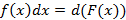 – поднесение под дифференциал;
– поднесение под дифференциал;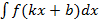 можно вычислять двумя способами
можно вычислять двумя способами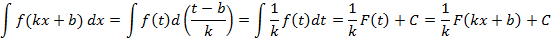
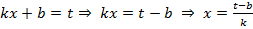 , из которых вытекает соотношение:
, из которых вытекает соотношение: 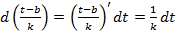 .
. .
.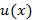 и
и 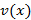 – непрерывно-дифференцируемые функции, тогда справедливо следующие соотношение
– непрерывно-дифференцируемые функции, тогда справедливо следующие соотношение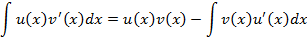
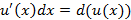 и
и 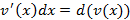 , тогда получим
, тогда получим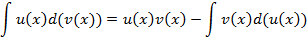
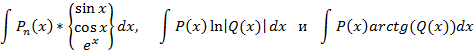
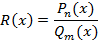
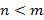 или неправильной, если
или неправильной, если 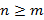 .
.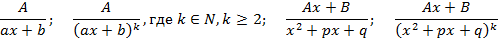
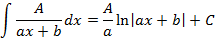
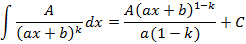
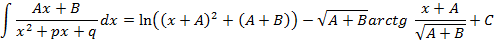
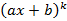 и
и 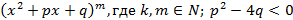 .
.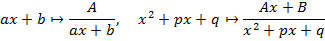
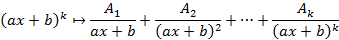
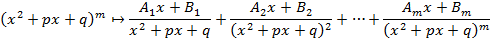
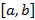 от функции
от функции 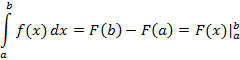
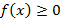 на отрезке
на отрезке 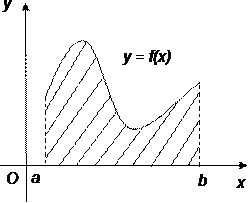
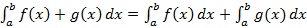 ;
;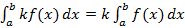 ;
;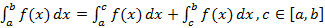 ;
;
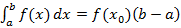 .
.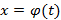 непрерывно-дифференцируемая на
непрерывно-дифференцируемая на 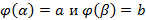 , тогда
, тогда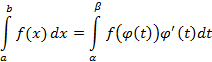
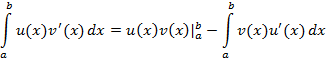
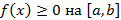 , тогда
, тогда 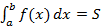 . В случае знакопременности функции
. В случае знакопременности функции 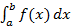 – алгебраическая сумма площадей криволинейных трапеций, разделенных нулями, заданными функции (пример указан на рисунке 50).
– алгебраическая сумма площадей криволинейных трапеций, разделенных нулями, заданными функции (пример указан на рисунке 50).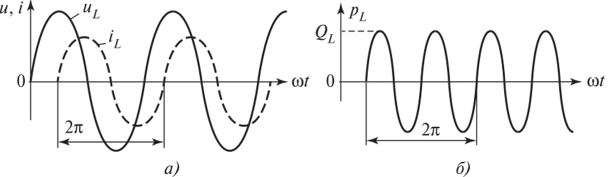
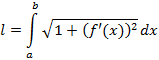
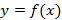 непрерывна на отрезке
непрерывна на отрезке