
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двоичный сумматор последовательного действия и сравнение на равенствоСодержание книги
Поиск на нашем сайте
Двоичный сумматор последовательного действия (ДСПД) – устройство, имеющие два входа на которые поступают Входным алфавитом является набор бинарных пар вида
Устройство, в котором на входе находятся два числа Одну и ту же цепочку можно получить, применяя правила в различных последовательностях, когда деревья выводов различны. Если на каждом шаге для однозначности в процессе вывода применять правило к самому левому или правому петерминалу в сентенциальной форме, тогда получим левосторонний и правосторонний вывод. Исходя из этого: 1. Каждому дереву соответствует один или множество выводов; 2. Каждому дереву соответствует единственный правый или единственный левый выводы; 3. Если в каждый цепочке, выводимой в данный грамматике, соответствует единственное дерево вывода, тогда такая грамматика является однозначной, следовательно в каждом правиле грамматики не более одного петерминала. Языком Для классификации грамматик применяют иерархию Хомского, содержащую четыре типа грамматик: 1. Правила вида 2. Правила вида 3. Правила вида 4. Автоматные грамматики вида Каждый тип включает грамматики более высоких уровней как частные случаи.
Для построения распознавателей грамматик часто необходимо преобразовывать правила исходной грамматики к новому виду. При этом язык, порождающий исходной и полученной грамматик, меняться не должен. Две грамматики эквивалентны, если они порождают один и тот же язык или одни и те же цепочки терминальных символов. Для получения эквивалентной грамматики допустимы следующие операции: удаление или добавление бесполезных нетерминалов – непродуктивных или недостижимых. Непродуктивный нетерминал – нетерминал, из которого нельзя получить цепочку терминалов единичной или более длиной. Для их поиска необходимо: если все правила правой части продуктивны, тогда продуктивны и все правила в левой части, тогда для поиска непродуктивных нетерминалов нужно составить список всех правил из левой части. Если найдется правило такое, что все нетерминалы в правой части уже занесены в список, тогда из левой части нетерминалы добавляются в этот список. Продолжая процесс многократно, при отсутствии добавлений списка процесс завершается. Нетерминалы, не попавшие в список, являются непродуктивными и содержащие их правила можно удалить. Недостижимый терминал – нетерминал, который не участвует в процессе. Для поиска недостижимых нетерминалов используют свойство: если нетерминал левой части правила достижимы, тогда правило в правой части так же достижимо. Алгоритм поиска недостижимых нетерминалов: 1. Образовать одноэлементный список начального нетерминала; 2. Если во множестве P найдено правило, которое есть в списке, тогда в список добавляют все нетерминалы в его правой части. При неизменности списка получены все достижимые нетерминалы. Не попавшие в этот список являются недостижимыми, тогда их можно исключить. После удаления всех непродуктивных и недостижимых нетерминалов и содержащих их правил из P получим эквивалентную грамматику, реализующую тот же язык. Любое регулярное множество, которое распознает конечный автомат, можно описать с помощью автоматной грамматики. Алгоритм получения грамматики конечного автомата: 1. Начальное состояние конечного автомата – начальный символ грамматики – первый нетерминал;
2. Все символы без конца цепочки – все терминальные символы грамматики; 3. Конец строки – второй нетерминальный символ; 4. Множество состояний автомата – нетерминальные символы грамматики; 5. Если в таблице переходов есть переход из A и B при входном x, тогда получаем правило 6. Если D – допустимое состояние автомата, тогда вводится правило Если обработаны все непустые клетки таблицы переходов, тогда составление правил завершено.
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.183.122 (0.007 с.) |

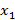 и
и 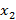 начиная с младших разрядов, а на выходе имеется двоичная запись числа
начиная с младших разрядов, а на выходе имеется двоичная запись числа 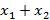 .
.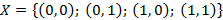 и выходным алфавитом вида
и выходным алфавитом вида 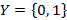 . Состояние автомата определяется значением переноса при сложении двоичных разрядов
. Состояние автомата определяется значением переноса при сложении двоичных разрядов 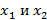 , если при таком сложении образовывается перенос, тогда сумматор переходит в состояние
, если при таком сложении образовывается перенос, тогда сумматор переходит в состояние 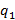 и при отсутствии переноса
и при отсутствии переноса 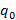 .
.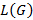 порождаемым грамматикой G является множество всех цепочек
порождаемым грамматикой G является множество всех цепочек 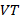 , выводимых из начальной грамматики.
, выводимых из начальной грамматики.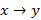 , где x, y – любые цепочки терминалов и нетерминалов – 0-ой тип;
, где x, y – любые цепочки терминалов и нетерминалов – 0-ой тип;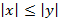 – 1-ый тип с фразовой структурой;
– 1-ый тип с фразовой структурой;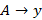 , где A – нетерминал, y – любая цепочка – 2-ой тип с контекстно-зависимой фразовой структурой;
, где A – нетерминал, y – любая цепочка – 2-ой тип с контекстно-зависимой фразовой структурой;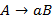 ,
, 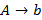 или
или 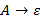 , где A, B – нетерминалы; a, b – терминалы,
, где A, B – нетерминалы; a, b – терминалы, 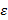 – пустая цепочка – 3-ий тип с контекстно-независимой фразовой структурой.
– пустая цепочка – 3-ий тип с контекстно-независимой фразовой структурой.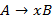 ;
;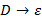 , где
, где 


