
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Машина Поста и машина Тьюринга
Автоматы с магазинной памятью или магазинные автоматы (МП-автоматы) образуют класс распознающих моделей для контекстно-свободных языков аналогично тому, как конечные автоматы являются распознающими моделями в классе регулярных языков. МП-автомат – устройство, имеющие блок управления, входную ленту, считывающую головку и блок внутренней памяти в виде очереди или стека. Схематическое изображение магазинного автомата представлено на рисунке 69.
Рисунок 69. Автомат с магазинной памятью. Финитные комбинаторные процессы основаны на формальном описании алгоритмов, как общей проблемы, которые должны при решении частной проблемы должны относиться к общей проблеме. Пространство символов (язык), в котором задается конкретная проблема и получается ответ с набором инструкций, иными словами, операции в пространстве символов, задающих как сами операции, так и порядок выполнения инструкций. Пространство символов Поста – бесконечная лента ячеек, в которой каждая ячейка может быть помечена или не помечена. Конкретная проблема задается «внешней силой» (термин Поста) в виде пометки конечного количества ячеек. Любая конфигурация начинается и заканчивается помеченной ячейкой, между которыми может быть несколько помеченных цепочек, разделенных некоторым количеством непомеченных ячеек. После применения к конкретной проблеме некоторого набора инструкций ее решение представляется также в виде набора помеченных или непомеченных ячеек, который распознается той же «внешней силой». Машина Поста обладает следующим набором инструкций: 1. Пометить ячейку, если она пуста; 2. Стереть метку, если она есть; 3. Переместиться влево на одну ячейку; 4. Переместиться вправо на одну ячейку; 5. Определить наличие метки ячейки; 6. Остановиться; Набор перечисленных инструкций – минимальный набор бытовых операций. Программа для такой машины Поста представляет собой нумерованную последовательность инструкций, причем для пятой инструкции указывается два дополнительных набора инструкций: исходя из результата инструкции, перейти на первую или вторую инструкцию. Основные требования к машине Поста: 1. Не возникает коллизий в первой и второй инструкциях;
2. Набор инструкций заканчивается за конечное количество шагов; 3. Набор инструкций задает финитный первый процесс, если набор инструкций заканчивается; Финитный первый процесс – первое решение общей проблемы, если ответ для каждой конкретной проблемы правильный, что определяется «внешней силой». Поскольку множество проблем, образующих общую проблему, счетное, тогда можно образовать биекцию между множествами проблем и натуральных чисел. Общая проблема – первая заданная проблема, если существует такой финитный первый процесс, что применимый к Машина Тьюринга состоит из двух основных частей: бесконечная лента и автомат. Лента используется для хранения информации, она бесконечна в обе стороны и разбита на ячейки, которые не нумеруются. В каждой клетке может быть записан один из символов входного алфавита или ничего не записано (пустое обозначение - Автомат в каждый момент времени считывает ровно одну ячейку ленты – видимую клетку, где записан видимый символ. Автомат может находится в одном из конечного числа состояний, одно из которых – начальное для машины Тьюринга. Пара Автомат может выполнить три элементарных действия: 1. Записать в видимую клетку новый символ; 2. Сдвинуться на одну клетку влево или вправо; 3. Перейти в другое состояние или остаться в прежнем. Машина Тьюринга работает тактами, которые выполняются один за другим. На каждом такте выполняются три действия в произвольном порядке. Если на очередном такте какое-либо из трех составляющих остается неизменным, тогда в тройке эту составляющую пропускают, ее наличие показывает запятая.
Универсальная машина Тьюринга – машина Тьюринга, которая на вход сообщения любой другой машины Тьюринга вместе с закодированным кодом для нее. Возможна модуляция другой машины Тьюринга с ростом количества шагов. На выходе получаем выход другой машины Тьюринга. Кодирование и декодирование необходимы, поскольку входной алфавит универсальной машины Тьюринга фиксированный и моделируемая машина Тьюринга может пользоваться другим алфавитом. Полный по Тьюрингу автомат – автомат, способный эмулировать работу другого автомата. Многоленточная машина Тьюринга – расширение машины Тьюринга, полученное за счет механического дублирования памяти. При этом потенциально бесконечных лент и считывателей несколько, но конечное число. Исходя из этого, входной сигнал – множество символов, считаных со всех лент и выходной сигнал – множество символов, записанных на все ленты и векторов действий для всех считывателей. Многоленточную машину Тьюринга можно смоделировать одноленточной машиной Тьюринга. Двумерная машина Тьюринга – принимает на вход матрицу входных данных, где матрица – неограниченное поле ячеек. Двумерную машину Тьюринга можно смоделировать двуленточной машиной Тьюринга, в которой одна лента – взаимодействия по горизонтали, а вторая лента – по вертикали или положение считывается по матрице.
Математические Функции Вычислительной функцией является такая, для которой может быть сконструирован конечный автомат такой, что для любого аргумента вычисляется значение функции, после чего останавливается. Аргумент и результат функции должны быть конечны, следовательно множество всех вычислительных функций можно считать подмножеством функций следующего вида
Теорема о существовании невычислимых функций: Множество вычислимых функций является строгим подмножеством для множества функций. Иными словами, среди функций существуют невычислимые. Рассмотрим более простые функции Теорема: Любую вычислительную функцию можно реализовать машиной Тьюринга. Для машины Тьюринга входной алфавит и множество состояний являются конечными, следовательно такая машина описывается набором команд. Если записать их подряд с разделителем, тогда каждая машина Тьюринга однозначно задается одним длинным словом. При этом любую машину Тьюринга описываемым конечным словом, множество всех машин Тьюринга – множество таких слов, которые являются счетными. Множество вычислимых функций, описываемых некоторой машиной Тьюринга, является счетным. Множество всех алгоритмов как множество всех функций – несчетно. Исходя из этого, имеются невычислимые функции, иными словами множество вычислимых функций является подмножеством для множества функций. Счетное множество называют вычислимым, если его индикатором является вычислимая функция. Дополнение вычислимого множества также вычислимо. Счетное множество является полу разрешимым, если существует автомат, который для каждого элемента множества корректно вычисляет индикатор: для принадлежащих множеству дает значение единица, для не принадлежащих – ноль или зависает.
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.88.249 (0.007 с.) |
 числу ячеек, в качестве исходной конфигурации, он задает n-проблему в виде набора помеченных ячеек.
числу ячеек, в качестве исходной конфигурации, он задает n-проблему в виде набора помеченных ячеек.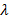 ). Действие записи в ячейку
). Действие записи в ячейку 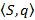 видимого символа S и текущего состояния q образует конфигурацию.
видимого символа S и текущего состояния q образует конфигурацию.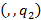 – считываемый символ на ленте остается неизменным (первая позиция), сдвига считывающей головки нет (вторая позиция), состояние автомата меняется на
– считываемый символ на ленте остается неизменным (первая позиция), сдвига считывающей головки нет (вторая позиция), состояние автомата меняется на 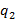 . Формально можно считать, что в программе машины Тьюринга имеется дополнительное состояние – завершающее состояние.
. Формально можно считать, что в программе машины Тьюринга имеется дополнительное состояние – завершающее состояние.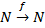
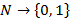 – предикаты с логическим значением, определенные на любом натуральном числе. Такие предикаты являются несчетными, поскольку они являются подмножеством для множества функций, которое может быть только несчетным.
– предикаты с логическим значением, определенные на любом натуральном числе. Такие предикаты являются несчетными, поскольку они являются подмножеством для множества функций, которое может быть только несчетным.


