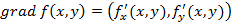Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные функции двух переменныхСодержание книги
Поиск на нашем сайте
Для функций двух переменных можно внести понятия предела и непрерывности. Пусть Рассмотрим пределы отношения частного приращения функции по x и y к соответствующим аргументам, тогда получим частные производные функции по x и y соответственно
Обе частные производные являются по сути обычной производной функции одной переменной, которая появляется при фиксации второй переменной. Исходя из этого все правила и свойства сохраняются. Геометрически частная производная
Рисунок 56. Касательные, проведенные к графику функции двух переменных.
Дифференцируемость и дифференциал функции двух переменных Для функции двух переменных существование конечных частных производных не гарантирует не только гладкость, но и непрерывность. Если непрерывная функция
Дифференцируемость геометрически означает гладкость графика функции двух переменных, из чего следует, что к данному графику можно провести касательную плоскость. У дифференцируемой функции двух переменных в точке
Пример касательной плоскости к функции двух переменных представлен на рисунке 57.
Рисунок 57. Касательная плоскость.
Производная по направлению Пусть
Геометрически производная по направлению характеризует скорость изменения функции Для дифференцируемой функции
В данном соотношении
Градиент Градиентом функции двух переменных называется вектор, координаты которого составлены из частных производных рассматриваемой функции
Если в каждой точке области определения функции построить вектор градиента, тогда получим векторное поле градиентов. Свойства градиента: 1. В каждой точке вектор градиента задает направление, в котором функция растет быстрее всего; 2. Вектор, противоположный градиенту, указывает направление, в котором функция убывает быстрее всего; 3. Если взять в точке прямую, перпендикулярную градиенту, тогда она будет касательной к линии уровня, проходящей через точку.
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.94 (0.007 с.) |

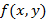 – непрерывная функция, тогда
– непрерывная функция, тогда 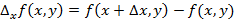 – частное приращение функции по x. Аналогично число
– частное приращение функции по x. Аналогично число 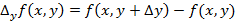 – частное приращение по y. Число
– частное приращение по y. Число 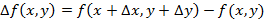 – полное приращение функции.
– полное приращение функции.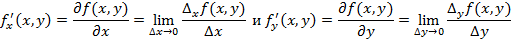
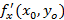 равна тангенсу угла наклона касательной, проведенной к кривой, получающейся при сечении поверхности графика вертикальной плоскостью
равна тангенсу угла наклона касательной, проведенной к кривой, получающейся при сечении поверхности графика вертикальной плоскостью 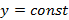 . Аналогично для частной производной
. Аналогично для частной производной 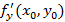 , в данном случае сечение поверхности графика – вертикальная плоскость
, в данном случае сечение поверхности графика – вертикальная плоскость 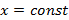 . Пример проведения касательных
. Пример проведения касательных  к графику функции двух переменных приведен на рисунке 56.
к графику функции двух переменных приведен на рисунке 56.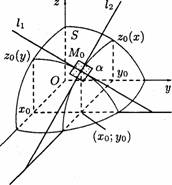
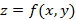 в точке
в точке 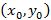 имеет полное приращение
имеет полное приращение 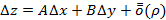 , где
, где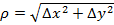 , тогда функцию называют дифференцируемой в точке
, тогда функцию называют дифференцируемой в точке 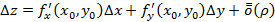
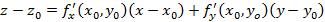
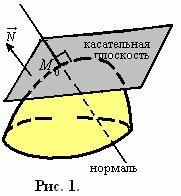
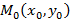 – некоторая точка в области определения данной функции,
– некоторая точка в области определения данной функции, 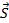 – вектор в плоскости xOy. Рассмотрим приращение
– вектор в плоскости xOy. Рассмотрим приращение 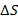 в точке
в точке 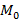 в направлении вектора
в направлении вектора 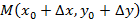 . Возьмем полное приращение
. Возьмем полное приращение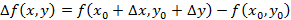 и рассмотрим
и рассмотрим 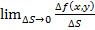 , если этот предел существует и конечен, тогда он называется производной по направлению S функции
, если этот предел существует и конечен, тогда он называется производной по направлению S функции 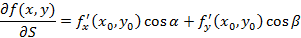
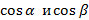 – направляющие косинусы для вектора
– направляющие косинусы для вектора