
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическая и алгебраическая теории чиселСодержание книги
Поиск на нашем сайте
В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа (как вещественного, так и комплексного), иногда также теория дифференциальных уравнений. Это позволило значительно расширить тематику исследований теории чисел. В частности, в неё вошли следующие новые разделы: 1. Распределение простых чисел в натуральном ряду и в других последовательностях (например, среди значений заданного многочлена). 2. Представление натуральных чисел в виде сумм слагаемых определённого вида (простых чисел, квадратов и т. д.). 3. Диофантовы приближения. Первым шагом в применении аналитических методов в теории чисел стал метод производящих функций, сформулированный Эйлером. Для определения количества целочисленных неотрицательных решений линейного уравнения вида
В алгебраической теории чисел понятие целого числа расширяется, в качестве алгебраических чисел рассматривают корни многочленов с рациональными коэффициентами. Была разработана общая теория алгебраических и трансцендентных чисел. При этом аналогом целых чисел выступают целые алгебраические числа, то есть корни унитарных многочленов с целыми коэффициентами. В отличие от целых чисел, в кольце целых алгебраических чисел не обязательно выполняется свойство факториальности, то есть единственности разложения на простые множители. Теория алгебраических чисел обязана своим появлением изучению диофантовых уравнений, и в том числе попыткам доказать великую теорему Ферма. Куммеру принадлежит равенство
После определения алгебраических и трансцендентных чисел в алгебраической теории чисел выделилось направление, которое занимается доказательством трансцендентности конкретных чисел, и направление, которое занимается алгебраическими числами и изучает степень их приближения рациональными и алгебраическими. Одним из основных приёмов является вложение поля алгебраических чисел в своё пополнение по какой-то из метрик — архимедовой (например, в поле вещественных или комплексных чисел) или не архимедовой (например, в поле p-адических чисел).
Математический анализ Числовые последовательности Числовой последовательностью называется бесконечное число занумерованных чисел
Рисунок 30. Отображение чисел на числовой прямой. Помимо вышеуказанных способов, числа можно задать на координатной плоскости, рассмотрев график функции натуральной переменой Последовательность
Геометрически ограниченность последовательности означает, что все элементы находятся на отрезке Последовательность 1. 2. 3. 4. Число A называется пределом последовательности
У последовательности не может быть более одного предела. Свойства конечных пределов: 1. 2. 3. 4. 5. Если
|
||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

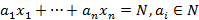
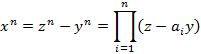
 или
или 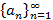 . Задать последовательность можно формулой для
. Задать последовательность можно формулой для 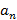 , например,
, например, 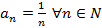 и на числовой оси (рисунок 30).
и на числовой оси (рисунок 30).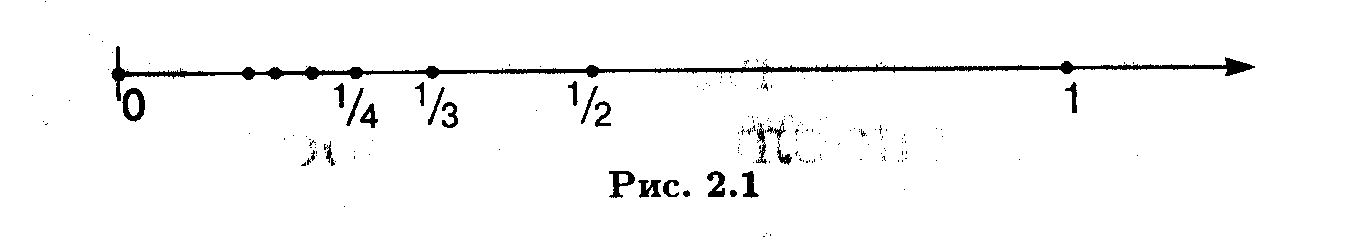
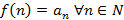 .
.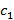 и
и 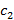 , такие что
, такие что 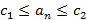 для всех элементов последовательности
для всех элементов последовательности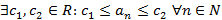
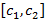 (на рисунке 30 последовательность ограничена отрезком
(на рисунке 30 последовательность ограничена отрезком 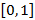 ). В случае рассмотрения последовательности на координатной плоскости, тогда все точки графика находятся внутри полосы, ограниченной
). В случае рассмотрения последовательности на координатной плоскости, тогда все точки графика находятся внутри полосы, ограниченной 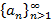 называется монотонной, если выполняется одно из условий:
называется монотонной, если выполняется одно из условий: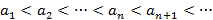 (строго возрастает);
(строго возрастает);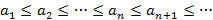 (не убывает);
(не убывает);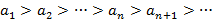 (строго убывает);
(строго убывает);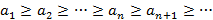 (не возрастает).
(не возрастает).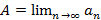 , если для любой
, если для любой 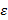 – окрестности точки A (даже для сколь угодно малой) можно указать номер N, который зависит от
– окрестности точки A (даже для сколь угодно малой) можно указать номер N, который зависит от 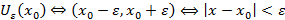

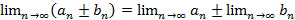 ;
;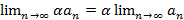 ;
;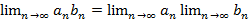 ;
;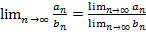 ;
;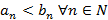 , тогда
, тогда  .
.


