
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое условие сходимости рядаСодержание книги
Поиск на нашем сайте Если ряд Следствие. Если Пример 1. Исследовать сходимость ряда Решение. Найдем
Признак сравнения рядов с неотрицательными членами Пусть даны два ряда с неотрицательными членами
Если Пример 2. Исследовать на сходимость ряд Решение. Т.к. Пример 3. Исследовать на сходимость ряд Решение. Т.к.
Также используется следующий признак сходимости: Теорема. Если
Признак Даламбера Пусть дан ряд Пример 4. Исследовать на сходимость ряд Решение. Пример 5. Исследовать на сходимость ряд Решение.
Признак Коши (радикальный признак)
Пусть дан ряд Пример 6. Определить сходимость ряда Решение. Пример 7. Определить сходимость ряда Решение. Таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Интегральный признак Коши Пусть дан ряд Пример 8. Исследовать на сходимость ряд Решение. Ряд
Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными. Знакочередующиеся ряды Ряд называется знакочередующимся, если положительные и отрицательные члены следуют друг за другом поочередно.
Знакочередующийся ряд можно записать в виде:
Признак Лейбница Если для знакочередующегося ряда Теорема. Пусть дан знакопеременный ряд
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

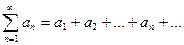 сходится, то общий член ряда а n стремится к нулю (т.е.
сходится, то общий член ряда а n стремится к нулю (т.е. 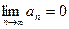 ). Однако это условие не является достаточным. Например, гармонический ряд
). Однако это условие не является достаточным. Например, гармонический ряд 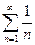 является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.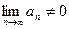 , то ряд расходится.
, то ряд расходится.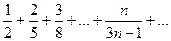
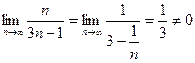 - необходимый признак сходимости не выполняется, значит, ряд расходится.
- необходимый признак сходимости не выполняется, значит, ряд расходится.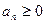 (1)
(1)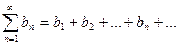 ,
, 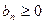 (2)
(2)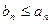 для любого п, то из сходимости ряда (1) следует сходимость ряда (2) и сумма ряда (2) не превосходит суммы ряда (1); из расходимости ряда (2) следует расходимость ряда (1).
для любого п, то из сходимости ряда (1) следует сходимость ряда (2) и сумма ряда (2) не превосходит суммы ряда (1); из расходимости ряда (2) следует расходимость ряда (1).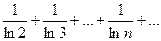
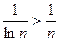 , а гармонический ряд
, а гармонический ряд 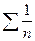 расходится, то расходится и ряд
расходится, то расходится и ряд 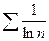 .
.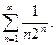
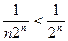 , а ряд
, а ряд 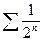 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 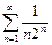 тоже сходится.
тоже сходится.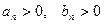 и существует предел
и существует предел 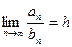 , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды 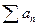 и
и 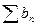 ведут одинаково в смысле сходимости.
ведут одинаково в смысле сходимости.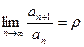 , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то ряд может быть как сходящимся, так и расходящимся.
, то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то ряд может быть как сходящимся, так и расходящимся.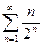 .
.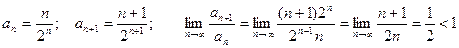 . Следовательно, по признаку Даламбера ряд сходится.
. Следовательно, по признаку Даламбера ряд сходится.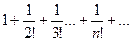
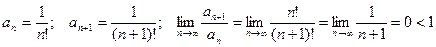 . Следовательно, по признаку Даламбера ряд сходится.
. Следовательно, по признаку Даламбера ряд сходится. , то при q<1 ряд сходится, при q>1 ряд расходится, при q=1 ряд может быть как сходящимся, так и расходящимся.
, то при q<1 ряд сходится, при q>1 ряд расходится, при q=1 ряд может быть как сходящимся, так и расходящимся.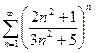 .
.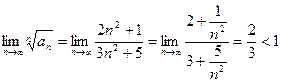 , следовательно, ряд сходится.
, следовательно, ряд сходится.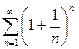 .
.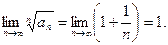 Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю. Найдем
Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю. Найдем 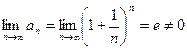 .
.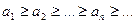 и f(x) – такая непрерывная монотонно убывающая функция, что f(п)=ап. тогда данный ряд и несобственный интеграл
и f(x) – такая непрерывная монотонно убывающая функция, что f(п)=ап. тогда данный ряд и несобственный интеграл 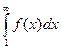 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.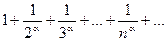
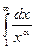 сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд 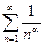 называется обобщенным гармоническим рядом.
называется обобщенным гармоническим рядом.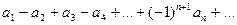 , где
, где 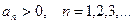
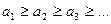 и
и 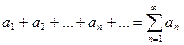 (1) и ряд, составленный из абсолютных величин членов ряда (1):
(1) и ряд, составленный из абсолютных величин членов ряда (1): 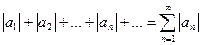 (2). Тогда из сходимости ряда (2) следует сходимость ряда (1).
(2). Тогда из сходимости ряда (2) следует сходимость ряда (1).


