Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С разделяющимися переменнымиСодержание книги
Поиск на нашем сайте
Цель занятия: Научиться решать дифференциальные уравнения первого порядка. Формировать ОК-2, ОК-6, ОК-8. Подготовка к занятию: Повторить теоретический материал по теме «Обыкновенные дифференциальные уравнения». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Дифференциальным уравнением называется уравнение, содержащее независимую переменную х, искомую функцию у и ее производные у ′, у ′′,… Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Символически дифференциальное уравнение первого порядка записывается следующим образом: F (x, y, y ′) = 0 или у ′ = f (x, y) Решением дифференциального уравнения называется всякая функция у = φ (х), которая обращает данное уравнение в тождество. Общим решением дифференциального уравнения называется функция у = φ (х,С), зависящая от постоянной С и удовлетворяющая данному уравнению при любом фиксированном значении этой постоянной.
Частным решением дифференциального уравнения называется решение, полученное из общего решения при фиксированных значениях постоянной. Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = j (х, С 0), удовлетворяющего начальным условиям у (х 0) = у 0. Теорема Коши(теорема о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную Пример 1. Найти общее решение дифференциального уравнения Решение. Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
Теперь интегрируем:
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.125 (0.008 с.) |

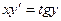
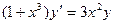
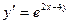

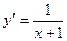
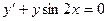
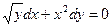

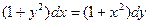

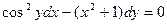
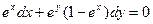



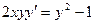
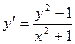
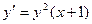
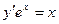
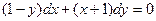

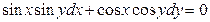
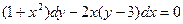

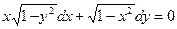
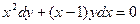 ,
если х = 1, у = 1
,
если х = 1, у = 1
 ,
если х = 0, у = 2
,
если х = 0, у = 2
 ,
если х = 0, у = 4
,
если х = 0, у = 4
 если
если 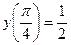
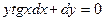 ,
если у = 4,
,
если у = 4, 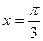
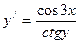 ,
если х = 0, у=
,
если х = 0, у= 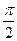
 ,
если у (1) = 3
,
если у (1) = 3
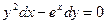 ,
если х = 0, у = 1
,
если х = 0, у = 1

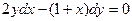 ,
если у (1) = 4
,
если у (1) = 4
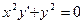 ,
если
,
если 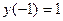
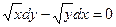 ,
если у = 0, х = 0
,
если у = 0, х = 0
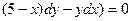 ,
если х = 4, у = 7
,
если х = 4, у = 7
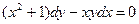 ,
если
,
если 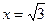 , у = 2
, у = 2
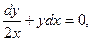 если х = 0, у = 5
если х = 0, у = 5
 ,
если
,
если 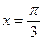 ,
, 
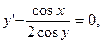 если
если 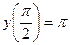
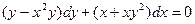 ,
если у (2) = 0
,
если у (2) = 0
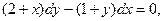 если у (0) = 5
если у (0) = 5
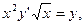 если
если 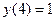
 , если у (3) = 0
, если у (3) = 0
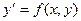 , то какова бы не была точка (х0, у0) в области D, существует единственное решение
, то какова бы не была точка (х0, у0) в области D, существует единственное решение 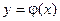 уравнения
уравнения 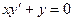 .
.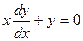
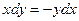
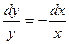
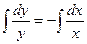
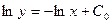
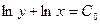
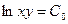
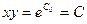
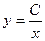 - общее решение исходного дифференциального уравнения.
- общее решение исходного дифференциального уравнения.