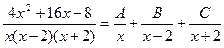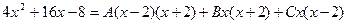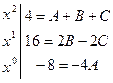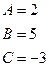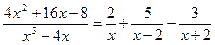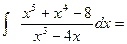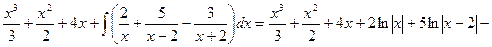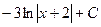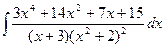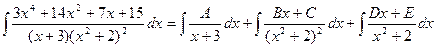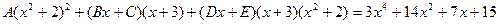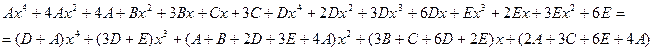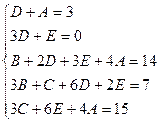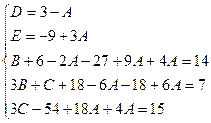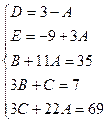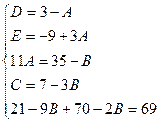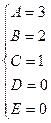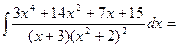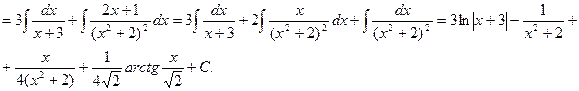Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислить неопределенные интегралыСодержание книги
Поиск на нашем сайте
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Интегрирование функций, содержащих квадратный трехчлен Интегрирование функций, содержащих квадратный трехчлен, сводится к выделению полного квадрата из квадратного трехчлена. Пример 1. Вычислить интеграл Решение. Выделим их квадратного трехчлена полный квадрат:
Пример 2. Вычислить интеграл Решение. Т.к.
Интегрирование рациональных дробей
Для того чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины. При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х. Алгоритм интегрирования рациональной дроби 1. Неправильную рациональную дробь представить в виде суммы целой части (многочлена) и правильной дроби. 2. Правильную дробь разложить на сумму простейших дробей со знаменателями, равными множителям знаменателя данной дроби. 3. Проинтегрировать полученную сумму многочлена и простейших дробей. Пример 2. Вычислить интеграл Решение. Правильную дробь
Пример 3. Вычислить интеграл Решение. Подынтегральная функция является неправильной дробью, поэтому сначала выделим её целую часть делением многочлена на многочлен:
Тогда Правильную дробь
Приведя правую часть равенства к общему знаменателю и отбросив знаменатель, получим:
Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений для нахождения коэффициентов A, B, C.
Таким образом, Подставив получившееся разложение в заданный интеграл, получим:
Пример 4. Вычислить интеграл Решение. Разложим подынтегральную функцию на простейшие дроби и найдем неопределенные коэффициенты.
Тогда значение заданного интеграла будет равно:
Практическое занятие №19 Наименование занятия: Интегрирование иррациональных функций. Универсальная подстановка Цель занятия: Научиться вычислять неопределенные интегралы от рациональных и иррациональных функций. Формировать ОК-1, ОК-2, ОК-3, ОК-4, ОК-5, ОК-6, ОК-7, овладеть знаниями и умениями, необходимыми для освоения ПК-1.1, ПК-1.2 (спец. 09.02.03), ПК-1.1, ПК-1.2 (спец. 09.02.04) Подготовка к занятию: Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной». Литература:
Задание на занятие:
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.108 (0.008 с.) |

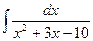
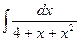
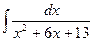
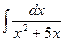
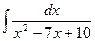
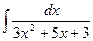
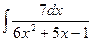
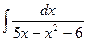
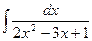
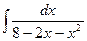
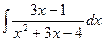
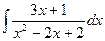
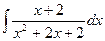
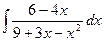
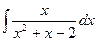
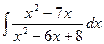
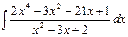
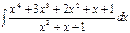
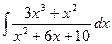
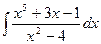
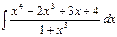
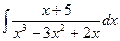
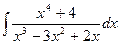
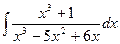
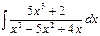
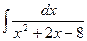
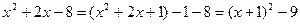 . Тогда
. Тогда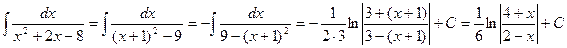
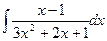
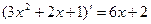 ,
, 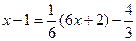 , то
, то 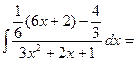
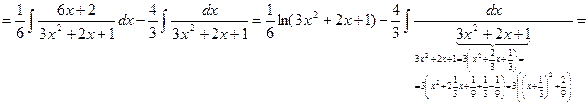
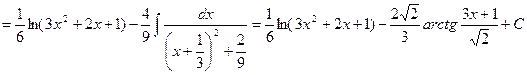
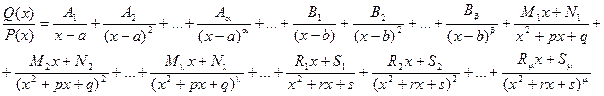
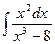
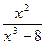 разложим на простейшие дроби.
разложим на простейшие дроби.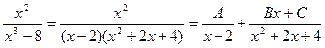
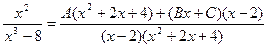
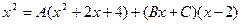
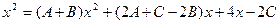


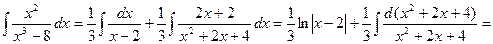
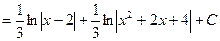
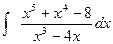 .
.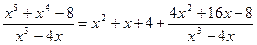 ;
;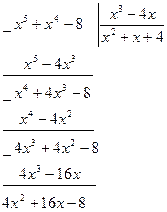
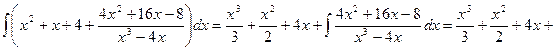
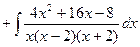
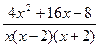 разложим на простейшие дроби и найдём коэффициенты A, B, C.
разложим на простейшие дроби и найдём коэффициенты A, B, C.