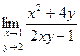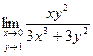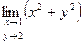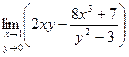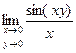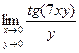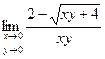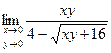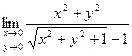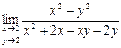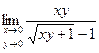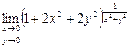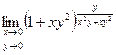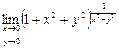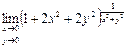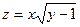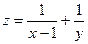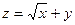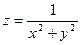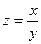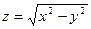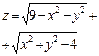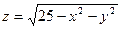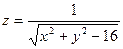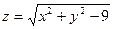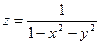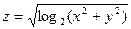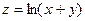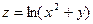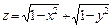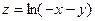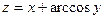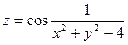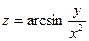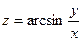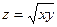Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление объема тела вращенияСодержание книги
Поиск на нашем сайте
Рассмотрим кривую, заданную уравнением y = f (x). Предположим, что функция f (x) непрерывна на отрезке [ a, b ]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси О х, то получим так называемое тело вращения, объем которого может быть легко найден по формуле:
Аналогично, объем тела вращения вокруг оси Оу криволинейной трапеции, ограниченной непрерывной кривой
Пример 2. Найти объем тела, образованного вращением вокруг оси Ох фигуры, одной полуволной синусоиды y = sin x и прямыми х = 0, х = π.
Решение. Применяя первую формулу для вычисления объема, получим:
Пример 3. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями:
Решение. Применим вторую формулу для вычисления объема.
Приложения определенного интеграла к решению физических задач
Схема применения определенного интеграла для вычисления некоторой величины u такова. Сначала нужно выразить некоторую переменную часть величины u в виде функции u (x) одного из ее параметров, который изменяется в известном из условия задачи интервале
Задача о нахождении пути, пройденного точкой Если υ = f (t) – скорость прямолинейно движущейся точки в момент времени t, то перемещение точки за промежуток времени [ a; b ] равно:
Пример 4. Скорость движения тела в момент времени t задается формулой υ = 15 – 3 t, где υ – скорость, м/с; t – время, с. Какой путь пройдет тело от начала отсчета времени до остановки?
Решение. Так как в момент остановки тела скорость его равна 0, то нужно определить путь, пройденный телом от момента времени t 1 = 0 до t 2 = 5 с. Подставив в формулу, получим
Задача о нахождении работы переменной силы Если переменная сила F (x) действует в направлении оси Ох, то работа силы на отрезке [ a; b ] равна
Пример 5. Какую работу нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 Н растягивает ее на 1 м?
Решение. Согласно закону Гука сила F, растягивающая пружину на х, равна F (x) = kx, где k – коэффициент пропорциональности. Полагая х = 0,01м и F (x) = 1 H, получим k = 100 и, следовательно, F (x) = 100 х. Подставим значения в формулу и найдем искомую работу:
Практическое занятие №22 Наименование занятия: Нахождение области определения и вычисление пределов для функций нескольких переменных Цель занятия: Научиться находить области определения и вычислять пределы для функций нескольких переменных. Формировать ОК-2, ОК-4, ОК-5. Подготовка к занятию: Повторить теоретический материал по теме «Функции нескольких переменных». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.103.185 (0.005 с.) |

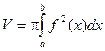
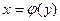 , осью ординат и двумя прямыми у = с, у = d, находится по формуле:
, осью ординат и двумя прямыми у = с, у = d, находится по формуле: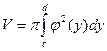
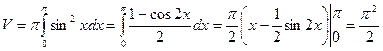
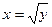 , у = 1, у = 4.
, у = 1, у = 4.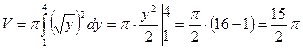
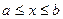 . Затем следует рассмотреть приращение ∆ u величины u (x), отвечающее изменению х на малую величину ∆х, и постараться найти для ∆ u приближенное выражение вида f (x) ∆х так, чтобы оно отличалось от ∆ u лишь на бесконечно малую величину. При этом следует пользоваться всеми возможными допущениями, которые в итоге сводятся к отбрасыванию бесконечно малых величин. Искомая величина u определяется интегрированием.
. Затем следует рассмотреть приращение ∆ u величины u (x), отвечающее изменению х на малую величину ∆х, и постараться найти для ∆ u приближенное выражение вида f (x) ∆х так, чтобы оно отличалось от ∆ u лишь на бесконечно малую величину. При этом следует пользоваться всеми возможными допущениями, которые в итоге сводятся к отбрасыванию бесконечно малых величин. Искомая величина u определяется интегрированием.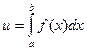
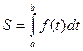
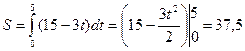 м.
м.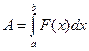
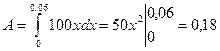 Дж.
Дж.