
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказать расходимость рядов, используя следствие из необходимого признака сходимости
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Понятие числового ряда Числовым рядом называется выражение вида:
При этом числа Примеры рядов Из членов бесконечной геометрической прогрессии можно составить ряд:
Если, например, взять a = 1, q =
Ряд
Сумма первых п членов ряда называется частичной суммой ряда. Таким образом, с рядом (1) связывается последовательность его частичных сумм S 1, S 2, …, Sn, …, где S 1 = а 1, S 2 = а 1 + а 2, … Sn = а 1 + а 2 + … + ап, … Ряд
Число S называется суммой ряда.
Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся. Например, ряд геометрической прогрессии
Гармонический ряд Свойства рядов Теорема 1. Если ряд
Другими словами: сходимость (расходимость) ряда не нарушится, если все его члены умножить на одно и то же отличное от нуля число. Теорема 2. Если ряды Другими словами: сходящиеся ряды можно почленно складывать и вычитать. Следствие: Сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд. Теорема 3. Если в ряде
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.109.201 (0.01 с.) |
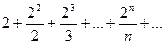
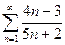
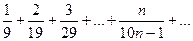
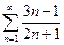
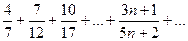
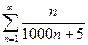
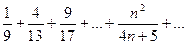
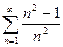
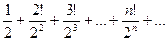
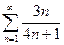
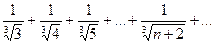
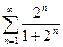
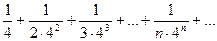
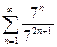
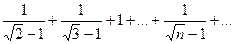
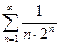
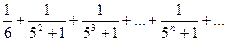
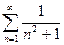
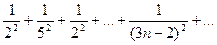
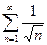
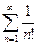
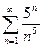
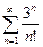
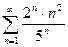
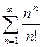
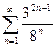
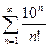
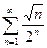
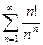
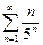
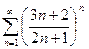
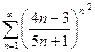
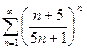
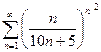
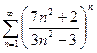
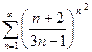
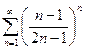
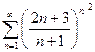
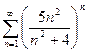
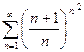
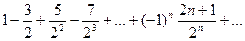
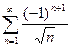
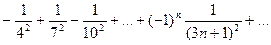
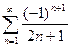
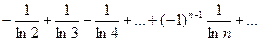
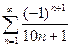
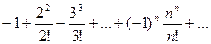
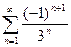
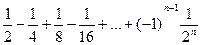
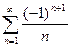
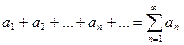 (1)
(1)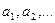 называются членами ряда (1), а n – общим членом ряда.
называются членами ряда (1), а n – общим членом ряда.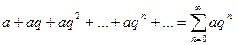 - ряд геометрической прогрессии
- ряд геометрической прогрессии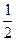 , то получим ряд:
, то получим ряд: 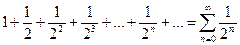
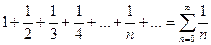 называется гармоническим рядом.
называется гармоническим рядом.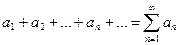 называется сходящимся, если сходится последовательность его частных сумм, т.е. если существует предел
называется сходящимся, если сходится последовательность его частных сумм, т.е. если существует предел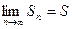 .
.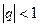 . Если
. Если 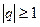 , то этот ряд сходится только при а = 0, а в остальных случаях расходится.
, то этот ряд сходится только при а = 0, а в остальных случаях расходится.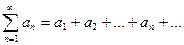 (1) сходится и его сумма равна S, то для произвольного числа с ряд
(1) сходится и его сумма равна S, то для произвольного числа с ряд 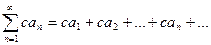 (2) тоже сходится, и его сумма равна сS. Если же ряд (1) расходится и с ≠ 0, то и ряд (2) расходится.
(2) тоже сходится, и его сумма равна сS. Если же ряд (1) расходится и с ≠ 0, то и ряд (2) расходится.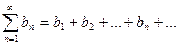 (3) сходятся и их суммы равны соответственно S1 и S3, то и каждый из двух рядов
(3) сходятся и их суммы равны соответственно S1 и S3, то и каждый из двух рядов 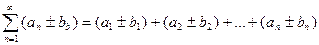 сходится и его сумма равна соответственно S1 ± S3.
сходится и его сумма равна соответственно S1 ± S3.


