Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных z = f(x, y) Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной. Областью определения функции z называется совокупность пар (х, у), при которых функция z существует. Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие Записывают:
Пример 1. Вычислить предел Решение. Воспользуемся повторным пределом функции двух переменных. Получим:
Пример 2. Найти область определения функции Решение. Данная функция имеет действительные значения, если Пример 3. Найти область существования функции Решение. Функция имеет действительные значения, если
Наименование занятия: Вычисление частных производных и дифференциалов функций нескольких переменных Цель занятия: Научиться находить частные производные и дифференциалы функций нескольких переменных. Формировать ОК-2, ОК-4, ОК-5. Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции нескольких действительных переменных». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.79.46 (0.009 с.) |

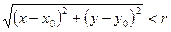 .
.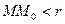 , также верно и условие
, также верно и условие 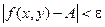 .
.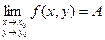
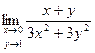
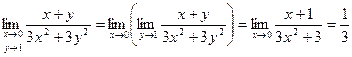
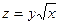 и изобразить ее на плоскости.
и изобразить ее на плоскости.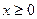 . Этому неравенству удовлетворяют все точки I и IV четверти. Область существования функции выглядит следующим образом:
. Этому неравенству удовлетворяют все точки I и IV четверти. Область существования функции выглядит следующим образом: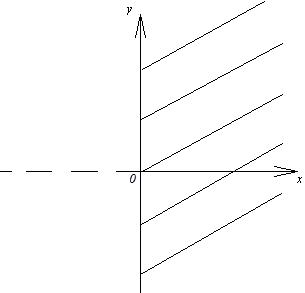
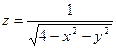
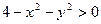 или
или 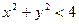 . Последнему неравенству удовлетворяют координаты точек, лежащих внутри окружности радиуса 2 с центром в начале координат. Область существования функции есть внутренность этого круга.
. Последнему неравенству удовлетворяют координаты точек, лежащих внутри окружности радиуса 2 с центром в начале координат. Область существования функции есть внутренность этого круга.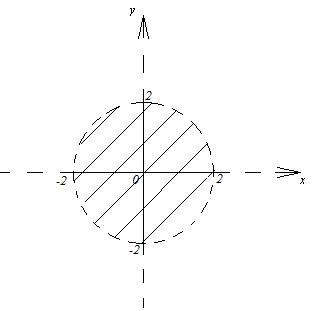
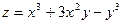
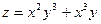
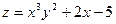
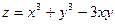
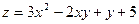
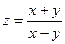
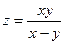
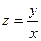
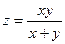
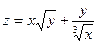
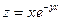
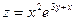
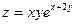
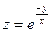
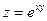
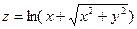
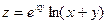
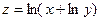
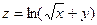
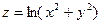
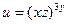
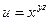
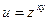
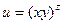
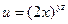
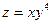
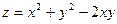
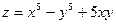
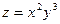
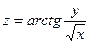
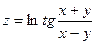
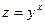
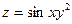
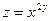
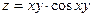
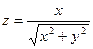
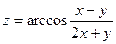
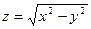
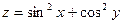
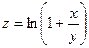
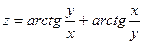

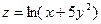
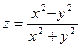
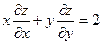 , если
, если 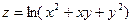
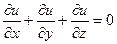 , если
, если 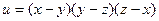
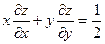 , если
, если 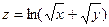
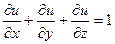 , если
, если 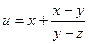
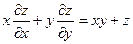 , если
, если