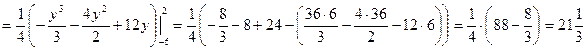Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление двойного интегралаСодержание книги
Поиск на нашем сайте Случай прямоугольной области Двойной интеграл по прямоугольной области
Пример 1. Вычислить двойной интеграл Решение. В соответствии с формулой (1) запишем
Затем вычисляем внешний интеграл по переменной х:
Таким образом,
Случай криволинейной области Если функция f(x, y) непрерывна в замкнутой области G, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и j £ y, тогда
Если функция f(x, y) непрерывна в замкнутой области G, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то
Пример 2. Вычислить интеграл Решение. Построим область G и вычислим интеграл по формуле (3)
4
G
0 2 x
Пример 3. Вычислить интеграл y = x, x = 0, y = 1, y = 2. Решение. Построим область G и вычислим интеграл по формуле (4)
y
y = x 2 G 1
0 x
Практическое занятие №25 Наименование занятия: Приложения двойных интегралов Цель занятия: Научиться применять двойные интегралы к вычислению площадей фигур. Формировать ОК-2, ОК-5. Подготовка к занятию: Повторить теоретический материал по теме «Интегральное исчисление функции нескольких действительных переменных». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие: Используя двойной интеграл, вычислить площади фигур, ограниченных линиями:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Геометрические приложения двойных интегралов Вычисление площадей в декартовых координатах
y = j(x) S
y = f(x) a b x
Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:
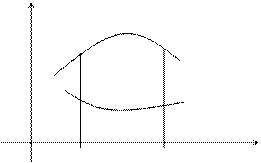
Пример 1. Вычислить площадь фигуры, ограниченной линиями y 2 = 4 x + 4; x + y – 2 = 0.
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от
S =
Практическое занятие №26 Наименование занятия: Решение дифференциальных уравнений
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |


 вычисляется по формулам:
вычисляется по формулам: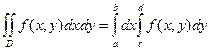 (1)
(1)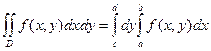 (2)
(2)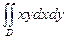 , где
, где 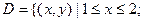

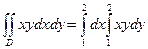 . Вычислим внутренний интеграл, считая переменную х постоянным числом:
. Вычислим внутренний интеграл, считая переменную х постоянным числом: .
.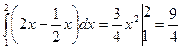 .
.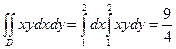
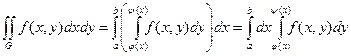 (3)
(3) (4)
(4)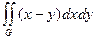 , если область G ограничена линиями: y = 0, y = x 2, x = 2.
, если область G ограничена линиями: y = 0, y = x 2, x = 2.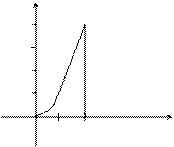 y
y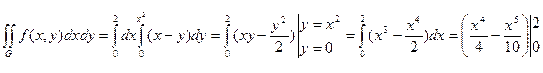 =
= 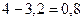
 , если область G ограничена линиями
, если область G ограничена линиями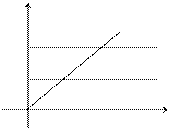

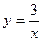 ,
,
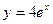 ,
у = 3,
у = 4
,
у = 3,
у = 4
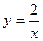 ,
,
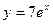 ,
у = 2,
у = 7
,
у = 2,
у = 7
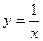 ,
,
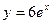 ,
у = 1,
у = 6
,
у = 1,
у = 6
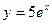 ,
у = 2,
у = 5
,
у = 2,
у = 5
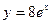 ,
у = 3,
у = 8
,
у = 3,
у = 8
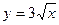 ,
,
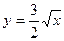 ,
,
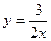 ,
х = 4
,
х = 4
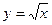 ,
,
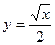 ,
, 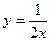 ,
х = 16
,
х = 16
 y
y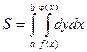

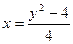 до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:
до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна: