
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислить определенные интегралыСодержание книги
Поиск на нашем сайте
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Приращение F (b) – F (a) любых из первообразных функций F (x) + С при изменении аргумента от х=а до х= b называется определенным интегралом от функции f. Вычисляется определенный интеграл по формуле Ньютона – Лейбница:
Свойства определенного интеграла 1) При перестановке пределов изменяется знак интеграла: 2) Интеграл с одинаковыми пределами равен нулю: 3) Отрезок интегрирования можно разбить на части: 4) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов 5) Постоянный множитель можно вынести за знак определенного интеграла.
Пример 1. Вычислить определенный интеграл Решение. Применяя формулу Ньютона-Лейбница и свойства определенного интеграла, получим:
Замена переменной в определенном интеграле Пусть задан интеграл Введем новую переменную в соответствии с формулой x = j (t). Тогда если 1) j (a) = а, j (b) = b 2) j (t) и j ¢(t) непрерывны на отрезке [ a, b ] 3) f (j (t)) определена на отрезке [ a, b ], то
Пример 2. Решение. Выполним замену (аналогично замене переменной в неопределенном интеграле): Введем новые переменные интегрирования. Полагая х = 0 и х = 4, подставим их в замену и получим t = 9 и t = 25. Следовательно,
Интегрирование по частям в определенном интеграле
Если функции u = j(x) и v = y(x) непрерывны на отрезке [ a, b ], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
Выбор u и dv осуществляется также как и в неопределенном интеграле. Пример 3. Решение. Выполним замену. Положим
Практическое занятие №21 Наименование занятия: Решение прикладных задач с помощью определенного интеграла Цель занятия: Научиться вычислять определенные интегралы, находить площади фигур, ограниченных линиями. Формировать ОК-1, ОК-2, ОК-3, ОК-4, ОК-5, ОК-6, ОК-7, овладеть знаниями и умениями, необходимыми для освоения ПК-1.1, ПК-1.2 (спец. 09.02.03), ПК-1.1, ПК-1.2 (спец. 09.02.04) Подготовка к занятию: Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной». Литература: Лобачева М.Е. Конспект лекций «Элементы высшей математики», 2010г. Задание на занятие: ВАРИАНТ 1 1. Вычислить работу, совершенную при сжатии пружины на 8 см, если для сжатия ее на 1 см нужно приложить силу в 10 Н.
2. Скорость движения точки меняется по закону v = 4 t – t 2, где v – скорость, м/с; t – время, с. Вычислить: путь, пройденный точкой за третью секунду движения; перемещение точки за первые 6 секунд движения.
3. Найти площадь фигуры, ограниченной линиями: 1) y = x ² – 8 x + 16; y = 6 – x 2) 3) у = х 2 – 2 (х ≥0), у = – 1, у = 7, х = 0
4. Найти объем тела, образованного вращением вокруг оси Оу кубической параболы
ВАРИАНТ 2 1. Вычислить работу, совершенную при растяжении пружины на 6 см, если длясжатия ее на 3 см нужно приложить силу 15 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v = 6 t ²– 4 t – 10, см/с. Вычислить: путь, пройденный точкой за первые 4 секунды движения; путь, пройденный точкой за четвертую секунду движения.
3. Найти площадь фигуры, ограниченной линиями: 1) y = x ² – 6 x + 9; 3 x – y – 9 = 0 2) 3) 4. Вычислить объем тела, полученного от вращения вокруг оси Ох трапеции, образованной прямыми
ВАРИАНТ 3 1. Вычислите работу, совершаемую при сжатии пружины на 0,05 м, если для ее сжатия на 0,02 м нужна сила в 10 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v = 3 t ² – 2 t – 1, м/c. Вычислить: путь, пройденный точкой за первые 3 секунды после начала движения; путь, пройденный точкой за третью секунду движения.
3. Найти площадь фигуры, ограниченной линиями: 1) y = – x ² + 6 х – 5, y = 0; 2) y 2 = x, y = x 2 3) у = 16х 3, у = 2, осью ординат 4. Вычислить объем тела, полученного от вращения вокруг оси Оу трапеции, образованной прямыми у = 3 х, у = 2, у = 4 и осью ординат
ВАРИАНТ 4 1. Вычислить работу, совершенную при сжатии пружины на 6 см, если для растяжения ее на 1 см нужно приложить силу в 10 Н.
2. Скорость точки, движущейся прямолинейно, задана уравнением v =24 t – 6 t ²¸ м/с. Вычислить: путь, пройденный точкой от начала движения до ее остановки; путь, пройденный точкой за вторую секунду движения.
3. Найти площадь фигуры, ограниченной линиями: 1) у = х 2 + 1, у = 2 х + 9, х = 0, у = 0 2) 3) x + 2 y - 8 = 0, у = 1, у = 3 4. Криволинейная трапеция, ограниченная гиперболой
ВАРИАНТ 5 1. Вычислить работу, которую нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 Н растягивает ее на 1 м.
2. Скорость движения точки меняется по закону v = 4 t – t 2, где v – скорость, м/с; t – время, с. Вычислить: путь, пройденный точкой за первые 3 секунды движения; путь, пройденный точкой от начала движения до ее остановки.
3. Найти площадь фигуры, ограниченной линиями: 1) y = x ² – 2 x + 3, y = x +3 2) у 3 = х, у = 1, х = 8 3) 4. Найти объем тела, полученного от вращения кривой Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.200.180 (0.007 с.) |

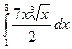
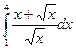
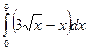
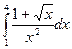
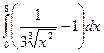
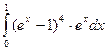
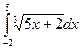
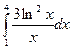
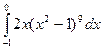
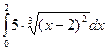
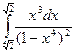
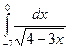
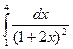
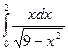
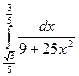
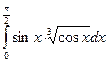
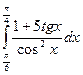
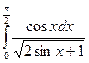
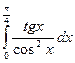
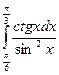
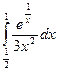
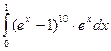
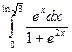
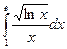
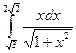
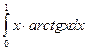
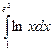
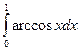
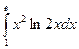
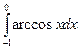
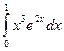
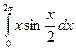
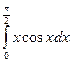
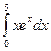
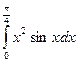
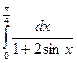
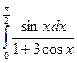
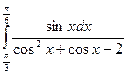
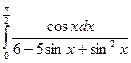
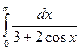
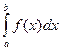 = F (b) – F (a)
= F (b) – F (a)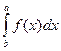
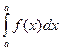 = 0
= 0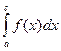 +
+ 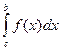
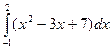
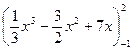 =
= 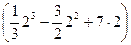 -
- 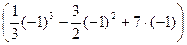 = 19,5
= 19,5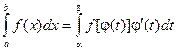
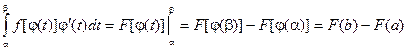
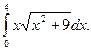
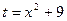 ;
; 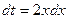 ;
; 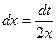 .
.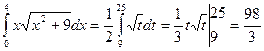
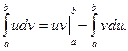
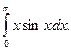
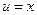 ,
, 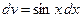 ; тогда
; тогда 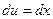 ,
, 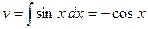 . Подставив в формулу интегрирования по частям, получим
. Подставив в формулу интегрирования по частям, получим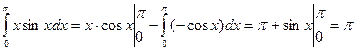 .
.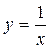 х = -3, х = – 1, осью абсцисс
х = -3, х = – 1, осью абсцисс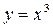 в пределах от у = 1 до у = 8
в пределах от у = 1 до у = 8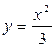 ,
, 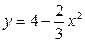
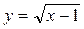 , у = 1, у = 0, х = 0
, у = 1, у = 0, х = 0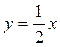 , х = 4, х = 6 и осью абсцисс
, х = 4, х = 6 и осью абсцисс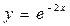 ,
, 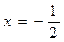 , х = 1
, х = 1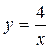 и прямыми х = 3, х = 12 вращается вокруг оси Ох. Найти объем тела вращения.
и прямыми х = 3, х = 12 вращается вокруг оси Ох. Найти объем тела вращения.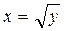 , у = 1, у = 4, осью ординат
, у = 1, у = 4, осью ординат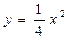 вокруг оси Оу в пределах от у = 1 до у = 5
вокруг оси Оу в пределах от у = 1 до у = 5


