
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарная работа системы сил контактного взаимодействия твердого тела со связями.
Положение твердого тела определяется вектором положения полюса
Элементарное перемещение тела определяется изменением положений всех его точек
Выберем в качестве полюса центр масс тела С. Элементарная работа всех дискретных сил взаимодействия
Здесь Если на векторы элементарного перемещения Силовое поле. Если в евклидовом пространстве R3 для каждого положения твердого тела задано поле потенциальной силы, зависящее от параметров, задающих положение точек тела, то говорят, что в пространстве (в теле) задано силовое поле. Элементарная работа силового поля силы тяжести твердого тела. Рассматриваем поле параллельных постоянных сил
Последнее слагаемое равно нулю по определению центра масс тела. Таким образом, искомая работа поля силы тяжести не зависит от поворота тела и определяется только перемещением центра масс. Работа и мощность системы сил твердого тела на действительном перемещении тела. В действительном движении твердого тела поле скоростей в теле задается формулой
а поле элементарных перемещений имеет вид
Тогда элементарная работа системы сил тела вычисляется по формуле
а мощность этих сил - по формуле
Аксиомы реакций связей.
Силы реакций перпендикулярны (направлены по нормали) к плоскостям (поверхностям).
При этом сила трения в покое тела не превосходит своего максимального значения (при движении) Нормальная часть реакции поверхности
Тело, соединенное шарниром с неподвижной опорой, может поворачиваться вокруг оси шарнира
5. Сферический шарнир. Рисунок 5.
6. Подпятник и подшипник. Рисунок 6. Сила реакции подпятника
Коэффициент сопротивления качению
Цилиндрический шарнир на подвижной опоре (в точке
Дифференциальный принцип механики. Рассматривается система N абсолютно твердых тел, на положения и, как следствие, на движение тел наложены геометрические (кинематические) ограничения (связи). Тела системы взаимодействуют между собой и с другими телами механической системы, не включенными в систему
Понятия и определения. Уравнения связей системы тел. Положение системы по отношению к инерциальной системе отсчета определяют 6 N скалярных параметров
а движение
Элементарные перемещения Несовместимые со связями элементарные перемещения Силы инерции твердого тела. Главный вектор и главный момент сил инерций тела. Поле элементарных сил инерций
по полю абсолютных ускорений При этом поле ускорений имеет вид:
Здесь Определение. Для тела вектор
есть главный вектор сил инерций, а вектор
есть главный момент сил инерций относительно центра масс С. Докажем, что в системе координат, связанной с телом, главный момент сил инерции вычисляется по формуле
Здесь Доказательство:
Если в теле есть неподвижная точка Силы взаимодействия тел механической системы подразделяют ся на активные силы Элементарная работа сил инерции твердого тела на виртуальных перемещении тела вычисляется так:
Здесь элементарное перемещение центра масс
Доказательство:
Если в теле есть неподвижная точка
где вектор
Если в плоском движении тела момент импульса
Здесь Если в теле имеется неподвижная ось вращения
Дифференциальный ПРИНЦИП механики систем с геометрическими (голономными) связями. При движении системы
Принцип (аксиома) применим для любого количества Дифференциальный принцип механики на виртуальных перемещениях: принцип Даламбера – Лагранжа. Дифференциальный принцип механики на Возможных (виртуальных) перемещениях применяют для нахождения движения системы. Принцип дает возможность написать дифференциальные уравнения движения системы в случаях, когда элементарная работа всех сил контактного взаимодействия системы равна нулю:
В таком случае говорят, то есть при идеальных связях. В этом случае из дифференциального принципа следует, что сумма элементарных работ всех активных сил и всех сил инерций системы равна нулю на любых виртуальных перемещениях системы:
Эту форму дифференциального принципа называют принцип Даламбера - Лагранжа. Используя уравнения связей, вектор положения точек тела Поэтому принцип Даламбера - Лагранжа можно представить в следующем виде:
где В силу независимости и произвольности виртуальных перемещений
Эти уравнения есть дифференциальные уравнения движения системы тел с идеальными связями в обобщенных координатах. Они не включают неизвестные силы контактных взаимодействий. Для системы
Консервативнаясистема. Положения равновесия консервативных систем. Консервативная система имеет геометрические стационарные связи, сумма элементарных работ сил реакций идеальных связей равна нулю, а все работающие силы потенциальны. Положения равновесия определяются свойствами сил взаимодействий и виртуальными перемещениями в этих положениях. А именно: в каждом положении равновесия равны нулю виртуальные работы силового поля и сил реакций связей на любых виртуальных перемещениях:
Это свойство сил взаимодействий примем за определение положений равновесия. Так как для потенциальных сил в положениях равновесия виртуальную работу активных сил можно выразить через дифференциал потенциальной энергии, то есть
то равенство нулю полного дифференциала Следующее определение положений равновесия консервативной системы тождественно предыдущему. Положениями равновесия консервативной системы с идеальными связями называются такие положения системы
Это определение не связано с движениями системы, и, таким образом, не зависит от начальных состояний системы (начальных положений и начальных скоростей тел).
Пример 1. Математический маятник: материальная точка М движется по части окружности Заметим, что на границе интервала виртуальная работа силы тяжести (и силы инерции) не равны нулю, поэтому граница интервала не есть положение равновесия, хотя потенциальная энергия маятника в ней имеет максимум.
Дифференциальный принцип механики для систем в положениях равновесия, состоянии равновесия и в покое. Если механическая система с идеальными связями находится в покое на конечном интервале времени, то равны нулю все силы инерции. Тогда
Используя обобщенные координаты системы и их вариации где
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.242.165 (0.071 с.) |
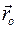 и собственной ортогональной матрицей
и собственной ортогональной матрицей  ориентации подвижного базиса по отношению к неподвижному базису. Положение любой точки
ориентации подвижного базиса по отношению к неподвижному базису. Положение любой точки 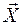 в теле по отношению к центру масс задается в неподвижном пространстве вектором
в теле по отношению к центру масс задается в неподвижном пространстве вектором 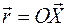 . Тогда положение точки
. Тогда положение точки 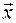 :
: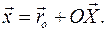
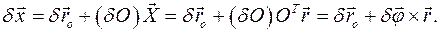
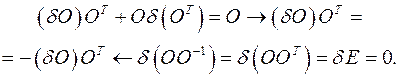
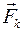 твердого тела, любая точка на линиях действия которых определяются векторами
твердого тела, любая точка на линиях действия которых определяются векторами 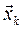 , а их элементарные перемещения - векторами
, а их элементарные перемещения - векторами 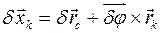 , равна:
, равна: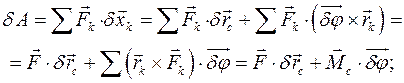
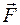 есть главный вектор всех действующих на тело сил, а
есть главный вектор всех действующих на тело сил, а 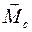 есть главный момент этих сил относительно центра масс.
есть главный момент этих сил относительно центра масс.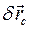 и элементарного поворота тела
и элементарного поворота тела 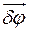 наложены связи, то число независимых элементарных перемещений меньше шести. В этом случае элементарную работу можно выразить через независимые элементарные перемещения
наложены связи, то число независимых элементарных перемещений меньше шести. В этом случае элементарную работу можно выразить через независимые элементарные перемещения 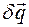 .
.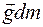 в каждой точке тела. Элементарную работу поля ищем на элементарном перемещении
в каждой точке тела. Элементарную работу поля ищем на элементарном перемещении 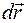
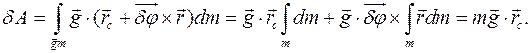
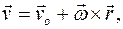
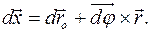
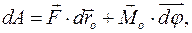
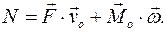
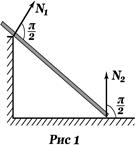 1. Гладкая плоскость, поверхность, гладкая опора. Рисунок 1.
1. Гладкая плоскость, поверхность, гладкая опора. Рисунок 1.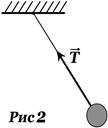 2. Невесомая нерастяжимая нить. Рисунок 2. Сила реакции нити
2. Невесомая нерастяжимая нить. Рисунок 2. Сила реакции нити 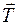 направлена вдоль нити от тела.
направлена вдоль нити от тела. 3. Поступательное (без вращения) скольжение тела по гладкой (без трения) поверхности (плоскости).
3. Поступательное (без вращения) скольжение тела по гладкой (без трения) поверхности (плоскости).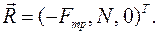
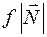 :
: 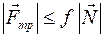 .
.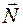 перпендикулярна к поверхности. Коэффициент трения скольжения
перпендикулярна к поверхности. Коэффициент трения скольжения 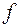 не имеет азмерности.
не имеет азмерности. 4. Цилиндрический шарнир, соединяющий тело с неподвижной опорой. Рисунок 4.
4. Цилиндрический шарнир, соединяющий тело с неподвижной опорой. Рисунок 4. При отсутствии трения и скольжения тела вдоль оси, а также при плоской нагрузке на тело сила реакции оси шарнира имеет неизвестную величину и неизвестное направление в плоскости, перпендикулярной к оси шарнира:
При отсутствии трения и скольжения тела вдоль оси, а также при плоской нагрузке на тело сила реакции оси шарнира имеет неизвестную величину и неизвестное направление в плоскости, перпендикулярной к оси шарнира: 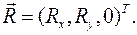
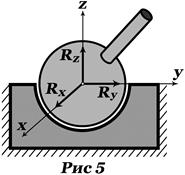 Цилиндрический (подвижный) шарнир может связывать два подвижных тела. Аксиома реакции связи при этом не изменяется.
Цилиндрический (подвижный) шарнир может связывать два подвижных тела. Аксиома реакции связи при этом не изменяется.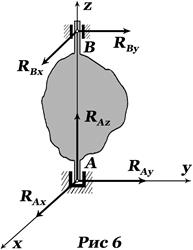 Реакция опоры шарнира на тело, соединенное с шаровой частью шарнира, при произвольной нагрузке на тело может иметь любое направление в пространстве. Поэтому
Реакция опоры шарнира на тело, соединенное с шаровой частью шарнира, при произвольной нагрузке на тело может иметь любое направление в пространстве. Поэтому 
 может иметь произвольное направление. Реакция подшипника
может иметь произвольное направление. Реакция подшипника  перпендикулярна к оси
перпендикулярна к оси 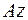 :
: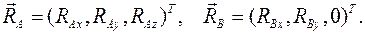
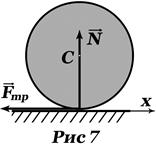 7. Качение цилиндра (без скольжения). Рисунок 7. Касание цилиндра с плоскостью происходит в одной точке. Сила трения не связана с нормальной реакцией и зависит от движения тела.
7. Качение цилиндра (без скольжения). Рисунок 7. Касание цилиндра с плоскостью происходит в одной точке. Сила трения не связана с нормальной реакцией и зависит от движения тела.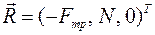
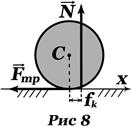 8. Качение цилиндра (без скольжения) при наличии момента сопротивления качению. Рисунок 8. Касание цилиндра с плоскостью происходит не в одной точке. Главный вектор сил реакций
8. Качение цилиндра (без скольжения) при наличии момента сопротивления качению. Рисунок 8. Касание цилиндра с плоскостью происходит не в одной точке. Главный вектор сил реакций 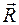 и главный момент сил реакций
и главный момент сил реакций 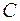 равен
равен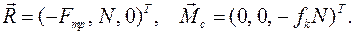
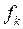 имеет размерность длины (метр).
имеет размерность длины (метр).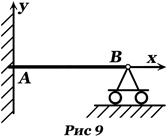 9. Реакция балки, заделанной в стену. Рисунок 9. При нагрузке на балку в плоскости
9. Реакция балки, заделанной в стену. Рисунок 9. При нагрузке на балку в плоскости 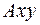 реакция стены определяется главным вектором заделки
реакция стены определяется главным вектором заделки 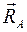 и главным моментом заделки
и главным моментом заделки 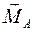 :
: 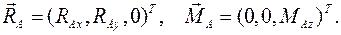
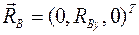 .
.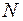 тел.
тел.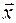 (координаты, углы),
(координаты, углы), 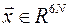 . Положение
. Положение 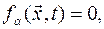
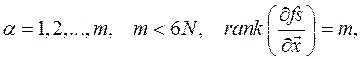
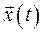 удовлетворяет еще и кинематическим уравнениям связей, полученным из уравнений связи дифференцированием их по времени один и два раза. Скалярные функции векторного аргумента
удовлетворяет еще и кинематическим уравнениям связей, полученным из уравнений связи дифференцированием их по времени один и два раза. Скалярные функции векторного аргумента 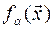 дважды непрерывно дифференцируемы по времени, а функционально независимые уравнения связей для любого момента времени позволяют выбрать
дважды непрерывно дифференцируемы по времени, а функционально независимые уравнения связей для любого момента времени позволяют выбрать 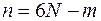 независимых элементарных перемещений
независимых элементарных перемещений 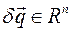 из уравнений связей в вариациях
из уравнений связей в вариациях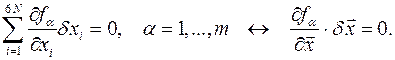
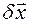 называются возможными (виртуальными) перемещениями, а скалярные параметры (координаты и углы)
называются возможными (виртуальными) перемещениями, а скалярные параметры (координаты и углы) 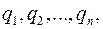 которые соответствуют, независимым из них
которые соответствуют, независимым из них 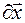 системы тел произвольны, независимы и не удовлетворяют уравнениям связей.
системы тел произвольны, независимы и не удовлетворяют уравнениям связей. 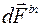 твердого тела определим по Даламберу
твердого тела определим по Даламберу 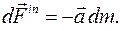
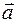 всех его элементарных масс
всех его элементарных масс 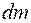 , положение которых по отношению к центру масс С задается векторами
, положение которых по отношению к центру масс С задается векторами 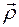 .
.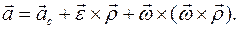
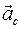 есть абсолютное ускорение центра масс тела,
есть абсолютное ускорение центра масс тела, 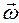 есть абсолютная угловая скорость, а
есть абсолютная угловая скорость, а 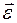 есть абсолютное угловое ускорение тела. В системе координат, связанной с телом, векторы
есть абсолютное угловое ускорение тела. В системе координат, связанной с телом, векторы 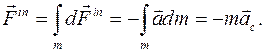
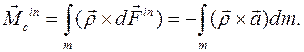
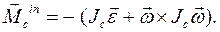
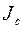 есть оператор инерции тела относительно осей координат, связанных с телом, с началом в центре масс С. Элементы его матрицы
есть оператор инерции тела относительно осей координат, связанных с телом, с началом в центре масс С. Элементы его матрицы 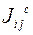 постоянны.
постоянны.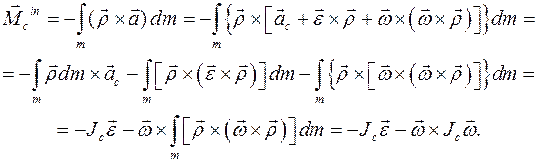
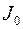 относительно неподвижной точки.
относительно неподвижной точки.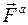 бесконтактного взаимодействия тел и силы контактного взаимодействия
бесконтактного взаимодействия тел и силы контактного взаимодействия 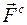 (акции и реакции). Добавим к ним для каждого тела силы инерции
(акции и реакции). Добавим к ним для каждого тела силы инерции 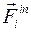 и вычислим их элементарную работу.
и вычислим их элементарную работу.
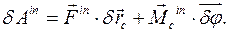
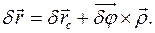
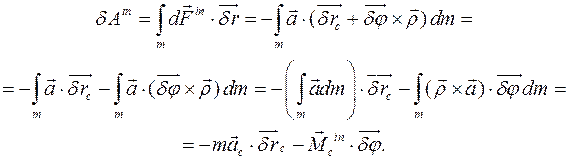
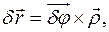
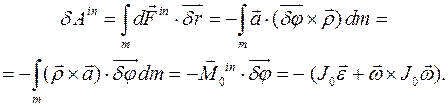
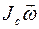 тела параллелен вектору угловой скорости
тела параллелен вектору угловой скорости 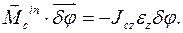
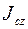 есть осевой момент инерции тела относительно оси
есть осевой момент инерции тела относительно оси 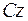 . Для этого необходимо, чтобы эта ось была главной осью оператора инерции тела.
. Для этого необходимо, чтобы эта ось была главной осью оператора инерции тела. , проходящая через некоторую точку
, проходящая через некоторую точку 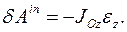
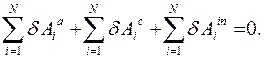
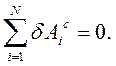
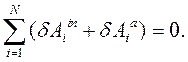
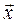 и его вариацию
и его вариацию 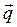 и их виртуальные перемещения
и их виртуальные перемещения 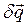 .
. 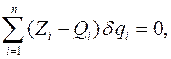
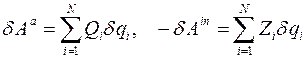 .
.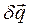 , уравнение дифференциального принципа распадаются на n уравнений
, уравнение дифференциального принципа распадаются на n уравнений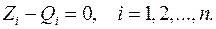
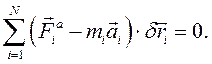
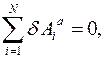
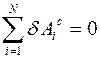 .
.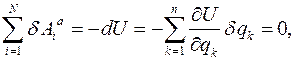
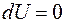 потенциальной энергии
потенциальной энергии 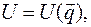
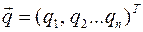 , означает, что положения равновесия доставляют экстремум потенциальной энергии.
, означает, что положения равновесия доставляют экстремум потенциальной энергии.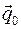 , совместимые со связями, в которых потенциальная энергия системы U принимает экстремальные значения:
, совместимые со связями, в которых потенциальная энергия системы U принимает экстремальные значения: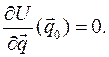
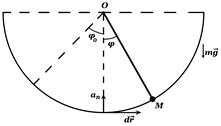 Так как связи системы идеальны, то из принципа Даламбера – Лагранжа следует, что на движениях системы в положениях равновесия равна нулю и виртуальная работа сил инерций.
Так как связи системы идеальны, то из принципа Даламбера – Лагранжа следует, что на движениях системы в положениях равновесия равна нулю и виртуальная работа сил инерций. в вертикальной плоскости. В нижней точке,
в вертикальной плоскости. В нижней точке,  , равны нулю виртуальные работы силы тяжести и силы реакции нити. Это есть положение равновесия. маятника. Так как скорость точки в положении равновесия имеет максимум, то касательное ускорение в нем равно нулю. Поэтому сила инерции точки, определяемая нормальным ускорением, перпендикулярна виртуальному перемещению и не работает на нем.
, равны нулю виртуальные работы силы тяжести и силы реакции нити. Это есть положение равновесия. маятника. Так как скорость точки в положении равновесия имеет максимум, то касательное ускорение в нем равно нулю. Поэтому сила инерции точки, определяемая нормальным ускорением, перпендикулярна виртуальному перемещению и не работает на нем.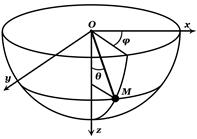 Пример 2. Сферический маятник: материальная точка подвешена на нити в точке О, центре сферы. Хотя сила тяжести и сила реакции нити не работают на элементарных перемещениях, векторы которых являются касательными векторами к параллелям сферы, однако они работают на виртуальных перемещениях, касательных к меридианам сферы. В нижней точке сферы эти силы не работают на всех виртуальных перемещениях, поэтому нижняя точка сферы есть положение равновесия маятника.
Пример 2. Сферический маятник: материальная точка подвешена на нити в точке О, центре сферы. Хотя сила тяжести и сила реакции нити не работают на элементарных перемещениях, векторы которых являются касательными векторами к параллелям сферы, однако они работают на виртуальных перемещениях, касательных к меридианам сферы. В нижней точке сферы эти силы не работают на всех виртуальных перемещениях, поэтому нижняя точка сферы есть положение равновесия маятника.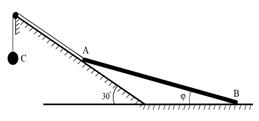 Пример 3. Система состоит из однородного тонкого стержня АВ с массой М и груза D с массой
Пример 3. Система состоит из однородного тонкого стержня АВ с массой М и груза D с массой 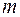 , соединенного со стержнем невесомой нитью. При гладкости плоскостей консервативная система с одной степенью свободы имеет идеальные связи. При произвольных массах тел в системе нет положений равновесия. Но если
, соединенного со стержнем невесомой нитью. При гладкости плоскостей консервативная система с одной степенью свободы имеет идеальные связи. При произвольных массах тел в системе нет положений равновесия. Но если 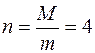 , то все положения системы, допустимые связями
, то все положения системы, допустимые связями 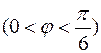 , есть безразличные положения равновесия. Это видно из принципа виртуальных перемещений, который можно записать в следующем виде:
, есть безразличные положения равновесия. Это видно из принципа виртуальных перемещений, который можно записать в следующем виде: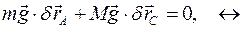
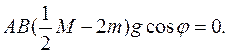

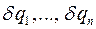 , принцип виртуальных перемещений можно записать в следующем виде:
, принцип виртуальных перемещений можно записать в следующем виде: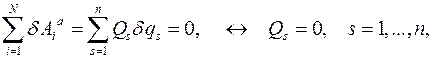
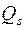 есть обобщенные силы системы.
есть обобщенные силы системы.


