
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции Гамильтона и Раусса. Уравнения Гамильтона и Раусса.
Введем функцию Лагранжа
то
где
мы выражаем ее через новые переменные Определение. Функция
В частности, для консервативной системы функция Лагранжа имеет следующий вид:
Из системы линейных уравнений Канонические уравнения Гамильтона В силу известных свойств преобразования Лежандра имеем:
а из уравнений Лагранжа второго рода имеем
Тогда в переменных Гамильтона
Уравнения Раусса. Выберем теперь в качестве независимых переменных K обобщенных координат и обобщенных скоростей
Определение. Функцией Рауса R называется преобразование Лежандра (со знаком минус) функции Лагранжа L по части обобщенных скоростей
В переменных Раусса дифференциальные уравнения движения запишем в виде, который называется уравнениями Раусса:
Доказательство. По свойству преобразования Лежандра имеем
а по определению преобразования Лежандра и его свойству, а также по свойству двойного преобразования Лежандра имеет место
Наконец, из уравнения Лагранжа
Следует
В результате, уравнения Раусса запишутся в виде. Решение уравнений Раусса для систем с циклическими координатами. Пусть теперь механическая система с n степенями свободы имеет циклические координаты
тогда как остальные координаты
Если выполняется условие
то из системы уравнений
можно найти Зависимость позиционных координат от времени и начальных условий находят из первых уравнений Раусса
после чего из оставшихся уравнений ищут зависимость от времени позиционных координат.
Устойчивость движений консервативных в окрестности их положений равновесия. Понятие устойчивости движений. Изучается устойчивость некоторого множества решений Определение. Решение уравнений движения консервативной системы
Устойчивое решение называется асимптотически устойчивым, если
Далее для решения некоторых задач по устойчивости движений голономных систем будут использоваться достаточные условия устойчивости некоторых классов движений. Достаточные условия устойчивости локальных положений равновесия консервативных систем. Теорема Дирихле – Лагранжа. Пусть в консервативной системе нет циклических координат и существуют локальные (изолированные) положения равновесия, которые можно найти из условий экстремальности потенциальной энергии
Теорема Дирихле - Лагранжа. Если в положении равновесия Минимум потенциальной энергии U в положении равновесия Достаточные условия частичной устойчивости положений равновесия консервативных систем с циклическими координатами.
Теорема. Если в положении равновесия потенциальная энергия консервативной системы имеет локальный минимум по позиционным координатам, то положение равновесия частично устойчиво по позиционным координатам и скоростям. Положение равновесия систем с циклической координатой неустойчиво по Ляпунову.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.167 (0.007 с.) |
 =
=  , записанную в переменных Лагранжа, Так как для консервативной и обобщенно консервативной систем в кинетической энергии системы имеется квадратичная функция обобщенных скоростей
, записанную в переменных Лагранжа, Так как для консервативной и обобщенно консервативной систем в кинетической энергии системы имеется квадратичная функция обобщенных скоростей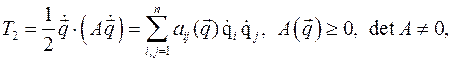
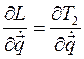 линейно зависит от обобщенных скоростей. Применим к функции Лагранжа преобразование Лежандра по обобщенным скоростям:
линейно зависит от обобщенных скоростей. Применим к функции Лагранжа преобразование Лежандра по обобщенным скоростям: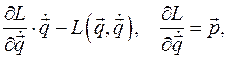
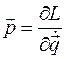 есть обобщенный импульс. Так как матрица A положительно определена, из этой системы линейных уравнений относительно обобщенных скоростей выразим обобщенные скорости через обобщенные импульсы и обобщенные координаты. В результате, подставляя обобщенные скорости в функцию
есть обобщенный импульс. Так как матрица A положительно определена, из этой системы линейных уравнений относительно обобщенных скоростей выразим обобщенные скорости через обобщенные импульсы и обобщенные координаты. В результате, подставляя обобщенные скорости в функцию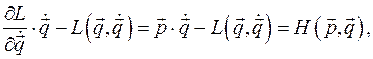
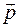 ,
,  , которые называются переменными Гамильтона.
, которые называются переменными Гамильтона. результат преобразования Лежандра функции Лагранжа по обобщенным скоростям
результат преобразования Лежандра функции Лагранжа по обобщенным скоростям 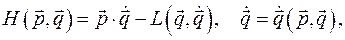

 обобщенные скорости выражаются просто:
обобщенные скорости выражаются просто:  .
.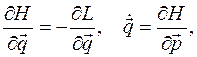

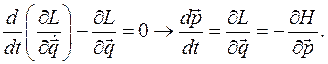
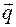 канонические уравнения Гамильтона запишутся так:
канонические уравнения Гамильтона запишутся так: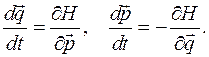
 (их обозначение общего члена есть
(их обозначение общего члена есть  ) и n - k переменных
) и n - k переменных  (их общий член обозначим
(их общий член обозначим 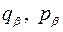 ).
). 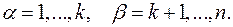
 :
: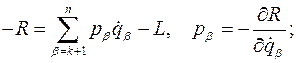
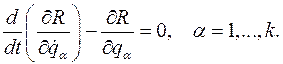
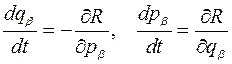



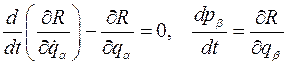
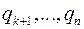 (их общее обозначение
(их общее обозначение 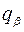 )
)
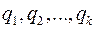 (позиционные координаты, их общее обозначение
(позиционные координаты, их общее обозначение  ) содержатся в функции Лагранжа
) содержатся в функции Лагранжа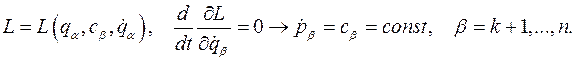
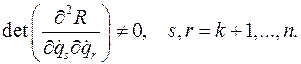
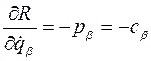
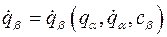 .
.
 уравнений движения консервативных систем, для которых начальные условия
уравнений движения консервативных систем, для которых начальные условия  находятся в малой окрестности некоторого положения равновесия системы, то есть
находятся в малой окрестности некоторого положения равновесия системы, то есть 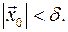


 в положении равновесия:
в положении равновесия: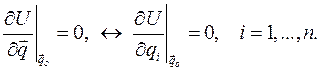
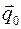 потенциальная энергия консервативной системы имеет локальный минимум, то положение равновесия устойчиво по Ляпунову (по обобщенным координатам и скоростям).
потенциальная энергия консервативной системы имеет локальный минимум, то положение равновесия устойчиво по Ляпунову (по обобщенным координатам и скоростям).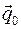 определяется положительной определенностью матрицы из коэффициентов второго дифференциала потенциальной энергии
определяется положительной определенностью матрицы из коэффициентов второго дифференциала потенциальной энергии 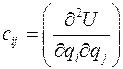 . Часто критерия Сильвестра достаточно, чтобы проверить положительную определенность матрицы С: все главные миноры матрицы должны быть положительны.
. Часто критерия Сильвестра достаточно, чтобы проверить положительную определенность матрицы С: все главные миноры матрицы должны быть положительны.


