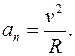Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение твердого тела вокруг неподвижной оси.
Матрица вращения
откуда вектор угловой скорости
Во вращении твердого тела вокруг неподвижной оси вектор угловой скорости параллелен оси вращения Скорости точек тела перпендикулярны к оси вращения и к вектору Скорость любой точки тела можно представить в следующем виде:
Плоское движение твердого тела. Скорость полюса Плоское движение есть композиция поступательного и вращательного движений. Для двух точек А и В плоской фигуры тела скорости точек лежат в плоскости фигуры, а угловая скорость ей перпендикулярна. Плоское движение имеет три степени свободы. Скорости любых двух точек тела связаны соотношением:
Мгновенный центр скоростей (мгновенная ось вращения) в плоском движении тела. Для непоступательного плоского движения твердого тела в любом положении тела существует точка Р плоской фигуры (или ее продолжения), скорость которой равна нулю. Эта точка называется мгновенный центр скоростей плоской фигуры. Взяв её за полюс, и зная, что скорость полюса равна нулю, получим, что скорость любой точки А плоской фигуры перпендикулярна вектору
Эта формула задает поле скоростей точек твердого тела в плоском движении. Ось, перпендикулярную плоскости фигуры и проходящую через мгновенный центр скоростей, называют мгновенной осью вращения. Таким образом, непоступательное плоское движение тела можно представить, в каждом положении тела, как только вращательное. Сферическое движение тела. В этом движении имеется одна неподвижная точка в теле О. Поэтому
Мгновенная ось вращения, если может быть найдена, проходит в этом случае через неподвижную точку.
Ускорение точек твердого тела. Угловое ускорение тела. Продифференцируем по времени формулу для поля скоростей:
Здесь вектор
Эта формула задает п оле ускорений в теле, то есть каждому вектору В случаях плоского и вращательного движений ускорение любой точки тела вычисляется по формуле:
где вектор Криволинейные координаты. Положение точки тела можно задавать не только тремя декартовыми координатами, но и другими упорядоченными тройками скалярных параметров, взаимно однозначно и непрерывно связанных с декартовыми координатами. Определение. Каждой точке
Назовем
Определение. Три вектора называются базисом криволинейных координат в точке Компоненты векторов базиса записаны в декартовом базисе. Векторы базиса изменяются при изменении положения точки
Длины
Каждый вектор базиса касается соответствующей координатной линии, вдоль которой изменяется только одна координата, а две другие фиксированы. Например, первая координатная линия запишется так: В криволинейной системе координат в каждой точке Определение. Поверхности уровня функций
называются координатными поверхностями, проходящими через точку Определение. Три вектора градиентов к соответствующим координатным поверхностям
называются векторами кобазиса в точке Изменение векторов базиса при изменении положения точки
В последнем выражении опущен знак суммирования по паре индексов суммирования Далее при написании формул будет использоваться правило Эйнштейна.
Коэффициенты
Поэтому число различных символов Кристоффеля меньше двадцати семи. Можно показать, что векторы базиса и кобазиса взаимны, то есть их скалярные произведения равны символу Кронекера:
Символы Кристоффеля вычисляются следующим образом:
Векторы базиса Определение. Криволинейная система координат называется ортогональной системой координат, если векторы базиса ортогональны:
В этом случае вводится ортонормированный базис
Можно показать, что для ортогональных криволинейных координат нормированные векторы базиса и кобазиса совпадают. Скорость и ускорение точки тела в криволинейных координатах. Определение. Движение точки в криволинейных координатах записывается следующим образом:
Скорость и ускорение точки в базисе криволинейных координат:
Компоненты называются контравариантными компонентами векторов скорости и ускорения соответственно. Компоненты В последних формулах применяется следующее правило (Эйнштейна): если в одной части уравнения, (формулы), индекс свободный, то есть по нему нет суммирования, то по нему нет суммирования и в другой части уравнения. Физические компоненты векторов скорости Цилиндрическая ортогональная система координат,
Обратное отображение
Коэффициенты Ламе: Базис
Очевидно, что эти векторы взаимно ортогональны. Кобазис
Ненулевые символы Кристоффеля: Физические компоненты вектор ов скорости и ускорения имеют вид:
Полярная система координат. Если в цилиндрических координатах положить z = 0, то система координат называется полярной системой координат. Она описывает движение точки в одной плоскости. Для нее физические компоненты скорости и ускорения имеют вид
Прямое отображение
Обратное отображение
Коэффициенты Ламе: Векторы базиса и кобазиса связаны следующим образом:
Символы Кристоффеля имеют следующие значения:
Связь контравариантных и физических компонент скорости и ускорения имеет вид:
Вычислим третью физическую компоненту вектора ускорения:
Окончательно, физические компоненты векторов скорости и ускорения в сферических координатах вычисляются по следующим формулам:
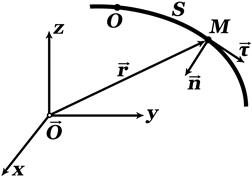
Движение точки вдоль траектории. Скорость и ускорение точки в проекциях на естественный ортонормированный базис. Траектория какой-либо точки тела есть геометрическое место всех последовательных положений точки при движении тела. Принимаем, что это есть некоторая гладкая кривая линия в Пусть движение точки тела (далее точки) задано в декартовых координатах:
Выберем на кривой начало отсчета О дуговой координаты s точки М при ее движении как расстояние вдоль кривой от начального положения (точки О) до ее текущего положения М:
Касательный к траектории вектор
Вектор главной нормали
Величина В каждой точке траектории три единичных вектора Движение точки в естественной форме
Скорость точки
а её проекция на ось
Ускорение точки
Они называются так: касательное
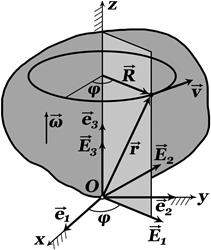
Если траектория точки есть окружность с радиусом R, то кривизна окружности равна, по определению, радиусу окружности, и поэтому нормальное ускорение точки есть
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.126.74 (0.064 с.) |
 В теле имеется две неподвижные точки. Тогда все точки оси
В теле имеется две неподвижные точки. Тогда все точки оси  , проходящей через эти точки, неподвижны. Нет поступательного движения, а вращательное движение задается одним параметром – углом поворота
, проходящей через эти точки, неподвижны. Нет поступательного движения, а вращательное движение задается одним параметром – углом поворота 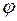 подвижных векторов базиса и вокруг неподвижной оси
подвижных векторов базиса и вокруг неподвижной оси 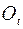 выражается через угол
выражается через угол 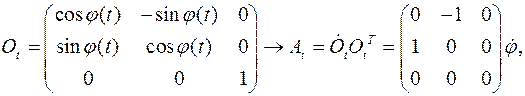
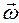 имеет в неподвижном базисе одну ненулевую компоненту
имеет в неподвижном базисе одну ненулевую компоненту 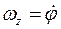 :
: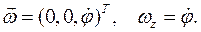
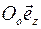 (по определению).
(по определению).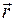 . Точки тела движутся по окружностям с радиусами R, равными расстоянию точек от оси вращения и имеют величину
. Точки тела движутся по окружностям с радиусами R, равными расстоянию точек от оси вращения и имеют величину 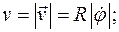
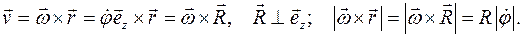
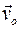 расположена в одной и той же неподвижной плоскости
расположена в одной и той же неподвижной плоскости 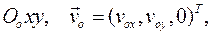 а угловая скорость перпендикулярна плоскости:
а угловая скорость перпендикулярна плоскости: 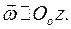
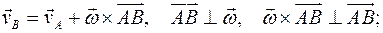
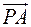 :
: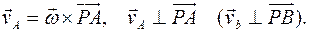
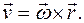
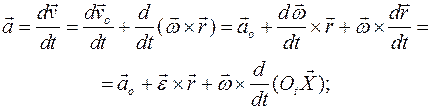
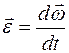 называется угловым ускорением твердого тела. Итак,
называется угловым ускорением твердого тела. Итак,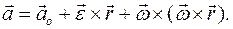
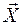 сопоставляется вектор ускорения точки
сопоставляется вектор ускорения точки 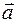 .
.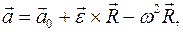
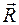 перпендикулярен векторам
перпендикулярен векторам 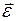 .
.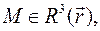 с координатами
с координатами 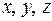 сопоставим три упорядоченных числа
сопоставим три упорядоченных числа 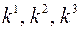 по некоторому правилу:
по некоторому правилу: 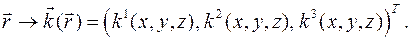
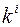 , i = 1, 2, 3, криволинейными координатами точки М. Функции
, i = 1, 2, 3, криволинейными координатами точки М. Функции 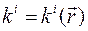 взаимно однозначны и непрерывно дифференцируемы по всем координатам и имеют обратные функции в некоторой области взаимной однозначности
взаимно однозначны и непрерывно дифференцируемы по всем координатам и имеют обратные функции в некоторой области взаимной однозначности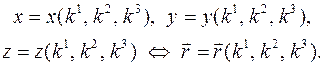
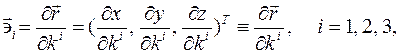
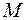 :
: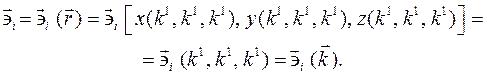
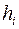 векторов базиса (коэффициенты Ламе) вычисляются по формулам:
векторов базиса (коэффициенты Ламе) вычисляются по формулам: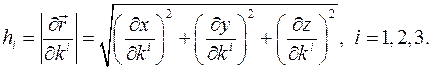
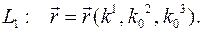
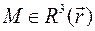 координатные линии пересекаются в этой точке.
координатные линии пересекаются в этой точке.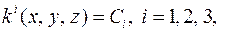
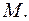
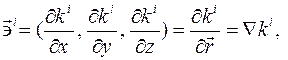
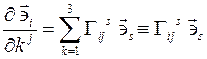 .
.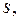 когда один из них находится вверху, а другой – внизу (правило Эйнштейна).
когда один из них находится вверху, а другой – внизу (правило Эйнштейна).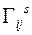 называются символами Кристоффеля второго рода. Они симметричны по нижним индексам:
называются символами Кристоффеля второго рода. Они симметричны по нижним индексам: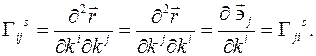
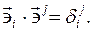
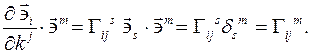
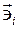 в общем случае не ортогональны и не нормированы, однако имеются системы координат, для которых это не так.
в общем случае не ортогональны и не нормированы, однако имеются системы координат, для которых это не так.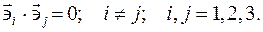
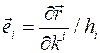
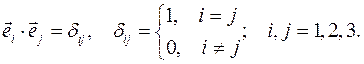
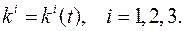
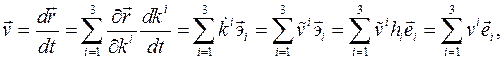
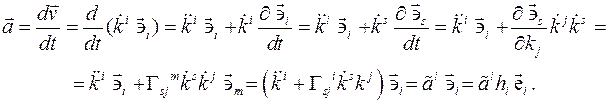
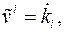
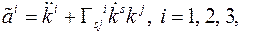
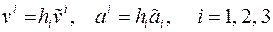 называются физическими компонентами векторов скорости и ускорения.
называются физическими компонентами векторов скорости и ускорения.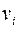 и ускорения
и ускорения 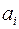 в ортонормированном базисе
в ортонормированном базисе 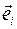 имеют обычную физическую размерность.
имеют обычную физическую размерность.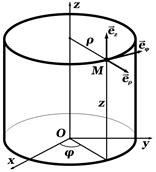 Прямое отображение
Прямое отображение 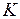 :
: 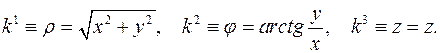
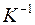 :
:
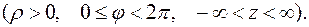
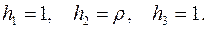
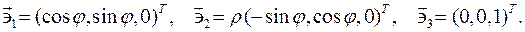
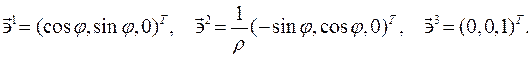
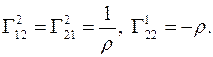
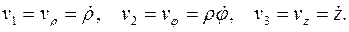
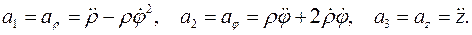
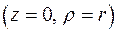 :
: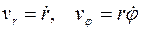
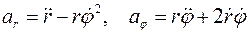 .
.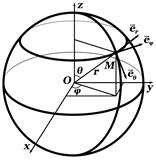 Сферическая ортогональная система координат
Сферическая ортогональная система координат

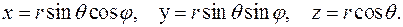
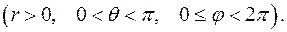
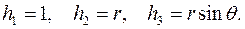
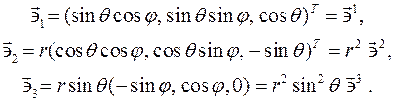
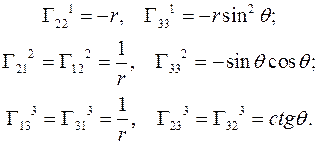
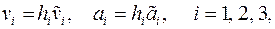
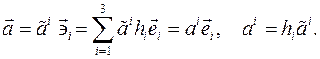
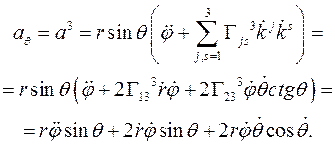

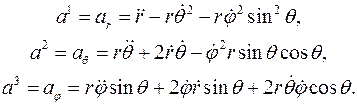
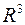 .
.
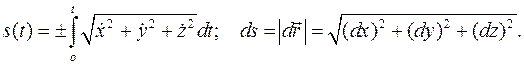
 Далее, примем в качестве параметра вместо времени t дуговую координату s:
Далее, примем в качестве параметра вместо времени t дуговую координату s: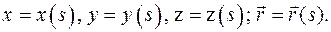
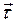 определим следующим образом:
определим следующим образом: 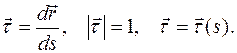
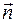 перпендикулярен к вектору
перпендикулярен к вектору 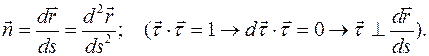
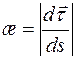 называется кривизной кривой в точке М, а величина
называется кривизной кривой в точке М, а величина 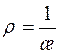 называется радиусом кривизны.
называется радиусом кривизны.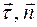 и
и 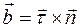 взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.
взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.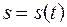
 направлена по касательной
направлена по касательной 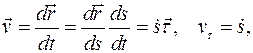

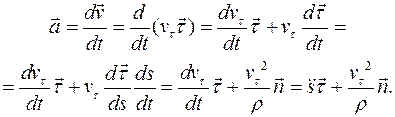
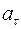 и нормальное
и нормальное 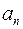 ускорения. Окончательно:
ускорения. Окончательно: