
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение и движение абсолютно твердого тела.
Положение тела в неподвижной системе координат Положение любой точки (элементарной массы) в неподвижном базисе зададим вектором
Определение. Движением абсолютно твердого тела называется гладко зависящее от времени линейное отображение точек подвижной системы координат, связанной с телом, в неподвижную систему координат. Оно осуществляется с помощью гладко зависящего от времени аффинного отображения, вращающаяся часть которого представляется ортогональной матрицей вращения При движении твердого тела относительно неподвижной системы отсчета Ортогональное линейное отображение есть композиция параллельного переноса и поворота. Поэтому для любой точки
Здесь
обратная матрица Задать движение твердого тела – значит задать для всех точек Таким образом, произвольное свободное движение твердого тела задается шестью независимыми параметрами, то есть имеет шесть степеней свободы. Если тело несвободно, то число независимых параметров меньше шести. Это число определяется уравнениями связей. Скорости точек твердого тела. Угловая скорость тела. Скорость любой точки тела определяется в неподвижном базисе:
Матрица Тогда получим
Вектор
так как
где три различных элемента матрицы
Тогда скорость точки тела вычисляется как векторная сумма скорости поступательного движения
Вектор угловой скорости Связь скоростей любых двух точек А и В тела.
Таким образом, проекции скоростей любых двух точек твердого тела Положение и движение любой точки твердого тела при поступательном движении тела. Поступательное движение тела имеет три степени свободы из шести, так как элементы матрицы вращений постоянны, а вектор Введем неподвижную ортогональную систему координат с координатами x, y, z и началом О. Для простоты обозначений абсолютное положение некоторой точки тела
Движение точки тела определяется изменением её положения во времени:
Скорость точки тела есть вектор Компоненты вектора скорости есть производные по времени от компонент вектора движения. Ускорение точки тела есть вектор Компоненты вектора ускорения есть производные по времени от компонент вектора скорости. Компоненты векторов скорости и ускорения (проекции векторов) записаны в декартовом базисе. Траектория точки есть геометрическое место всех последовательных положений точки при ее движении:
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.183 (0.007 с.) |
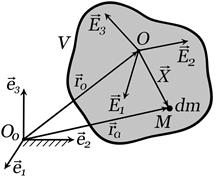 По определению абсолютно твердого тела, при его движении расстояние между любыми двумя точками тела не изменяются.
По определению абсолютно твердого тела, при его движении расстояние между любыми двумя точками тела не изменяются.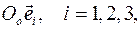 определяется шестью параметрами: три координаты полюса О и три угла между подвижными и неподвижными осями координат. Для индивидуализации положений элементарных масс
определяется шестью параметрами: три координаты полюса О и три угла между подвижными и неподвижными осями координат. Для индивидуализации положений элементарных масс 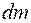 в теле введем вектор
в теле введем вектор 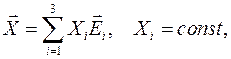 в подвижной системе координат
в подвижной системе координат 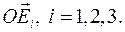
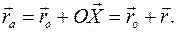
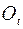 , сохраняющей расстояние между точками тела и ориентацию подвижного базиса.
, сохраняющей расстояние между точками тела и ориентацию подвижного базиса.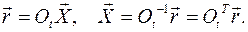 векторов
векторов 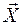 вращается в неподвижной системе координат вместе с телом и постоянен по величине для всех его точек.
вращается в неподвижной системе координат вместе с телом и постоянен по величине для всех его точек.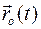 и
и 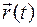 , определяющих соответственно поступательное и вращательное движение как составляющие абсолютного движения твердого тела:
, определяющих соответственно поступательное и вращательное движение как составляющие абсолютного движения твердого тела: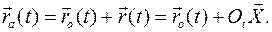
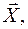 записанных в подвижном базисе. Для таких матриц
записанных в подвижном базисе. Для таких матриц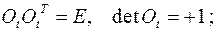
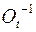 равна транспонированной матрице
равна транспонированной матрице 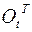 :
: 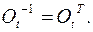
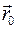 и тремя различными элементами матрицы вращения
и тремя различными элементами матрицы вращения 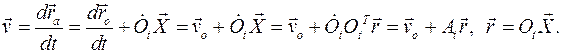
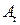 есть антисимметричная матрица, что доказывается так:
есть антисимметричная матрица, что доказывается так: 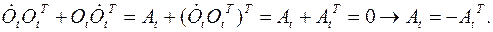
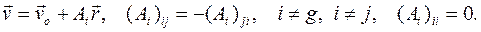
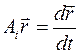 можно представить следующим образом:
можно представить следующим образом: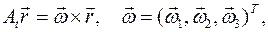
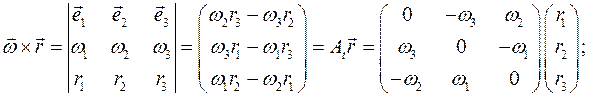
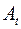 , по определению, образуют вектор угловой скорости твердого тела
, по определению, образуют вектор угловой скорости твердого тела 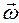 :
: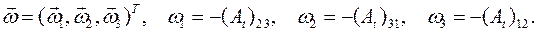
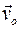 с выбранным началом подвижной системы координат О и скорости вращательного движения
с выбранным началом подвижной системы координат О и скорости вращательного движения 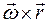 :
: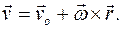
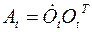 .
.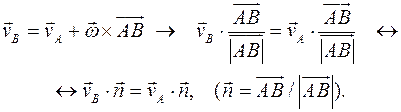
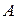 и
и 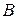 на направление вектора
на направление вектора 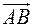 , соединяющего точки, равны.
, соединяющего точки, равны.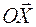 тоже постоянен для всех точек тела и его будем считать нулевым, взяв начало подвижной системы координат в центре масс тела (его положение в теле всегда можно определить). Поэтому все точки тела в любом его положении имеют одинаковые скорости и одинаковые ускорения, а траектории всех точек тела имеют одинаковую форму.
тоже постоянен для всех точек тела и его будем считать нулевым, взяв начало подвижной системы координат в центре масс тела (его положение в теле всегда можно определить). Поэтому все точки тела в любом его положении имеют одинаковые скорости и одинаковые ускорения, а траектории всех точек тела имеют одинаковую форму.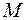 обозначим вектором положения точки
обозначим вектором положения точки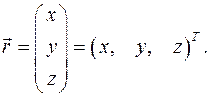
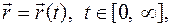
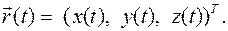
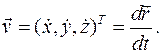
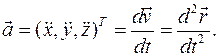
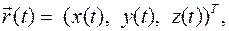
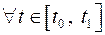 .
.


