Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерционные характеристики абсолютно твердого тела.
Масса тела, а также геометрия пространственного распределения элементарных масс в объеме тела влияют на его способность к ускорению или замедлению поступательного движения или вращения тела вокруг неподвижной оси или подвижной (мгновенной) оси вращения твердого тела. Эти массовые свойства тела называются инерционностью тела. Определения.
Здесь вектор При движении тела центр масс движется в неподвижной системе координат и имеет текущее положение скорость центра масс ускорение центра масс
Выберем в пространстве некоторую прямую линию (ось) в направлении единичного вектора Для некоторого твердого тела с массой
Выберем в теле ортогональную систему координат
Из рисунка видно, что
Поэтому
где выражения в квадратных скобках
есть элементы матрицы линейного отображения
Симметричный линейный оператор Матрица оператора инерции в связанном с телом базисе имеет постоянные элементы, так как все элементарные массы тела имеют фиксированные расстояния от оси
Очевидно, что
Окончательно, осевой момент инерции тела относительно оси
Это есть билинейное отображение вектора Если в декартовых координатах обозначить
Так как выбор осей координат в теле произволен, то, для упрощения вычисления моментов инерции относительно любой оси с направлением Можно доказать, что ось геометрической симметрии однородного тела есть главная ось оператора инерции тела для всех точек оси. Главными осями инерции являются все оси, перпендикулярные к плоскости геометрической симметрии однородного тела. Заметим, что для вычисления осевого момента инерции Формула Гюйгенса - Штейнера. Показывает связь между осевыми моментами инерции относительно двух параллельных осей, одна из которых проходит через центр масс С тела:
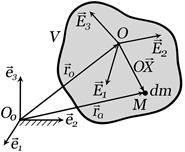
Здесь d - расстояние между параллельными осями. Доказательство.
Так как
По определению центра масс твердого тела еще одно слагаемое в последней формуле равно нулю.
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.212 (0.007 с.) |
 Центр масс С тела есть постоянная в теле точка в системе координат
Центр масс С тела есть постоянная в теле точка в системе координат 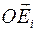 , связанной с телом:
, связанной с телом: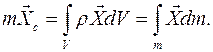
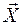 определяет в теле положение элементарной массы тела
определяет в теле положение элементарной массы тела 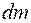 по отношению к началу подвижной системы координат,
по отношению к началу подвижной системы координат, 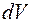 - её элементарный объем. Удельная массовая плотность
- её элементарный объем. Удельная массовая плотность 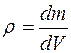 . Массу всего тела обозначим
. Массу всего тела обозначим 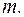
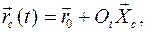
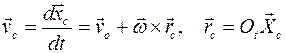 и
и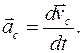
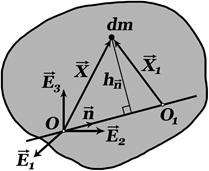 Распределение масс твердого тела по отношению к оси.
Распределение масс твердого тела по отношению к оси. , имеющую одной из своих точек точку
, имеющую одной из своих точек точку  тела.
тела. определим некоторую скалярную величину
определим некоторую скалярную величину 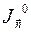 , задающую расположение всех элементарных масс тела
, задающую расположение всех элементарных масс тела 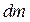 по отношению к оси. Назовем ее моментом инерции телаотносительно оси или осевым моментом инерции тела:
по отношению к оси. Назовем ее моментом инерции телаотносительно оси или осевым моментом инерции тела: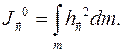
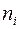 косинусы углов между вектором
косинусы углов между вектором 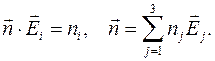 ,
, 
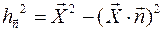 .
.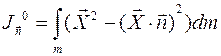
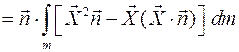
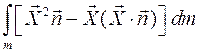 можно представить в виде:
можно представить в виде: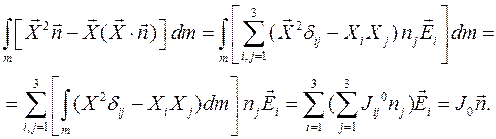
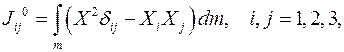
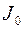 , сопоставляющего вектору
, сопоставляющего вектору 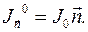
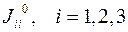 , относительно осей координат, а недиагональные элементы называются центробежные моменты инерции
, относительно осей координат, а недиагональные элементы называются центробежные моменты инерции 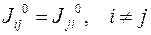 :
: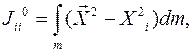
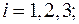
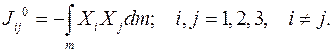
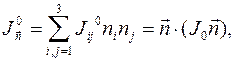
 тела, в число – осевой момент инерции.
тела, в число – осевой момент инерции.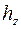 расстояние от элементарной массы dm до оси О z, то
расстояние от элементарной массы dm до оси О z, то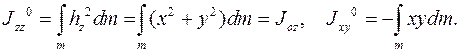
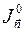 относительно любой оси часто удобней выбирать начало координат не в любой точке
относительно любой оси часто удобней выбирать начало координат не в любой точке 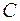 тела.
тела.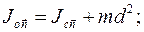
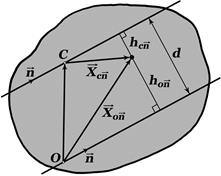 Из рисунка видно, что
Из рисунка видно, что 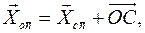
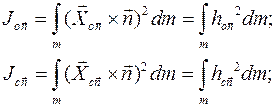 то
то