
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия устойчивости относительного положения равновесия обобщенно – консервативной системы. ⇐ ПредыдущаяСтр 9 из 9
Пусть в равномерно вращающейся системе отсчета движение и взаимодействие тел определяется потенциальными силами, Если функция Гамильтона не зависит явно от времени, то она постоянна на движениях системы:
Положения относительного равновесия
Теорема. Если в положении относительного равновесия Устойчивость проверяется по положительной определенности матрицы
Малые колебания в консервативных и обобщенно – консервативных системах. Малые колебания (движения) есть решения линеаризованных уравнений движения около положений равновесия консервативных систем. В переменных Гамильтона линеаризация есть замена уравнений движения линейными уравнениями с постоянными коэффициентами. Это есть 2 n уравнений первого порядка
В переменных Лагранжа уравнения малых колебанийконсервативной системы около положения равновесия
и есть система n линейных уравнений второго порядка с постоянными коэффициентами, где постоянные элементы элементы матрицы С определяются потенциальной энергией системы
Различные решения уравнений малых колебаний определяются значениями собственных чисел характеристического уравнения матрицы С по отношению к матрице А:
Так как матрица С симметрична, а матрица А симметрична и положительно определена, то все собственные числа действительны, а соответствующие им собственные векторы взаимно ортогональны по метрике матрицы А:
Известно, что пару квадратичных форм линейной заменой переменных
можно привести к главным осям (в них матрица С диагональна, а матрица А единична)
В главных осях уравнения малых колебаний имеют вид:
То есть система этих уравнений распадается на n независимых малых движений, в каждом из которых возможны три случая: 1. 2. 3.
Собственный вектор
Все собственные векторы ортогональны по матрице А:
Собственные векторы
Если среди
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.174 (0.004 с.) |
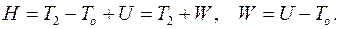
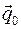 определяются из условия:
определяются из условия: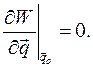
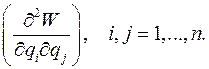
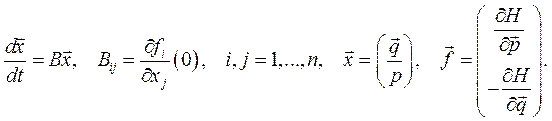
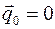 имеют вид:
имеют вид: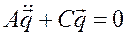
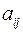 матрицы А определяются через элементы матрицы кинетической энергии в положении равновесия, а
матрицы А определяются через элементы матрицы кинетической энергии в положении равновесия, а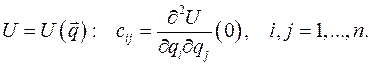
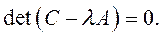
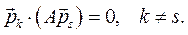
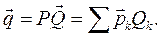
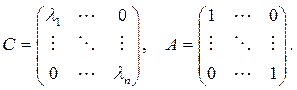
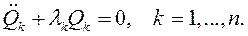
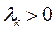 , тогда решение
, тогда решение 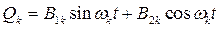 (гармоническое колебание, главное, собственное колебание,
(гармоническое колебание, главное, собственное колебание, 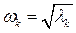 есть главная частота колебаний).
есть главная частота колебаний).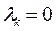 , тогда решение
, тогда решение 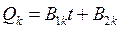 (безразличное равновесие).
(безразличное равновесие).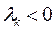 , тогда решение
, тогда решение 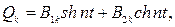 (малое движение, не гармоническое колебание),
(малое движение, не гармоническое колебание), 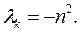
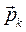 , соответствующий собственному числу
, соответствующий собственному числу 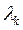 , находится из уравнения:
, находится из уравнения: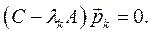
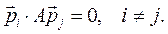
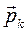 являются столбцами с матрице Р из (19.5), так что запись решений уравнений (19.2) возможна в двух эквивалентных формах:
являются столбцами с матрице Р из (19.5), так что запись решений уравнений (19.2) возможна в двух эквивалентных формах: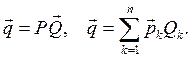
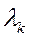 есть кратные собственные числа, то теория остается верна.
есть кратные собственные числа, то теория остается верна.


