
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение угловых скоростей и угловых ускорений в сложном движении твердого тела.
Представим абсолютное движение твердого тела как два движения. Введем неподвижную, абсолютную систему координат Введем подвижную систему координат Наконец, для индивидуализации точек тела, как и раньше, зададим в теле систему координат Исследуем только вращательные части относительного и переносного вращений, заданные матрицами
Абсолютная скорость любой точки тела
Здесь вектор С другой стороны, представляя движение тела как сложное, можем вычислить скорость точки
Таким образом,
Значит, выражение в скобках равно нулю. Здесь В результате получаем теорему о сложении векторов угловых скоростей относительного
Дифференцируя по времени это выражение, докажем теорему о сложении угловых ускорений твердого тела в сложном движении:
Доказательство:
Здесь
Взаимодействие твердых тел. Свойства сил. Центральные силы. Силы с осевой симметрией. Потенциальные силы, потенциальная энергия. Определения. 1. Сила, определяющая движение тела, называется центральной, если ее линия действия в любом положении тела проходит через одну и ту же неподвижную точку О.
3.Элементарной работой силы
4. Сила 5. Сила
Функция U для данной силы называется ее потенциальной энергией. По определению потенциальной энергии, вектор суммы потенциальных сил имеет потенциальную энергию, равную сумме потенциальных энергий всех сил. Элементарная работа силы контактного взаимодействия тела со связями. При точечном контакте тела со связью линия действия силы проходит через точку контакта. Покажем, что работа дискретной силы контакта не зависит от точки приложения силы на ее линии действия. Действительно, пусть одна из точек линии действия силы
так как сила То же самое будет для каждой силы из системы сил твердого тела. Таким образом, элементарная работа дискретной системы сил на элементарных перемещениях твердого тела определяется только положением в теле их линий действия, то есть направлением сил и одной из точек на их линиях действия.
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.9 (0.009 с.) |
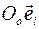 . Тогда абсолютное движение тела определяется движением полюса О и матрицей абсолютного вращения
. Тогда абсолютное движение тела определяется движением полюса О и матрицей абсолютного вращения 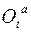 .
.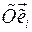 , по отношению которой относительное движение тела определяется относительным движением
, по отношению которой относительное движение тела определяется относительным движением 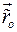 полюса
полюса 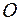 и матрицей относительного вращения
и матрицей относительного вращения 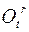 , а переносное движение – движением полюса подвижной системы координат
, а переносное движение – движением полюса подвижной системы координат 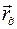 и матрицей ее вращения
и матрицей ее вращения 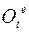 .
.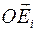 , жестко связанную с телом.
, жестко связанную с телом.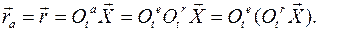
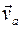 есть для сферического движения
есть для сферического движения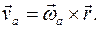
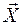 последовательно перезаписывается сначала в подвижном базисе (
последовательно перезаписывается сначала в подвижном базисе (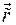 ), а затем в неподвижном (
), а затем в неподвижном (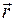 ).
).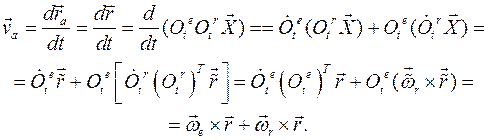
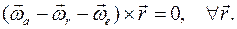
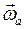 ,
, 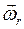 ,
, 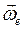 есть угловые скорости абсолютного, относительного и переносного вращений соответственно.
есть угловые скорости абсолютного, относительного и переносного вращений соответственно.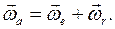
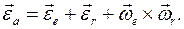
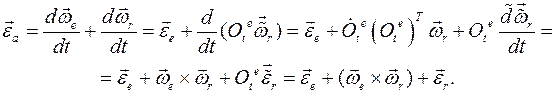
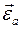 ,
, 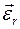 ,
, 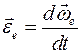 и
и 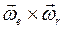 есть абсолютное, относительное и добавочное угловые ускорения.
есть абсолютное, относительное и добавочное угловые ускорения. 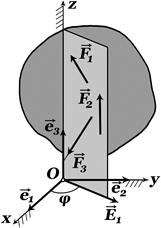 2. Говорят, что с илы имеют осевую симметрию, е сли в любом положении движущегося тела линии действия сил расположены в одной и той же плоскости, связанной с телом, и проходящей через некоторую неподвижную ось координат.
2. Говорят, что с илы имеют осевую симметрию, е сли в любом положении движущегося тела линии действия сил расположены в одной и той же плоскости, связанной с телом, и проходящей через некоторую неподвижную ось координат.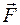 на элементарном перемещении
на элементарном перемещении 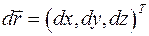 любой точки тела, лежащей на линии действия силы называется скаляр
любой точки тела, лежащей на линии действия силы называется скаляр 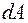 , равный скалярному произведению вектора силы
, равный скалярному произведению вектора силы 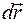 :
: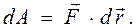
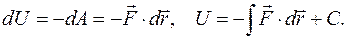
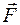 есть точка
есть точка 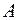 , а другая
, а другая 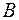 . Определим элементарную работу силы
. Определим элементарную работу силы 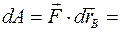
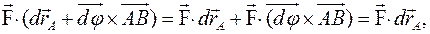
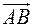 .
.


