
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и Записать интеграл в полярной системе координат.Содержание книги
Поиск на нашем сайте
2. В тройном интеграле
для 3. Найти объем тела, ограниченного поверхностями:
4. Найти массу участка кривой
Варианты индивидуальных заданий 1-ого семестра. Вариант №1 Построить кривую, заданную в полярной системе координат
Вычислить пределы а) б) в) г) Исследовать функцию 3) Найти производные: а) б) в) г) Написать уравнение нормали к кривой 4) Исследовать функцию Вычислить интегралы а) б) в) 6. Найти площадь между кривой Вариант №2 Построить график функции в полярной системе координат
Найти пределы а) б) в) г) Исследовать функцию на непрерывность в точке Вычислить производные а) б) в) г) Написать уравнение касательной к данной кривой в точке 4. Исследовать функцию Вычислить интегралы а) б) в) 6.Вычислить площадь фигуры, ограниченную параболой Вариант №3 Построить график функции в полярной системе координат
Вычислить пределы а) б) в) г) Исследовать функцию на непрерывность Вычислить производные а) б) в) г) Написать уравнение нормали к кривой Исследовать функцию Вычислить интегралы а) б) в) 6) Найти площадь между кривой Вариант №4 Построить в полярной системе график функции
Вычислить пределы а) б) в) г) Исследовать функцию Вычислить производные а) y = x (lnln 2 x - cosln б) в) г) Написать уравнение касательной к кривой 4. Исследовать функцию Вычислить интегралы а) б) в) 6.Вычислить площадь, ограниченную параболой Вариант №5 1. Построить график функции Вычислить пределы а) б) в) г) Исследовать функцию Вычислить производные а) б) в) г) Составить уравнение нормали к кривой, заданной параметрически:
В точке, соответствующей параметру 4. Исследовать функцию Вычислить интегралы а) б) в) 6. Вычислить площадь фигуры, ограниченной:
Вариант № 6 Построить график функции, заданной параметрически
Вычислить пределы а) б) в) г) Исследовать функцию на непрерывность в точке 3. Найти производные: а) б) в) г) Составить уравнение нормали к кривой в точке 4. Исследовать функцию 5. Вычислить интегралы: а) б) в) 6. Вычислить площадь фигуры, ограниченную крив Вариант №7
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |


 , где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.
, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.


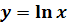 от точки с абсциссой
от точки с абсциссой 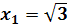 до точки с абсциссой
до точки с абсциссой  , если плотность в каждой точке равна квадрату её абсциссы.
, если плотность в каждой точке равна квадрату её абсциссы.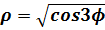
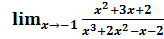
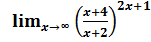

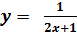 на непрерывность в точке
на непрерывность в точке 



 в точке
в точке 
 и построить ее график
и построить ее график
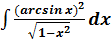

 , осью OX и ординатой
, осью OX и ординатой 
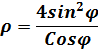

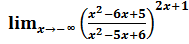






 если
если 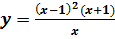
 и построить ее график.
и построить ее график.


 и осью абсцисс.
и осью абсцисс.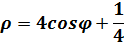



 в точке
в точке 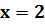



 ;
;  (кривая задана параметрически), в точке соответствующей параметру
(кривая задана параметрически), в точке соответствующей параметру 
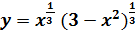 и построить ее график
и построить ее график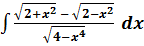
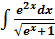
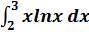
 , осью OX и ординатой
, осью OX и ординатой  .
.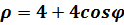



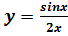 в точке
в точке  на непрерывность
на непрерывность )
)
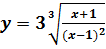
 в точке
в точке 
 и построить ее график
и построить ее график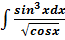

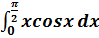
 и прямой
и прямой  .
. в полярной системе координат.
в полярной системе координат.


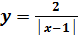 в точке
в точке  на непрерывность
на непрерывность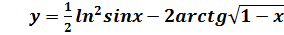
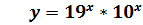

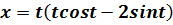
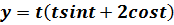
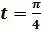
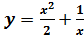 и построить ее график
и построить ее график



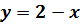


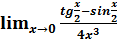
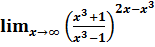


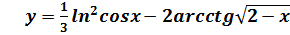
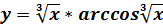
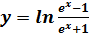
 , если
, если и построить ее график
и построить ее график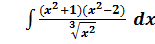


 , прямой
, прямой  и осью oy.
и осью oy.


