
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственные интегралы 1-ого рода.Стр 1 из 15Следующая ⇒
Содержание Введение………………………………………………………………… 1. Несобственные интегралы…………………………………………. 1.1. Несобственные интегралы 1-ого рода………………………… 1.2. Признак сходимости для несобственных интегралов 1-ого рода……………………………………………………….. 1.3. Несобственные интегралы от неограниченных на отрезке [a,b] функций……………………………………………………. 1.4. Признак сходимости для несобственных интегралов 2-ого рода………………………………………………………… 2. Дифференциальное исчисление функций многих переменных…. 2.1 Дифференцирование сложных функций……………………… 2.2 Дифференцирование функций, заданных неявно……………. 2.3 Производная по направлению…………………………………. 2.4 Уравнения касательных плоскостей и нормалей…………....... 2.5 Экстремум функций нескольких переменных………………… 3. Двойные интегралы ……………………………………………….. 3.1.Свойства двойных интегралов…………………………………. 3.2.Вычисления двойных интегралов в декартовой системе координат………………………………………………………… 3.3.Замена переменной в двойном интеграле. Полярная система координат………………………………………………. 3.4.Геометрические и физические приложения двойного интеграла…………………………………………………………. 4. Тройные интегралы ………………………………………………… 4.1.Цилиндрическая и сферическая системы координат…………. 4.2.Геометрические и физические приложения тройных интегралов……………………………………………………….. 5. Криволинейные интегралы 1-ого рода……………………………. 5.1.Задачи на механические приложения криволинейных интегралов………………………………………………………. 6. Поверхностные интегралы 1-ого рода……………………………. 6.1.Задачи на механические приложения поверхностных интегралов……………………………………………………….. Приложения…………………………………………………………….. Введение. Данное пособие содержит разбор и подробное решение типовых задач индивидуальных домашних заданий по математическому анализу, предлагаемых студентам для самостоятельного решения во втором семестре. В данном пособии к каждому из заданий приводятся конспективно изложенные основные сведения из теории, справочные данные, сведения о системах координат на плоскости и в пространстве, а также необходимые формулы, относящиеся к соответствующему разделу. Приведен подробный разбор типовых задач. Представленное пособие позволит студентам экономить время на решение индивидуальных заданий, а также предоставляет широкие возможности для активного самостоятельного изучения практической части курса математического анализа.
В данном пособие подробно рассматриваются типовые задачи индивидуальных домашних заданий по следующим разделам курса «Математического анализа». 1. Несобственные интегралы (вычисление или установление расходимости несобственного интеграла). 2. Дифференцирование функций многих переменных. 3. Двойной интеграл и его приложения. 4. Тройные интегралы и приложения тройных интегралов. 5. Криволинейные интегралы 1-ого рода. 6. Поверхностные интегралы 1-ого рода. В приложении к данному пособию приведены: таблица основных производных и таблица основных методов интегрирования. В пособии приведены варианты индивидуальных домашних заданий и вопросы к экзамену по вышеуказанным разделам курса «Математический анализ».
Несобственные интегралы. Из определения необходимых и достаточных условий существования определенного интеграла следует, что интервал интегрирования [ a; b ] должен быть конечным, а интегрируемая функция f (x) – непрерывна и ограничена на этом интервале. Если хотя бы одно из этих условий не выполняется, то говорят о возможных обобщениях понятия определенный интеграл. Вводится понятие несобственный интеграл. Несобственные интегралы делятся на несобственные интегралы 1-ого рода и несобственные интегралы 2-ого рода.
Производная по направлению. Если функция f (x, y, z) дифференцируема в точке (x, y, z), то для неёимеет смысл производная по направлению любого единичного вектора
l (cos α, cos β, cos γ) и
Т.к. вектор l - единичный, то cos 2 α+ cos 2 β+cos2γ=1 (2.7) Пример: найти производную функции u = x ²-3 yz +5 в точке М(1,2,-1) в направлении, составляющем одинаковые углы со всеми координатными осями. Т.к. α=β=γ, то cos α=cos β= cos γ, тогда в соответствии с формулой (2.7)
2x |M
Пример: найти производную функции z=2y²-xy-2x² в точке P (2;1) в направлении, составляющем с осью O X угол 30°.
Тогда: Двойные интегралы. Индивидуальные домашние задания второго семестра кроме задач на несобственные интегралы и дифференцирование ФМП содержат задачи на интегральное исчисление функций двух и трех независимых переменных. Задания по теме «Двойные интегралы» включают в себя следующие задачи: а) начертить область, на которую распространен двойной интеграл, поменять порядок интегрирования, записать интеграл в полярной системе координат; б) используя представление о декартовой и полярной системах координат на плоскости, решить задачу на приложения двойного интеграла. Задача об объеме цилиндрического тела приводит нас к понятию двойного интеграла. Если функция f(x,y) = f(P) определена и непрерывна в замкнутой ограниченной области D плоскости XOY, а
3.1 Свойства двойного интеграла. а) геометрический смысл двойного интеграла – объем цилиндрического тела
б) если f(x,y) = 1, то численно двойной интеграл равен площади области D
в) константу можно выносить за знак интеграла
г) интеграл от суммы функций равен сумме интегралов
д) если D=
е)
Тройные интегралы Задача о массе пространственного тела переменной плотности f(x,y,z) приводит к понятию тройного интеграла. Под областью “V”,на которую распространен тройной интеграл, понимается ограниченная замкнутая пространственная область, ограниченная снизу и сверху поверхностями
Свойства тройного интеграла аналогичны свойствами двойного интеграла. Таблица производных (u + v - w)′= u ′+ v ′+ w ′ c ′=0 x ′=1 (u·v)′= u′v + v′u (c·u)′= c·u′
(un)′x= n·un-1·u′x (xn)′= n·xn-1 ( (au)′x= au·lna·u′ (ax)′= ax·lna (eu)′= eu·u′ (ex)′= ex (lnu)′= (logau)′= (lgu)′=
( ( (tgu)′= (ctgu)′= - (arccosu)′x= - (arcsinu)′x= (arctgu)′x= (arcctgu)′x=
Варианты заданий на несобственные интегралы и ФМП Вариант № 1 Вариант № 2 Найти производную функции Z= ОХ угол в Вариант № 3 Вариант № 4 Найти производную функции z = Вариант № 5 Вариант № 6 Вариант № 7 Вариант № 8 Вариант № 9
Вариант № 10 Вариант № 11 Вариант № 12 Вариант № 13 Вариант № 14 Варианты заданий на двойные и тройные интегралы Вариант № 1 Вариант № 2 Вариант № 3 Вариант № 4 Вариант № 5 Вариант № 6 Вариант № 7 Вариант № 8 Вариант № 9 Вариант № 10 Вариант № 11 Вариант № 12 Вариант № 13 Вариант № 14 Вариант № 15 Вариант № 16 Вариант № 17 Вариант № 18 Вариант № 19 Вариант № 20 Варианты индивидуальных заданий 1-ого семестра. Вариант №1 Вычислить пределы а) б) в) г) Исследовать функцию 3) Найти производные: а) б) в) г) Написать уравнение нормали к кривой 4) Исследовать функцию Вычислить интегралы а) б) в) 6. Найти площадь между кривой Вариант №2 Найти пределы а) б) в) г) Исследовать функцию на непрерывность в точке Вычислить производные а) б) в) г) Написать уравнение касательной к данной кривой в точке 4. Исследовать функцию Вычислить интегралы а) б) в) 6.Вычислить площадь фигуры, ограниченную параболой Вариант №3 Вычислить пределы а) б) в) г) Исследовать функцию на непрерывность Вычислить производные а) б) в) г) Написать уравнение нормали к кривой Исследовать функцию Вычислить интегралы а) б) в) 6) Найти площадь между кривой Вариант №4 Вычислить пределы а) б) в) г) Исследовать функцию Вычислить производные а) y = x (lnln 2 x - cosln б) в) г) Написать уравнение касательной к кривой 4. Исследовать функцию Вычислить интегралы а) б) в) 6.Вычислить площадь, ограниченную параболой Вариант №5 1. Построить график функции Вычислить пределы а) б) в) г) Исследовать функцию Вычислить производные а) б) в) г) Составить уравнение нормали к кривой, заданной параметрически:
В точке, соответствующей параметру 4. Исследовать функцию Вычислить интегралы а) б) в) 6. Вычислить площадь фигуры, ограниченной:
Вариант № 6 Вычислить пределы а) б) в) г) Исследовать функцию на непрерывность в точке 3. Найти производные: а) б) в) г) Составить уравнение нормали к кривой в точке 4. Исследовать функцию 5. Вычислить интегралы: а) б) в) 6. Вычислить площадь фигуры, ограниченную крив Вариант №7 Вычислить пределы а) б) в) г) Исследовать функцию Вычислить производные а) б) в) г) Написать уравнение нормали в точке 4.Исследовать функцию 5. Вычислить интегралы: а) б) в) 6. Вычислить площадь фигуры ограниченной кривой Вариант №8 1. Построить график функции в полярной системе координат Найти пределы а) б) в) г) Исследовать функцию на непрерывность в точке Найти производные а) б) в) г) Написать уравнение касательной к кривой 4. Исследовать функцию Вычислить интегралы а) б) в) 6. Вычислить площадь фигуры, ограниченную параболой
| Поделиться:
| |

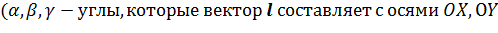 , OZ)
, OZ)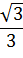
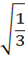 cos2 α=cos2 β= cos2 γ=1/3, т.е. cos α=cos β= cos γ= =
cos2 α=cos2 β= cos2 γ=1/3, т.е. cos α=cos β= cos γ= =

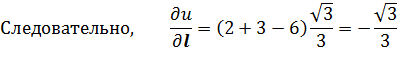


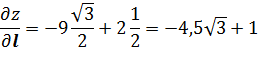
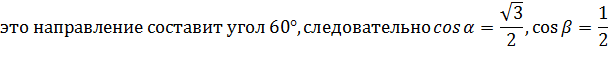
 - площади элементарных подобластей, полученных разбиением области D, диаметры которых d
- площади элементарных подобластей, полученных разбиением области D, диаметры которых d  , то предел интегральных сумм (если он существует) называется двойным интегралом от функции f (x,y) по области D:
, то предел интегральных сумм (если он существует) называется двойным интегралом от функции f (x,y) по области D: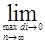

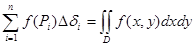
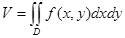
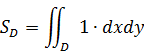
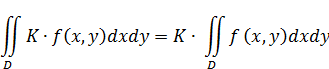
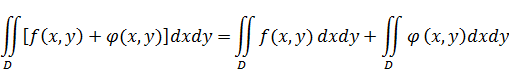
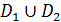 , где
, где 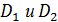 - не пересекаются, то
- не пересекаются, то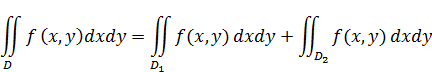
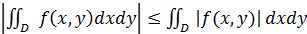
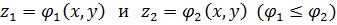 , а с боков – цилиндрической поверхностью с образующими, параллельными оси OZ. Переменные x и y изменяются в плоской области
, а с боков – цилиндрической поверхностью с образующими, параллельными оси OZ. Переменные x и y изменяются в плоской области 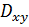 , которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.
, которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.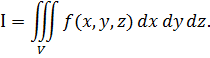
 ′=
′= 
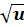 )′=
)′= 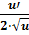 (
(  )′=
)′= 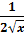
 ′= -
′= - 
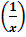 ′= -
′= - 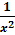
 (lnx)′=
(lnx)′= 
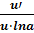 (logax)′=
(logax)′= 
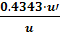 (lgx)′=
(lgx)′= 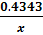
 )′x=
)′x= 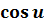 ·u′ (
·u′ (  )′=
)′= 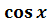
 ′x=-
′x=-  )′= -
)′= -  (tgx)′=
(tgx)′= 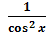
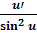 (ctgx)′= -
(ctgx)′= - 
 (arccos x)′= -
(arccos x)′= - 
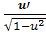 (arcsin x)′=
(arcsin x)′= 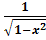
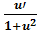 (arctgx)′=
(arctgx)′= 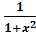
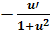 (arcctgx)′= -
(arcctgx)′= - 
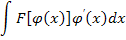
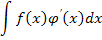
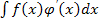 =f(x)φ(x)-
=f(x)φ(x)- 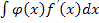 Метод интегрирования по частям применяется, например, к интегралам вида
Метод интегрирования по частям применяется, например, к интегралам вида 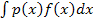 , где
p(x) – многочлен,
eax;cos ax;sin ax;lnx;arctg x;arcsin x и т.п.,а
также к интегралам от произведений показательной функции на косинус или синус.
, где
p(x) – многочлен,
eax;cos ax;sin ax;lnx;arctg x;arcsin x и т.п.,а
также к интегралам от произведений показательной функции на косинус или синус.
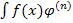 (x)dx
(x)dx
 (x)φ(x) с помощью формулы кратного
интегрирования по частям:
(x)φ(x) с помощью формулы кратного
интегрирования по частям: 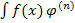 (x)dx=
=f(x)
(x)dx=
=f(x)  -f′(x)
-f′(x)  +
+f′′(x)
+
+f′′(x)  (x)-…
…+(-1)n-1f(n-1)(x)φ(x)+
+(-1)n
(x)-…
…+(-1)n-1f(n-1)(x)φ(x)+
+(-1)n 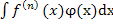
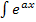 pn(x)dx
pn(x)dx
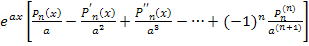 +C
+C
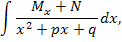 P3-4q<0
P3-4q<0
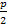 =t
=t
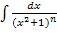
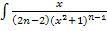 +
+  In-1
In-1
 dx, где
dx, где  -правильная
рациональная дробь,
Q(x)=(x-x1)′(x-x2
-правильная
рациональная дробь,
Q(x)=(x-x1)′(x-x2  ...
…(
...
…(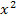 +px+q
+px+q  …
…
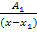 +
+ 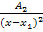 +…+
+…+  +
+
+
+  +
+  +…
+…
 +…+
+…+ 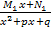 +
+
 +…+
+…+ 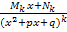 +…
+…
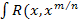 ,…,
,…,  )dx,
где R-рациональная функция своих аргументов
)dx,
где R-рациональная функция своих аргументов
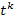 , где k – общий знаменатель дробей
, где k – общий знаменатель дробей
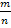 ,…,
,…, 
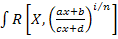 dx
dx
 =
= 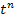
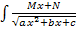 dx
dx
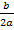 =t интеграл приводится к
сумме двух интегралов
=t интеграл приводится к
сумме двух интегралов
 +
+N1
+
+N1  Первый интеграл сводится к интегралу от степенной функции, а второй интеграл – табличный.
Первый интеграл сводится к интегралу от степенной функции, а второй интеграл – табличный.
 )dx,
где R –рациональная функция
от x и
)dx,
где R –рациональная функция
от x и 
 (a>0),
(a>0),
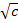 (c>0)
(c>0)
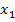 ) (4ac-
) (4ac- 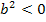 ),
где
),
где  Для вычисления указанного интеграла применяются также тригонометрические подстановки:
x+
Для вычисления указанного интеграла применяются также тригонометрические подстановки:
x+ 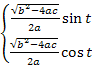 (a<0, 4ac-b2<0)
x+
(a<0, 4ac-b2<0)
x+ 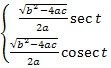 (a>0, 4ac-b2<0)
x+
(a>0, 4ac-b2<0)
x+ 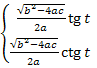 (a>0, 4ac-b2>0)
(a>0, 4ac-b2>0)
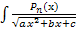 dx
где
dx
где 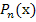 - многочлен степени n
- многочлен степени n
 =Qn-1(x)
=Qn-1(x) 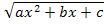 +
+k
+
+k 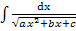 ,
где Qn-1(x)- многочлен степени n-1
Дифференцируя обе части этого равенства и умножая на
,
где Qn-1(x)- многочлен степени n-1
Дифференцируя обе части этого равенства и умножая на 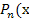 )= Qn-1(x)(
)= Qn-1(x)(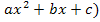 +
+
+
+ 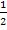 Qn-1(x)(2ax+b)+k
Которое дает систему n+1 линейных уравненений для определения коэффициентов многочлена Qn-1(x) и множителя k.
Интеграл же
Qn-1(x)(2ax+b)+k
Которое дает систему n+1 линейных уравненений для определения коэффициентов многочлена Qn-1(x) и множителя k.
Интеграл же
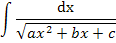 берется методом, указанным в п.10 (M=0;N=1)
берется методом, указанным в п.10 (M=0;N=1)

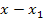 =
= 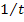 к интегралу рассмотренному выше.
к интегралу рассмотренному выше.
 (a+b
(a+b 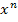 )pdx,
Где m,n,p-рациональные числа (интеграл от биноминального дифференциала)
)pdx,
Где m,n,p-рациональные числа (интеграл от биноминального дифференциала)
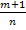 – целое число
3) если
– целое число
3) если  - целое число, то применяется
подстановка a+b
- целое число, то применяется
подстановка a+b 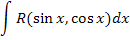
 =t
Если R(-
=t
Если R(- 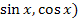 = - R(
= - R(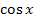 =t.
Если
R(
=t.
Если
R(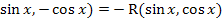 ,то
подстановка
,то
подстановка  =t.
Если
R(
=t.
Если
R(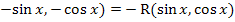 ,то
подстановка
,то
подстановка 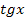 =t.
=t.
 =t.
При этом
sh x=
=t.
При этом
sh x=  ;ch x=
;ch x=  ;dx=
;dx= 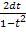
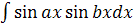
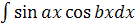
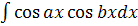
 =
= 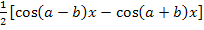
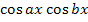 =
=
=
= 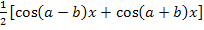
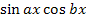 =
=
=
= 
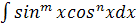 ,
где m и n – целые числа
,
где m и n – целые числа
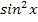 =
=  ;
; 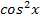 =
= 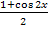
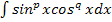 ,
(0<x<
,
(0<x< 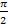 )
p и q- рациональные числа
)
p и q- рациональные числа
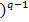 dt
dt
 )dx
)dx
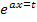 преобразуется в интеграл от рациональной функции.
преобразуется в интеграл от рациональной функции.
 - xy -2
- xy -2  в точке P(1;2) в направлении, составляющем с осью
в точке P(1;2) в направлении, составляющем с осью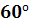
 -2
-2  + x
+ x 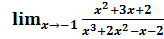
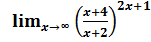

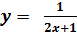 на непрерывность в точке
на непрерывность в точке 



 в точке
в точке 
 и построить ее график
и построить ее график
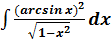

 , осью OX и ординатой
, осью OX и ординатой 

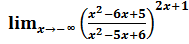






 если
если 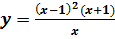
 и построить ее график.
и построить ее график.


 и осью абсцисс.
и осью абсцисс.


 в точке
в точке 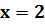



 ;
;  (кривая задана параметрически), в точке соответствующей параметру
(кривая задана параметрически), в точке соответствующей параметру 
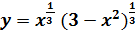 и построить ее график
и построить ее график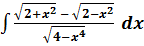
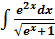
 , осью OX и ординатой
, осью OX и ординатой  .
.


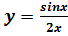 в точке
в точке  на непрерывность
на непрерывность )
)
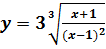
 в точке
в точке 
 и построить ее график
и построить ее график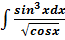

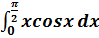
 и прямой
и прямой  .
. в полярной системе координат.
в полярной системе координат.


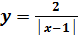 в точке
в точке  на непрерывность
на непрерывность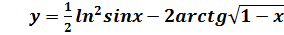
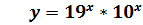

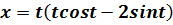
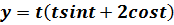
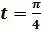
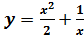 и построить ее график
и построить ее график



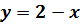
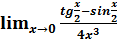
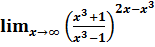


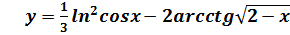
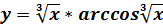
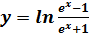
 , если
, если и построить ее график
и построить ее график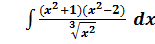


 , прямой
, прямой  и осью oy.
и осью oy.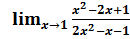
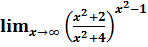

 в точке
в точке  на непрерывность.
на непрерывность.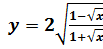
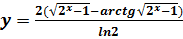

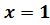 к кривой
к кривой 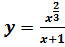
 и построить ее график.
и построить ее график.


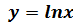 осью ox и прямой
осью ox и прямой  .
.
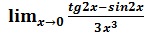
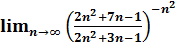

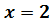 , если
, если 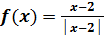
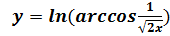
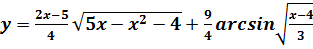

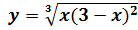 в точке
в точке 
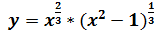 и построить ее график.
и построить ее график.





