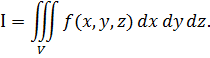Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменной в двойном интеграле. Полярная система координат.
Замена переменной в интеграле x= X (u, v), y = Y (u,v), (u,v) При выполнении условий, что отображение (3.4) взаимно однозначно, а функции в соотношении (3.4) непрерывно-дифференцируемы, то якобиан отображения – определитель, составленный из первых частных производных:
тогда имеет место формула:
Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами:
В полярных координатах полюс совпадает с началом координат, полярная ось – с положительным направлением оси Ох, угол φ (положительный) отсчитывается от полярной оси против часовой стрелки. Якобиан преобразования равен:
Если D =
Пример: построить область интегрирования и перейти к полярной системе координат
Порядок интегрирования соответствует формуле (3.1):
Возводя в квадрат правую и левую части и дополняя до полного квадрата разности, получили уравнение окружности
т.к. в верхнем пределе перед корнем нет знака, то приписывается знак плюс. Т.е. верхняя граница области D – верхняя часть окружности Нижняя граница:
Переносим
Получили уравнение окружности
Рис. 3.8 Область интегрирования D - область между двумя выше указанными окружностями. Точка пересечения A (
Окружность Окружность
Студентам рекомендуется запомнить следующее правило. Если центр окружности сдвинут по оси Ох вправо, ровно на радиус окружности R, то в полярной системе координат уравнение такой окружности Окончательно в полярной системе координат двойной интеграл примет вид: I=
Пример: начертить область на которую, распространяется двойной интеграл, изменить порядок интегрирования, записать интеграл в полярной системе координат.
Рис. 3.9 Уравнение нижней окружности:
Уравнение верхней окружности: x ²+ y ²=2. В декартовой системе координат заданный интеграл примет вид:
Используя вышеприведенное правило в полярной системе координат при π≤φ≤7π/6 двойной интеграл примет вид:
Геометрические и физические приложения двойного интеграла. Пусть G – материальная пластинка (квадрируемая фигура) на плоскости с плотностью 1. Площадь пластины 2. Масса пластины m= 3. Статические моменты пластинки относительно осей Ox и Oy
4. Координаты центра тяжести пластинки 5. Моменты инерции пластинки относительно осей Ox и Oy
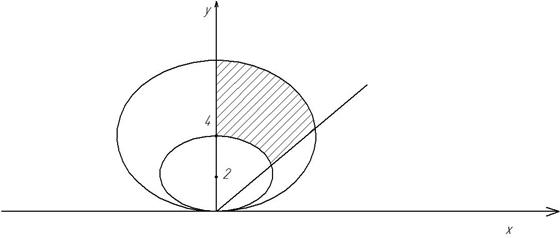
6. Момент инерции пластинки относительно начала координат Пример: вычислить площадь пластины ограниченной линиями: y=x; y=0; y ²-4 y + x ²=0; y ²-8 y + x ²=0 Запишем уравнения линий, ограничивающих область интегрирования: y ² - 4 y + x ² =0 y
Окружность с центром, Окружность с центром, сдвинутым по у на 4 единицы сдвинутым по у на 2 единицы
Рис. 3.10 Уравнения окружностей, в соответствии с вышеизложенным правило примут вид : ρ=4∙ sinφ и ρ=8∙ sinφ.
Пример: вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением Проведем замену переменных: x=ρcosφ, y= ρsinφ. Тогда заданная кривая в полярной системе координат примет вид:
Рис.3.11 Тогда С учетом симметрии фигуры (рис. 3.11), вычислим площадь четвертой части и результат умножим на четыре. Вычислим площадь по формуле
Площадь всей фигуры, ограниченной данной линией, S=2 Пример: найти массу пластинка G, если она задана ограничивающими её кривыми (рис. 3.12): x = 0, y = 0,
Рис. 3.12
Пластинка расположена в прямоугольной системе координат таким образом, что центры окружностей совпадают с началом координат.
Масса плоской пластины вычисляется по формуле:
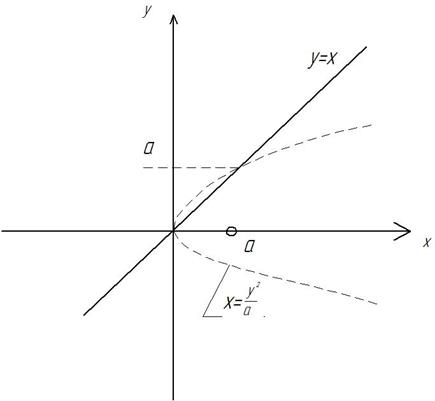
Пример: найти статические моменты относительно координатных осей Ох и Oy однородной фигуры, ограниченной кривыми y²=ax, y=x (рис. 3.13) Т.к. фигура однородная, примем поверхностную плотность μ=const=1.
Рис.3.13
Статический момент относительно оси Ох
Статический момент относительно оси Оу
Тройные интегралы Задача о массе пространственного тела переменной плотности f(x,y,z) приводит к понятию тройного интеграла. Под областью “V”,на которую распространен тройной интеграл, понимается ограниченная замкнутая пространственная область, ограниченная снизу и сверху поверхностями
Свойства тройного интеграла аналогичны свойствами двойного интеграла.
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.132.214 (0.027 с.) |
 состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями
состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями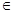 D. (3.4)
D. (3.4)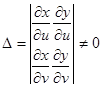
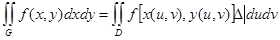 (3. 5)
(3. 5)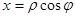 ,
,  ,
, 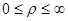 , (3.6)
, (3.6)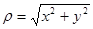 ;
; 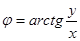
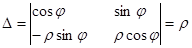
 , то
, то (3.7)
(3.7)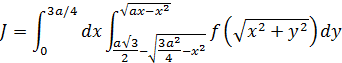
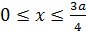 ; верхняя граница
; верхняя граница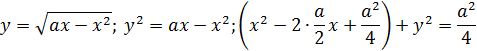
 с центром (
с центром (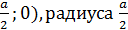

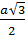 в левую часть и возводим правую и левую часть в квадрат
в левую часть и возводим правую и левую часть в квадрат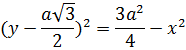
 с центром
с центром 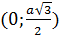 радиуса
радиуса 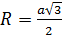

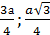 ). Вся область D находится в первом квадранте, следовательно
). Вся область D находится в первом квадранте, следовательно  , но область ограничена двумя разными окружностями. Проведем луч из начала координат в точку А. Тогда область разделится на две части.
, но область ограничена двумя разными окружностями. Проведем луч из начала координат в точку А. Тогда область разделится на две части.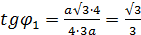 , следовательно,
, следовательно, 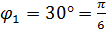 . Тогда в полярной системе координат область интегрирования и сам двойной интеграл разбиваются на две части: 0≤ φ≤π/6 и π/6≤φ≤π/2.
. Тогда в полярной системе координат область интегрирования и сам двойной интеграл разбиваются на две части: 0≤ φ≤π/6 и π/6≤φ≤π/2.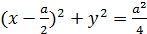 в полярной системе примет вид
в полярной системе примет вид 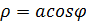
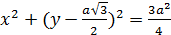 в полярной системе примет вид
в полярной системе примет вид 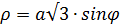
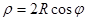 , если влево на радиус, то
, если влево на радиус, то  . Если центр окружности сдвинут на радиус по оси Оy вверх – уравнение окружности в полярной системе
. Если центр окружности сдвинут на радиус по оси Оy вверх – уравнение окружности в полярной системе 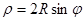 , если же центр окружности сдвинут ровно на радиус вниз, то
, если же центр окружности сдвинут ровно на радиус вниз, то 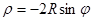 . Это правило легко выводится из соотношений (3.6).
. Это правило легко выводится из соотношений (3.6).


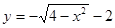
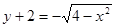

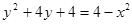
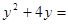
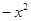
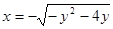
 порядок интегрирования изменен, где
порядок интегрирования изменен, где  (нижний предел интегрирования во внутреннем интеграле).
(нижний предел интегрирования во внутреннем интеграле).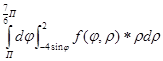 - двойной интеграл в полярной системе координат.
- двойной интеграл в полярной системе координат.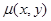
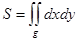
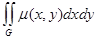


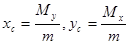
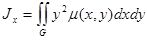 ,
, 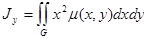



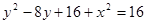

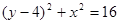
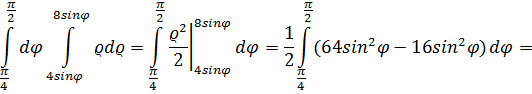
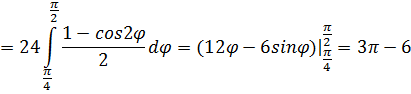
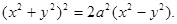

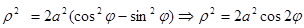
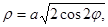 где
где 

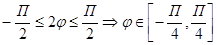 С учетом того, что cos2
С учетом того, что cos2 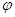 имеет период Т=π, и ρ≥0 параметр
имеет период Т=π, и ρ≥0 параметр 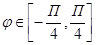
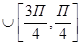
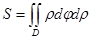
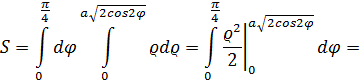
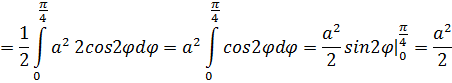
 .
.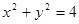 ,
, 
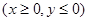
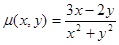 - поверхностная плотность.
- поверхностная плотность.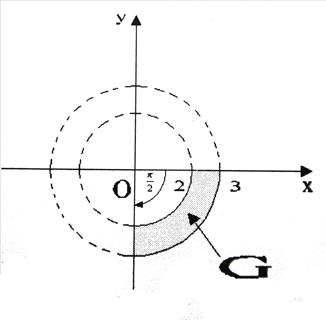
 . Перейдем в двойном интеграле к полярным координатам
. Перейдем в двойном интеграле к полярным координатам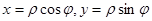 при этом область G преобразуется в прямоугольную область в полярной системе координат: 2≤ρ≤3, -π/2 ≤φ≤0, поверхностная плотность:
при этом область G преобразуется в прямоугольную область в полярной системе координат: 2≤ρ≤3, -π/2 ≤φ≤0, поверхностная плотность: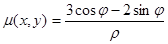
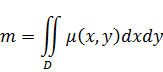
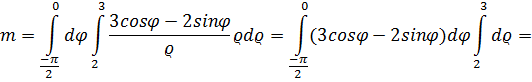
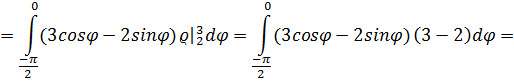

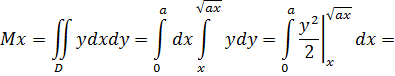
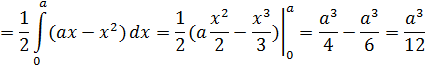


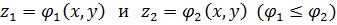 , а с боков – цилиндрической поверхностью с образующими, параллельными оси OZ. Переменные x и y изменяются в плоской области
, а с боков – цилиндрической поверхностью с образующими, параллельными оси OZ. Переменные x и y изменяются в плоской области 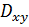 , которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.
, которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.