Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремум функции нескольких переменных.Содержание книги
Поиск на нашем сайте
Функция f (x 1, x 2,…, xn) имеет максимум (минимум) в точке Р, если для всех отличных от Р точек Р1 в достаточно малой окрестности точки Р выполняется неравенство f (p)< f (p 1). Максимум или минимум функции называется локальным экстремумом. Точки, в которых дифференцируемая функция f (x 1, x 2,…, xn) может достигать экстремума, называются стационарными точками.
Из решения системы уравнений (2.12) находят координаты стационарных точек. Достаточные условия экстремума. Пусть функция u = f (P) дважды непрерывно дифференцируема в окрестности её стационарной точки Р0. Тогда если второй дифференциал d 2 u (P 0) в окрестности точки Р0 имеет постоянный знак, то функция имеет максимум в точке Р0, если d 2 u (P 0)<0 и минимум, если d 2 u (P 0)>0. Для функции двух переменных z = f (x, y) достаточные условия формулируются следующим образом. Пусть P 0 (x 0; y 0)- стационарная точка функции z = f (x, y) и
Тогда: а) если D >0, то в точке P 0 (x 0; y 0) есть экстремум, причём максимум, если A <0 и минимум, если A >0; б) если D <0, экстремума в точке P 0 (x 0; y 0) нет; в) если D =0 – требуются дополнительные исследования. Пример: исследовать функцию на экстремум z =2 x 3 +2 y 3 -36 xy +430. Находим первые частные производные
Найдём стационарные точки, решив систему:
Из первого уравнения y =, подставив его во второе уравнение, получим x 4 -216 x =0, которое запишем так x (x 3 -216)=0. Разлагая на множители выражение в скобках получим: x (x -6)(x 2 +6 x +36)=0. Данное уравнение имеет два действительных корня x 1 =0, x 2 =6. Получили две стационарные точки P 1 (0;0) и P 2 (6;6).
A= =12x; C= =12y; B= = -36
Точка Р1(0;0): A =0; C =0; D = AC - B 2 <0, т.е. в точке P 1 (0;0) экстремума нет. Точка P 2 (6;6): A =72; C =72: D =72·72-362>0 - в точке Р2(6;6)- экстремум есть, а т.к. A =72>0, то имеет место минимум zmin =-2. Пример: найти стационарные точки и исследовать их характер у функции z=x 3 +y 3 -3xy
, т.е. x = y 2, подставим это равенство в первое уравнение, получим 3 y 4 -3 y =0; 3 y (y 3 -1)=3 y (y -1)(y 2 + y +1)=0.
Возможны два решения y =0, тогда и x =0, т.е. первая стационарная точка Р1(0;0). Или y=1, тогда x=1, вторая стационарная точка Р2(1;1).
A=
т.е. в точке Р2(1;1)- минимум. Zmin (1;1)=-1 Двойные интегралы. Индивидуальные домашние задания второго семестра кроме задач на несобственные интегралы и дифференцирование ФМП содержат задачи на интегральное исчисление функций двух и трех независимых переменных. Задания по теме «Двойные интегралы» включают в себя следующие задачи: а) начертить область, на которую распространен двойной интеграл, поменять порядок интегрирования, записать интеграл в полярной системе координат; б) используя представление о декартовой и полярной системах координат на плоскости, решить задачу на приложения двойного интеграла. Задача об объеме цилиндрического тела приводит нас к понятию двойного интеграла. Если функция f(x,y) = f(P) определена и непрерывна в замкнутой ограниченной области D плоскости XOY, а
3.1 Свойства двойного интеграла. а) геометрический смысл двойного интеграла – объем цилиндрического тела
б) если f(x,y) = 1, то численно двойной интеграл равен площади области D
в) константу можно выносить за знак интеграла
г) интеграл от суммы функций равен сумме интегралов
д) если D=
е)
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.32.98 (0.006 с.) |

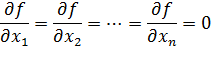 Необходимые условия экстремума. Если дифференцируемая функция u = f (P) достигает экстремума в точке Р0,то в этой точке все её первые частные производные обращаются в ноль, т.е. (2.12)
Необходимые условия экстремума. Если дифференцируемая функция u = f (P) достигает экстремума в точке Р0,то в этой точке все её первые частные производные обращаются в ноль, т.е. (2.12)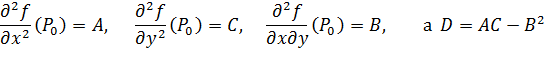
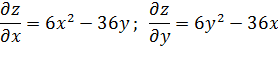
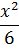
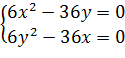
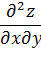
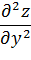
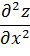 Проверим достаточные условия для каждой из точек:
Проверим достаточные условия для каждой из точек: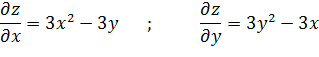
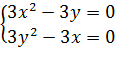 Составляем систему для нахождения стационарных точек:
Составляем систему для нахождения стационарных точек: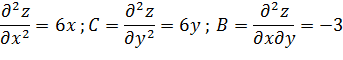 Проверим достаточные условия для каждой из точек;
Проверим достаточные условия для каждой из точек;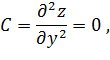 Р1(0;0): A= =0; т.е. D=0·0-(-3)2 <0-экстремума нет.
Р1(0;0): A= =0; т.е. D=0·0-(-3)2 <0-экстремума нет.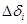 - площади элементарных подобластей, полученных разбиением области D, диаметры которых d
- площади элементарных подобластей, полученных разбиением области D, диаметры которых d 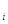 , то предел интегральных сумм (если он существует) называется двойным интегралом от функции f (x,y) по области D:
, то предел интегральных сумм (если он существует) называется двойным интегралом от функции f (x,y) по области D: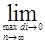

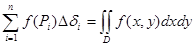
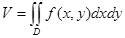
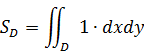
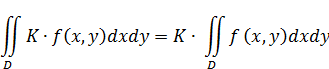
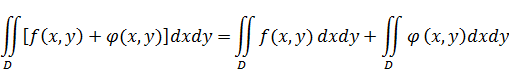
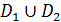 , где
, где 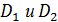 - не пересекаются, то
- не пересекаются, то