Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Финансовые ресурсы и капиталСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Всякий собственник, имеющий квартиру или гараж, которые он не использует, может сдать их в наем, получая за это определенную плату. Точно также человек, имеющий деньги, которые он не использует, может их дать взаймы другому лицу (или, используя более общий термин, -инвестировать) за определенное вознаграждение. Доход от инвестированного капитала или, в более узком смысле, вознаграждение за использование денег, называется процентными деньгами или кратко процентами. Сумма денег, данных взаймы, называется основной или капиталом. Обычно заем дается на определенное время - период. Сумма процентных и основных денег, полагающаяся в конце периода, называется итогом. В общем случае отношение процента за период к основной сумме (капиталу) называется нормой процента. Эта норма чаще всего выражается в форме процентов, при расчетах используются эквивалентные десятичные (реже - натуральные) дроби. При заключении конкретных сделок для обозначения нормы процентов обычно используется другое название - процентная ставка. Основные положения 1. Денежные ресурсы, участвующие в финансовой операции, имеют временную ценность: одна и та же сумма денег неравноценна в разные периоды. Учет временного фактора в финансовых операциях осуществляется путем начисления процентов или дисконтирования. 2. Для сопоставления в пространственно-временном аспекте результатов финансовой операции используют показатель, называемый ставкой и определяемый отношением процентных денег, уплаченных (полученных) за единицу времени (обычно за год), к некоторому базовому капиталу. Это отношение выражается в десятичных дробях или в процентах. 3. Процентная ставка определяется отношением процентных денег, уплаченных (полученных) за единицу времени (обычно за год), к величине исходного капитала. 4. Учетная ставка определяется отношением процентных денег, уплаченных (полученных) за единицу времени (обычно за год), к ожидаемой к получению (возвращаемой) сумме денежных средств. 5. Эффективность любой финансовой операции может быть охарактеризована ставкой. 6. Удобной и наглядной характеристикой (особенно при оценке вклада) является индекс роста суммы за данный период, показывающий, во сколько раз выросла величина капитала по отношению к величине капитала в конце предыдущего период. 7. Процесс, в котором заданы исходная сумма и ставка, в финансовых вычислениях называется процессом наращения, искомая величина называется наращенной суммой, а ставка – ставкой наращения. 8. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования, искомая величина называется приведенной суммой, а ставка – ставкой дисконтирования. 9. В качестве ставки наращения или дисконтирования может выступать как процентная, так и учетная ставка. 10. Число, равное сумме начального числа и начисленных на него процентов, называется наращенным числом. Проценты по отношению к наращенному числу называются «на 100», а проценты по отношению к начальному числу называются процентами «со 100». Проценты «на 100» находят в задачах следующего типа: даны ставка процента и сумма двух слагаемых, одно из которых представляет собой проценты «со 100» другого; требуется найти одно из слагаемых. 11. Число, равное разности между начальным числом и начисленными на него процентами, называется уменьшенным числом. Проценты по отношению к уменьшенному числу называются процентами «во 100». Проценты «во 100» находят в задачах следующего типа: даны ставка процента и разность двух слагаемых, одно из которых (вычитаемое) представляет собой проценты «со 100» другого; требуется найти одно из слагаемых.
2.1 УЧЕТНЫЕ СТАВКИ Пример. Предприниматель получил на полтора года кредит в размере 40 тыс. руб. с условием возврата 50 тыс. руб. Определите процентную ставку, учетную ставку и дисконт-фактор за полтора года. Чему равен индекс роста суммы кредита? Решение. Полагая в формуле (1) (см. приложение 1) t = 1,5 года, PV = 40 тыс. руб., получим величину процентной ставки за полтора года:
Аналогичным образом учетную ставку и дисконт-фактор находим соответственно по формулам (2), (4):
Заметим, что величины
Индекс роста
ПРИМЕР Иванов взял в сберегательном банке ссуду 10000 руб. Если банк начисляет 250 руб. процентных денег за использование этой суммы в течение 6 месяцев, какой будет норма процента за этот период? РЕШЕНИЕ Обозначим норму процента за шести месячный период через i. Тогда i = 250/10000 = 0.025 = 2.5%. 2.2 ПРОСТОЙ ПРОЦЕНТ Пусть P будет основной суммой. r - нормой процента за 1год и t - продолжительность периода времени в годах. Если процент вычисляется по формуле I = Prt (1) и если процент выплачивается в конце периода времени, тогда выплачиваемые процентные деньги называются простым процентом. В этом случае норма процента за рассматриваемый период времени равна rt. Для простого процента норма, как правило, дается для периода продолжительностью 1 год. Если S обозначает итоговую сумму, тогда S = P + I (2) Равенства (1) и (2) называются основными уравнениями простого процента. Любая задача для простых процентов может быть решена при помощи этих двух равенств. Следует заметить, что они содержат пять различных переменных, а именно S, P, I, r и t. Если любые три заданы (исключая случай задания трех первых одновременно), остальные две могут быть найдены с помощью (1) и (2). Для удобства можно добавить еще одно равенство. Если исключить из (1) и (2) переменную I, получим выражение итоговой суммы S через P, r и t. S = P (1 + rt) (3) Так как для простого процента r всегда дается как годовая норма, время t должно измеряться в годах. Когда время дается в месяцах, t равно числу месяцев, поделенному на 12. Когда время дается в днях, используется два различных способа для подсчета t. Чаще используется деление числа дней на 360. Если t вычисляется таким способом, полученный процент называется обыкновенным простым процентом. Второй способ - использовать деление числа дней на 365 (366 в високосном году). Если t вычисляется таким образом, полученный процент называется точным простым процентом. ПРИМЕР 1 Найти простой процент за ссуду 3000 руб. на 5 месяцев при норме 0,07%. РЕШЕНИЕ Мы имеем P = 3000, r = 0,07 и t = 5/12. I = Prt = 3000 × 0,07 × (5/12) = 87,5 руб. ПРИМЕР 2. Н айти точный простой процент и итоговую сумму, если 5000 руб. даны взаймы на 100 дней при норме 4%. РЕШЕНИЕ P = 5000, r = 0,04 и t = 100/365 I = 5000 × 0,04 × (100/365) = 54,8 руб. S = 5000 + 54,8 = 5054,8 руб. ПРИМЕР 3 Человеку, который инвестировал 100000 руб., возмещены 101000 руб. девяносто днями позже. С какой нормой зарабатывались эти деньги при обыкновенном простом проценте? РЕШЕНИЕ P = 100000, S = 101000 и t = 90/360 = 1/4. Теперь, так как S = P + I, I = S - P = 101000 - 100000 = 1000. Но I = Prt, поэтому r = I/(Pt) = 1000/(100000 × (1/4)) = 0,04 = 4%. ПРИМЕР 4 Через 60 дней после займа Иванов выплатил ровно 10000 руб. Сколько было занято, если 10000 руб. включают основную сумму и обыкновенный простой процент при 12%? РЕШЕНИЕ S = 10000, r = 0,12 и t = 60/360 = 1/6. Подставляя эти значения в S = P(1 + rt), получим 10000 = P × (1,02) откуда P = 10000/ 1,02 = 9804 руб. Для вычисления простых процентов без использования современной вычислительной техники применяются различные практические приемы. Наиболее известный из них - шести процентный способ, который основан на том, что на каждый рубль при норме 6% обыкновенный простой процент за 60 дней равен 0,01 руб. Теперь, приводя реальную норму к 6% и реальный период к 60 дням для определения обыкновенного простого процента достаточно перемножить эти приведенные величины и полученное произведение умножить на один процент от основной суммы. Полученный результат и будет обыкновенным простым процентом. Кроме этого для определения простых процентов не прибегая к вычислениям, используются таблицы. В финансовой математике часто можно решать поставленную задачу несколькими методами. В этих условиях всегда следует искать наиболее простой способ, который сократит и ваш труд и риск числовых ошибок. Решение задач несколькими способами часто является желательным с целью проверки результата. УПРАЖНЕНИЯ 1 (В этих и всех последующих упражнениях, когда результат не выражается целыми числами, вычисления производить с точностью до второго десятичного знака после запятой, если в условиях не оговорено другое.) 1. Выразить следующие проценты в виде соответствующих натуральных и десятичных дробей с точностью до четвертого десятичного знака: a) 4 %, b) 2 1/4 %, c) 3&2 %, d) 3 1/3 %, e) 0,8 %, f) 1/6 %. 2. Представить каждую из следующих дробей в виде процентов с точностью до сотой доли процента; a) 0,035, b) 3/40, c) 0,04 (1/3), d) 5/16, e) 8,40/280, f) 40/1250. 3. Найти значения 1 + rt и выразить результат в виде натуральных и десятичных дробей: a) r = 6%, t = 1/2; b) r = 1 1/4 %, t = 1/3; c) r = 5%, t = 3/4; d) r = 3.2, t = 1/12; e) r = 3.2%, t = 1/8. 4. Вычислить (1 + 0,07(7/12))5000 руб. с точностью до 1 руб. 5. Найти простой процент для 7000 руб. за 5 месяцев при 3%. 6. Вычислить 6000рб/(1 + 0,05(1/4)) с точностью до 1 руб. 7. Найти простой процент и итоговую сумму, если 7000 руб. инвестируются на 4 месяца при 6 1/3 %. 8. Найти обыкновенный и точный простой процент для 4600 руб. за 120 дней при 7% в обычном году. 9. Найти обыкновенный простой процент и итоговую сумму для 150000 руб. при 5 1/4 % за 90 дней. 10. Банк начисляет 5 руб. обыкновенного простого процента за использование 300 руб. в течение 60 дней. Какова норма простого процента таких сделок? 11. При приобретении товаров покупатель может заплатить или 500 руб. сразу или 520 руб. через 4 недели. Если он займет деньги, чтобы заплатить наличными, какая норма простого процента u1084 может быть допустима для возмещения займа? 12. Найти P если S = 4800 руб., r = 7% и t = 1/4. 13. Найти S если P = 7000 руб., r = 8% и t = 1/6. 14. Какая основная сумма приведет к итогу 7800 руб. за 5 месяцев, если норма процента равна 8%? 15. Какая основная сумма приведет к итогу 13900 руб. через 90 дней при норме 8% обыкновенного простого процента? 16. Сколько дней понадобится, чтобы 7000 руб. заработали 100 руб., если они инвестируются при 9% обыкновенного простого процента? Найти точный и обыкновенный простые проценты: 17. P = 28000, r = 7%, t = 189 дней. 18. P = 96800, r = 6%, t = 227 дней. 19. P = 69500, r = 4,5%, t = 95 дней. 20. P = 18700, r = 12%, t = 128 дней.
2.3 ВРЕМЯ МЕЖДУ ДАТАМИ. ОФОРМЛЕНИЕ ВЕКСЕЛЕЙ Когда временной интервал дается не явно, а в форме промежутка между датами, обычно вычисляют точное число дней, включая первый или последний день, но не оба. Такой способ определяет так называемое точное время. Его легко определить, если обе даты относятся к одному и тому же году и имеется в наличии календарь, показывающий порядковый номер каждого дня года. Тогда достаточно из порядкового номера поздней даты вычесть порядковый номер ранней даты и результат даст продолжительность периода. В високосных годах порядковый номер дня после 28 февраля следует увеличивать на единицу. Упомянутый здесь календарь порядковых номеров дней года обычно содержится среди таблиц для финансовых расчетов, имеющихся в руководствах по финансовым и коммерческим расчетам. Другой способ подсчета количества дней между датами основан на предположении, что каждый месяц года состоит из 30 дней. Когда используется этот способ, получающийся результат называется приближенным временем. Независимо от того, каким образом рассчитывалось число дней временного периода, могут начисляться обыкновенные или точные простые проценты. Поэтому возможны четыре различных варианта числового выражения простого процента. Сочетание точного времени и точного простого процента практически не встречается. Чаще всего встречается случай, когда используется точное время и обыкновенный простой процент. Этот вариант часто называется правилом банкиров. В дальнейшем мы будем всегда подразумевать именно этот способ расчетов, если не будет оговорено другое. ПРИМЕР 1 Ссуда была выдана 10 марта и возвращена 17 ноября. Найти a) точное время, b) приближенное время периода. РЕШЕНИЕ a) 10 марта является 69-ым днем года, а 17 ноября является 321-ым днем года. Так что число дней точного времени равно 321 - 69 = 252. b) При определении приближенного времени для удобства составим следующую табличку: Дата Месяц День 17 ноября 11 17 10 марта 3 10 Разность 8 7 Разность равна 8 месяцев и 7 дней или 247 дней, если считать, что в каждом месяце по 30 дней. ПРИМЕР 2 Ссуда была выдана 20 октября 2005 года и возмещена 15 июня 2007 года. Найти a) точное время, b) приближенное время периода. РЕШЕНИЕ a) 20 октября является 293-ым днем года, а 15 июня является 166-ым днем года. Определяемый период включает 365 - 293 = 72 дня 2005 года, 365 дней 2006 года и 166 дней 2007 года. Поэтому точное время периода равно 72 + 365 + 166 = 604 дня. b) При определении приближенного времени опять обращаемся к использованию вспомогательной таблицы Дата Год Месяц День 15 июня 2007 6 15 15 июня 2006 18 15 15 июня 2005 17 45 20 октября 2004 10 20 Разность 1 7 25 Приближенное время периода равно 1 год 7 месяцев и 25 дней или 360 + 210 + 25 = 595 дней. Оформление денежных отношений между партнерами финансовой сделки может производиться при помощи векселей (расписок), которые, по существу, являются письменными обязательствами заплатить определенную сумму денег в установленный срок. Дата, до которой деньги должны быть выплачены, называется датой погашения. Сумма денег, которая должна быть выплачена, называется суммой погашения. Хотя эти две характеристики являются наиболее существенными, обычно в тексте расписки содержится и другая информация, которая может оказаться необходимой. Во всяком случае, текст векселя должен быть составлен таким образом, чтобы на его основании дата и сумма погашения могли бы быть однозначно определены. Например, предположим, что некто Иванов занял у Петрова 4000 руб. и согласился вернуть долг с 76 руб. процентов через 4 месяца. Тогда Иванов мог бы дать Петрову следующий вексель: **************************************************************** 10 октября 2007 г. Через четыре месяца после указанной даты я обязуюсь по требованию Петрова заплатить сумму 4000 руб. и простые проценты в размере 5,7% годовых. (Подпись) Иванов **************************************************************** Такой вексель является обязательством Иванова заплатить Петрову 4076 руб. 10 февраля 2008 г. Сумма 4000 руб. называется лицевой суммой векселя, а 4-месячный период называется сроком векселя. Другой вексель, эквивалентный по смыслу и значению, приведенному выше, выглядит так: **************************************************************** 10 октября 2007 г. Через четыре месяца после указанной даты по требованию Петрова я обязуюсь заплатить сумму 4076 руб. без процентов. (Подпись) Иванов ********************************************************** Когда срок векселя дан в месяцах, он обычно погашается в тот же самый день соответствующего месяца. Исключение составляет случай, когда дата погашения попадает на число месяца, которое не существует (например, 31 июня или 30 февраля). Тогда датой погашения считается последний день месяца. Если же срок векселя дан в днях, обычно рассчитывается точная дата выплаты занятых денег. Например, 80-дневный вексель, датированный 16 ноября, погашался бы 4 февраля. При таких расчетах снова был бы полезен календарь с порядковыми номерами дней года. ПРИМЕР 3 Установить дату погашения 60-дневной расписки, датированной 17 июля 2007 г. РЕШЕНИЕ 17 июля является 198-ым днем года. Добавляя 60 дней, получим 258-ой день года, которым является 15 сентября. Это и есть дата погашения.
2.4 ПРОСТОЙ ДИСКОНТ Дисконтом называют уменьшение суммы счета, расчета, долга и т.п. по какой либо причине. В математике финансов дисконтом является величина, вычитаемая из суммы погашения обязательства, когда обязательство принимается до даты его погашения. Сумма, остающаяся после вычитания дисконта из суммы погашения, называется выручкой. Например, предположим, что Иванов получил вексель от Петрова на 10000 руб., которые будут погашены через 5 месяцев. После этого Иванов продает этот u1074 вексель Сидорову за 9500. В этом случае дисконт равен 500 руб. и выручка равна 9500 руб. Нормой дисконта для данного периода времени называется отношение дисконта за период к сумме погашения. Как и в случае простого процента, эта норма всегда дается в процентах или эквивалентных десятичных дробях и обычно рассчитывается на годовой основе. Пусть S обозначает сумму погашения, d - норма дисконта за 1 год и t - продолжительность периода времени в годах. Если дисконт вычисляется по формуле D = Sdt, (4) он называется простым дисконтом или, банковским дисконтом. Если P обозначает выручку, тогда P = S - D. (5) Для простого или банковского дисконта равенства (4) и (5) играют ту же самую роль, какую играют равенства (1) и (2) для простого процента. Если из (4) и (5) исключить D, получается выражение для выручки через величины S, d и t: P = S (1 - dt). (6) Когда инвестор (в нашем примере Сидоров) покупает вексель до его даты погашения, он, по существу, ссужает деньги продавцу. То есть Сидоров практически ссудил Иванову 9500 руб. на 5 месяцев и владеет векселем Петрова как ценной бумагой. В день погашения Сидоров получит от Петрова 10000 руб., так что Сидоров получит 500 руб. прибыли за инвестицию 9500 руб. на 5 месяцев. Понятно, что 500 руб. могут рассматриваться как простой процент за инвестированные 9500 руб. Таким образом, в день погашения дисконт на S становится процентом на P. Или по-другому, S - P может рассматриваться или как дисконт на S или как процент на P. Ясно, что норма дисконта и норма процента не будут одинаковыми. В рассмотренном примере норма дисконта равна (из D = Sdt) d = D/(St) = 500/(10000 × (5/12)) = 0,12, в то время как норма процента равна (из I = Prt) r = I/(Pt) = 500/(9500 × (5/12)) = 12/95. Соотношение между нормой процента и нормой дисконта легко получается приравниванием правых частей равенств (1) и (4) и делением на t. Это дает Pr = Sd. (7) Ошибки в задачах, касающихся дисконта, обычно появляются из-за перепутывания норм r и d. Равенство (7) ясно показывает, что они не одинаковы и не являются взаимозаменяемыми. Когда вексель покупается до даты его погашения, цена P, которую инвестор будет платить, обычно определяется одним из двух следующих способов: a) Инвестор может установить, что используется данная норма дисконта d. В этом случае S, t и d известны и для нахождения P используется уравнение простого дисконта, P = S(1 - dt). b) Инвестор может установить норму процента r, которую он хотел бы реализовать за свою инвестицию. В этом случае S, t и r являются известными, так что для нахождения P должно быть использовано уравнение простого процента. Поэтому P = S/(1 + rt). Когда выручка от продажи векселя найдена одним из описанных способов, говорят, что вексель дисконтирован. Если используется способ a) дисконт называется банковским дисконтом или дисконтом по норме дисконта. Если используется способ b), дисконт называется дисконтом по норме процента или иногда истинным дисконтом. Когда человек занимает деньги и дает свой вексель, по существу, он продает свой вексель на время до даты погашения. В примере предыдущего параграфа Иванов фактически продал Петрову за 4000 руб. расписку о том, что через 4 месяца он выкупит ее за 4076 руб. 4000 руб. являются выручкой. 76 руб. можно рассматривать как дисконт от суммы погашения 4076 руб. 4 месяца спустя, когда Иванов возместит 4076 руб., 76 руб. будут процентом для Петрова за его инвестицию 4000 руб. на 4 месяца. Многие банки используют норму дисконта при выдаче любых ссуд. Однако при этом часто используется термин процент авансом в том же самом смысле, что и банковский дисконт. Например, Сидоров попросил ссуду 120000 руб. на 60 дней в банке, который использует 7% - ную норму процента авансом. В банке вычисляют величину процента авансом по формуле D = Sdt, где S = 120000, d = 0,07 и t = 1/6, получая значение 1400 руб., и выдают Сидорову 118600 руб., являющиеся выручкой от ссуды. Понятно, что вексель Сидорова о возмещении 120000 руб. через два месяца дисконтируется по способу a). Таким образом, термин процент авансом является синонимом банковского дисконта, а норма процента авансом является банковской терминологией нормы дисконта. ПРИМЕР 1 16 ноября 2007 Иванов продал сберегательному банку следующий вексель ******************************************************** 9 февраля 2007 Через год после указанной даты я обязуюсь выплатить по требованию Иванова 150000 руб. и простой процент 6% годовых. Подпись Петров **************************************************************** Если сберегательный банк использует 7% - ную норму процента авансом, a) какой будет выручка, b) какую норму процента реализует банк при такой инвестиции? РЕШЕНИЕ a) Вексель погашается 9 февраля 2007 г. за 159000 руб. С 16 ноября 2007 г. по 9 февраля 2007 г. пройдет 85 дней, так что S = 159000, t = 85/360 = 17/72, d = 0,07. D = Sdt = 159000 × 0,07 × (17/72) = 2627,92 руб., P = S - D = 159000 - 2627,92 = 156372,08 руб. b) P = 156372,08, t = 17/72 и I = 2627,92. Из равенства (1) I = Prt имеем r = I/Pt = 2627,92/(156372,08 × (17/72)) = 0,0712. ПРИМЕР 2 Вексель на 10175 руб., погашаемый через 90 дней, продан банку, который установил 7%-ную норму простого процента при дисконтировании. Какой будет выручка? РЕШЕНИЕ. З десь S = 10175 руб., t = 90/360 = 1/4 и r = 0,07. По формуле (3) S = P(1 + rt) получаем P = S/(1 + rt) = 10175/(1 + (0,07 × (1/4)) = 10000 руб. ПРИМЕР 3 Иванов намеревается получить ссуду в сберегательном банке на 120 дней. Если банк начисляет 7% процента авансом, какую сумму должен просить Иванов, чтобы получить на руки 100000 руб.? РЕШЕНИЕ Нам нужно определить S, имея следующие данные P = 100000 руб., t = 120/360 = 1/3 и d = 0,07. Из формулы (6) имеем P = S ( 1 - dt), что дает S = P /(1 - dt) = 100000/(1 - (0,07 × (1/4))) = 101781,17. Простой дисконт, так же как простой процент, обычно используется только для краткосрочных периодов, как правило, не превышающих года. Чаще применяется норма дисконта d, хотя большое расхождение терминологии в различных текстах и финансовых учреждениях затрудняет временами понять, какая норма упоминается норма процента r или норма дисконта d. В последующем тексте процент авансом означает банковский дисконт и его не следует путать с процентом, который всегда рассчитывается на P и выплачивается в конце сделки. УПРАЖНЕНИЯ 1.2 1. S = 170000 руб., d = 5%, период - два месяца. Найти D и P. 2. S = 250000 руб., d = 7%, период от 15 мая до 26 июля. Найти D и P. 3. P = 250000 руб., d = 7%, период от 15 мая до 26 июля. Найти D и S. 4. Вексель с суммой погашения 100000 руб. продан при норме дисконта 3,5% за 75 дней до даты погашения. Найти дисконт и выручку. 5. Найти выручку в условиях предыдущей задачи, если вместо нормы дисконта дана норма процента 3,5%. 6. Вексель с суммой погашения 60000 руб. 15 августа продан за 590000 руб. 16 июня. Какая норма дисконта была использована? Какую норму процента реализовал покупатель в результате сделки? 7. При получении товара торговец подписал вексель, обязуясь заплатить 240 млн. руб. через 60 дней. Найти выручку, если поставщик продает вексель банку, который использует 6,5%-ную норму дисконта. Какую прибыль получит поставщик, если товар стоит 190 млн. руб.? 8. Инвестор ссудил 34 млн. руб. и получил вексель с обязательством заплатить эту сумму плюс 7% простых процентов через 90 дней. Вексель был немедленно продан банку, который начисляет 6% банковского дисконта. Сколько заплатил банк за вексель? Какова прибыль инвестора? Какую норму процента реализует банк при погашении векселя? 9. Банк заплатил 44000 руб. за вексель с суммой погашения 45000 руб. через 4 месяца. Какова норма дисконта? Какова норма процента? 10.В векселе содержится обязательство выплатить 600000 руб. и обыкновенный простой процент при норме 5,5% через 60 дней. Он был дисконтирован при 6% банковского дисконта за 20 дней до погашения. Найти сумму погашения векселя и выручку от продажи. 11. 1 апреля 2007 г. Через 150 дней после указанной даты я обязуюсь заплатить Иванову 275000 руб. и обыкновенный простой процент при 6% годовых. Подпись Петров Найти сумму погашения и дату погашения. Если расписка продана 31 мая 2007 г. при 5% банковского дисконта, найти выручку. 12. 1 июня 2007 г. Я Иванов обязуюсь выплатить Петрову ровно 10000 руб. через 60 дней после указанной выше даты. Иванов 1 июня, когда Иванов подписал вексель, он получил 9500 руб. Какую процентную ставку обыкновенного простого процента установил Петров? Какая норма банковского дисконта дала бы такой же результат? 13.Просьба ссудить 50000 руб. на 4 месяца поступила в банк, который начисляет 8% процента авансом. Определить дисконт. Чему равна выручка ссуды? 14.Для того чтобы получить выручку 80000 руб., сколько нужно попросить в банке для 8-месячной ссуды, если банк начисляет 7% -ный банковский дисконт?
2.5 СОСТАВНОЙ ИТОГ И СЛОЖНЫЕ ПРОЦЕНТЫ Когда процент периодически добавляется к основной сумме и эта новая сумма используется, как основная для следующего временного периода и эта процедура повторяется определенное число периодов, окончательный итог называется составным итогом. Разность между составным итогом и первоначальной основной суммой называется сложным процентом. Период времени между двумя последовательными начислениями процентов называется периодом начисления процентов или периодом конверсии и может быть установлен любой удобной временной продолжительности. В качестве периода конверсии обычно берется целый делитель года, такой как месяц, квартал, 6 месяцев или год. Норма процента обычно рассчитывается на годовой основе и при начислении процентов должна изменяться до нормы процента на период инверсии. ПРИМЕР Найти составной итог в конце 1 года при основной сумме 50000 руб., если при начислении используется норма процента 7%, конвертируемая поквартально. РЕШЕНИЕ Слова 7%, конвертируемые (или составляемые) поквартально, означают 1,75% за квартал (3 месяца). Таким образом, в конце первого квартала 1,75% от 50000 руб. добавляются к основной сумме, увеличивая ее до итоговой суммы первого периода 50875 руб. Эта сумма является основной для второго периода. В конце второго квартала к ней добавляются 1,75% от 50875 руб., давая новый итог 51765,31 руб. в конце второго периода и основную сумму для третьего периода. В конце третьего периода к основной сумме этого периода добавляются 1,75% от 51765,31 руб. процентов третьего периода, приводя к итоговой сумме 52671,20 руб. третьего квартала. И, наконец, в конце года ,75% от 52671,20 руб. добавляются к основной сумме четвертого квартала, образуя составной итог года (четырех квартальных периодов) 53592,95 руб. Сложный процент за год равен 3592,95 руб., что на 92,95 руб. больше суммы, которая получилась бы при использовании простого процента. Прямой метод начисления процентов по периодам конверсии, использованный в примере, является утомительным, когда число периодов становится больше. Поэтому имеет смысл сформулировать более быстрые способы получения итоговой суммы, одинаково удобные для произвольного числа периодов конверсии. 2.6 ОБОЗНАЧЕНИЯ Будем использовать следующие обозначения: P - первоначальная основная сумма или настоящая стоимость S. S - составной итог для P, или итог на конец срока. n - количество процентных периодов (периодов конверсии). m - количество периодов конверсии за 1 год. j - норма процента, которая конвертируется m раз в году. i - норма процента за период конверсии: всегда i = j/m. Годовая норма j называется годовой номинальной нормой (ставкой) или более кратко номинальной ставкой, так как она является нормой, используемой только в рассматриваемой сделке. Норма i = j/m всегда используется при начислении итоговой суммы. Обычно используются следующие версии обозначений номинальной ставки, которые поясним примером: j = 0,15 или (15%, m = 3) или (j = 15%, m = 3) означают, что годовая номинальная норма 15% конвертируется 3 раза в год и что i = 0,05 является нормой процента за 4-месячный период. ПРИМЕР Найти приближенное значение итоговой суммы при накоплении процентов основной суммы 10000 руб. в течение 20 лет при норме процента i = 5,2%. РЕШЕНИЕ Из таблицы для множителей накопления имеем: i 0,055 0,050 (1 + i) 20 2,9178 2,6533 В этом случае i 1 = 0,050, i = 0,052, i 2 = 0,055. (i 2 - i)/(i 2 - i 1) = 3/5 = 0,6. (i - i 1)/(i 2 - i 1) = 2/5 = 0,4. Поэтому приближенное значение X величины (1 + 0,052)20 вычисляется следующим образом: X = (0,6)(2,6533) + (0,4)(2,9178) = 2,7591 Таким образом, итоговая сумма S приблизительно равна S = 10000 × 2,7591 = 27591 руб. Когда необходимо найти множитель накопления для значений i и n, которых в таблице нет, приходится вычислять этот множитель непосредственно. При этом удобно вычислить сначала логарифм множителя накопления по формуле: log(1 + i) п = n log(1 + i). В предыдущем примере это привело бы к результату log(1 + 0,052) = 20 log(1,052) = 20 × 0,0693 = 1,0139 что дает величину множителя накопления равную 2,7562 и итоговую сумму 27562 руб. Этот результат показывает, в частности, точность вычисления по приближенной формуле. Погрешность составляет 29 руб., то есть 0,00105 или 0,105% от итоговой суммы. В заключение заметим, что интерполяция является достаточно громоздкой процедурой и ею следует пользоваться только в тех случаях, когда под рукой есть таблицы и нет калькулятора, который мог бы возводить числа в произвольную степень. Если таковой имеется, лучше не использовать таблицы, а вычислять итоговую сумму по формуле (1). 2.7 НАСТОЯЩАЯ СТОИМОСТЬ И СЛОЖНЫЙ ДИСКОНТ Часто необходимо знать, какая основная сумма P, инвестированная теперь, при данной норме процента даст накопление до заданной итоговой суммы S к заданной более поздней дате. В этих условиях P называется настоящей стоимостью суммы S. Другими словами, настоящая стоимость P на данную дату для суммы S на более позднюю дату является основной суммой, которая, будучи инвестированной в данную дату при заданной норме процента, даст итог S в эту более позднюю дату. Разность S - P называется сложным дисконтом от о1089 суммы S, а процесс определения настоящей стоимости называется дисконтированием. Вычисление настоящей стоимости (или дисконтирование суммы S) означает просто решение уравнения (1) относительно P, когда S, i и n заданы. Решение уравнения (1) дает P = S/( 1 + i) п = S( 1 + i) -п. (2) Стоящий в знаменателе множитель накопления может быть вычислен способами, описанными в предыдущем параграфе. Тем не менее и в этом случае в руководствах по финансовым расчетам приводятся таблицы обратных значений множителей накопления (1 + i) - п, которые принято называть множителями дисконтирования.
Задания, исходные данные и методические указания по выполнению Домашней контрольной работы
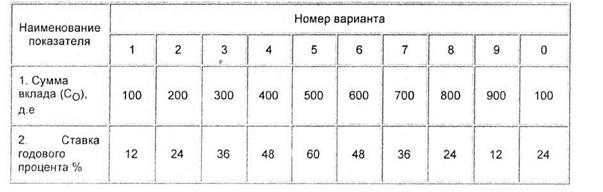
Самостоятельная практическая работа по дисциплине «Финансовый менеджмент» содержит задачи, теоретические вопросы и выполняется в соответствии с настоящими методическими указаниями. Целью самостоятельной практической работы является закрепление теоретических знаний слушателей в области финансово-кредитных отношений и получение практических навыков по осуществлению финансовых расчетов. Самостоятельная практическая работа включает следующие задания: Задание №1 "Определение временной ценности денег" Задание №2 "Оценка доходности финансовых активов (на примере акции)" Задание №3 "Оценка доходности финансовых активов (на примере облигации)" Задание №4 "Составление плана погашения кредита" Задание №5 "Изложение теоретических знаний по одной из тем дисциплин" Выполнение первых четырех заданий самостоятельной практической работы предполагает проведение расчетов по индивидуальным исходным данным, которые задаются согласно номеру варианта. При выборе темы, рассматриваемой в пятом задании самостоятельной практической работы, могут быть использованы два варианта: первый вариант - тема выбирается по номеру своего варианта, второй - тема выбирается студентом самостоятельно. Выбор варианта по последней цифре студенческого билета. Ознакомьтесь внимательно с исходными данными, заданием и методическими указаниями по выполнению заданий самостоятельной практической работы. Задание №1 "Определение временной ценности денег" Задание и исход ные данные. В коммерческий банк помещается сумма Cq на пять лет. Ставка годового процента составляет г. Числовые значения суммы вклада и годовой процентной ставки по вариантам приведены в таблице. Таблица 1 - Числовые значения суммы вклада и годовой процентной ставки по вариантам.
Определить, какая сумма будет к концу каждого года на расчетном счете при использовании простой схемы начисления процентов и при использовании сложной схемы начисления процентов с периодом капитализации: А) год; Б) полугодие; В) квартал; Г) месяц Построить и проанализировать график изменения наращенной суммы при изменении длительности периода начисления процентов. При построении графика рассмотреть простую схему начисления процентов и сложную схему начисления процентов с периодом капитализации: год, полугодие, квартал, месяц. Методические указания. Наращенная сумма при использовании простой схемы начисления процентов определяется по формуле: Б= С0 (1+гхп), Где С0 - сумма вклада; r-годовая процентная ставка; n -длительность вклада, год. Наращенная сумма по схеме сложных процентов определяется по формуле: Б=С0(1+r)L, Где r- процентная ставка за период капитализации; L - количество периодов капитализации. Результаты расчета наращенной суммы по схемам сложных и простых процентов рекомендуется записать в таблицу 2. Таблица 2- Расчет наращенной суммы при использовании простой и сложной схем начисления процентов.
Данные, приведенные в таблице являются основой для построения графика.
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.028 с.) |

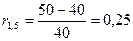 , или, что равносильно,
, или, что равносильно, 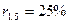 .
.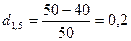 или
или 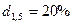
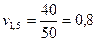 или
или 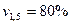 .
.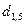 ,
, 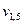 можно было найти, используя и другие соотношения. Например,
можно было найти, используя и другие соотношения. Например,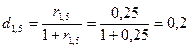 ;
;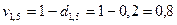 .
.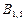 суммы кредита показывает, во сколько раз возвращаемая сумма больше выданной:
суммы кредита показывает, во сколько раз возвращаемая сумма больше выданной: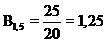 .
.